우선순위 큐(priority queue)

우선순위 큐

• pop 을 할때 우선순위가 가장 높은 원소가 먼저 나오는 큐

1. 원소의 추가 : O(log n)
2. 우선순위가 가장 높은 원소의 확인 : O(1)
3. 우선순위가 가장 높은 원소의 제거 : O(log n)
   => "힙(Heap)" 을 사용해서 구현함!

---

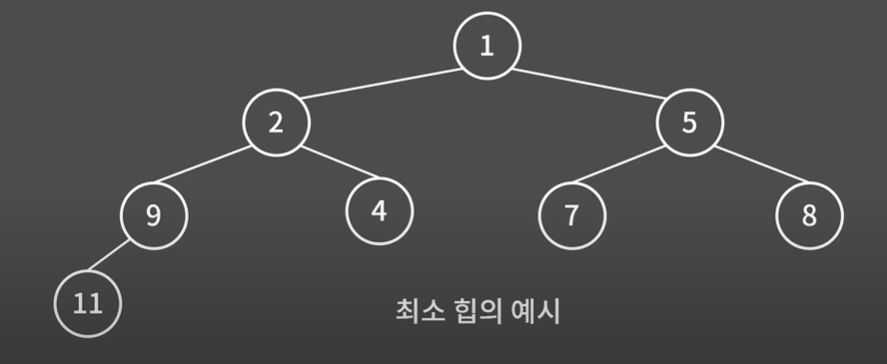
힙

• 이진트리로 구현
• 최대 힙 (max Heap) : 부모 key 값 < 자식 key 값
• 최소 힙 (min Heap) : 부모 key 값 > 자식 key 값

---

삽입 연산 (insert)

힙의 삽입 연산 : O(log n)

• 삽입 연산이 이루어지는 과정을 알아보자.

1. 힙(이진트리) 의 맨 좌측 끝 말단에다 새로운 노드를 삽입한다.
2. 힙의 순서조건을 위배하는지 검사한다. (최소힙일 경우 부모 key < 자식 key 라는 순서조건)
3. 업힙(Up - Heap) 을 수행한다.
   => 순서조건을 위배할 경우, 부모와 자식 노드의 위치를 서로 바꾼다.
   (=> 최악의 경우 : 힙의 높이만큼, 즉 O(log n) 만큼 루트 노드까지 올라가면서 위치를 바꾸는 경우)

---

최솟값 찾기 (Fetch) - 최소힙일때

• 최솟값이 위치한 노드 = 루트 노드
  => 루트 노드를 리턴하면 끝이다 => O(1)

• 반대로 최댓값을 찾는것은? => 최댓값을 가진 노드는 말단 노드(leaf node) 중에서 하나겠지만, 말단 노드들을 모두 일일이 다 확인하는 것은 힘들기도 하고 불가능하다고 보는게 좋다!

---

최솟값 삭제연산 (erase) - 최소힙일때

1. 루트 노드와 리프 노드의 가장 오른쪽 맨끝 노드를 서로 위치를 바꾼다.

2. 맨 마지막 위치로 이동한 노드 (기존 루트 노드) 를 삭제시킨다.

3. 다운힙(Down-Heap) 을 수행 => 순서 조건을 만족시키기 위해, 다운힙을 수행

(=> 흽의 높이만큼, 즉 O(log n) 만큼 다운힙을 수행)
==> 즉, 루트 노드 위치로 이동한 기존 리프 노드의 값을 순서 조건을 만족시키기 위해 게속 이동시킴!

---

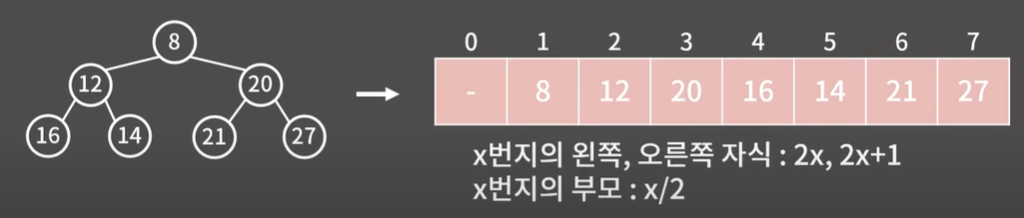
힙을 배열로 나타내기

• 부모의 인덱스를 i 라고할떄,
  왼쪽 자식의 인덱스 : 2i
  오른쪽 자식의 인덱스 : 2i + 1

---

힙 구현

#include <bits/stdc++.h>
using namespace std;

int heap[100005];
int sz = 0; // 힙에 들어있는 원소의 수

void push(int x){
	heap[sz++] = x;
	int idx = sz;
	while (idx != -1) {
		int par = idx / 2;
		if (heap[par] <= heap[idx])
			break;
		swap(heap[par], heap[idx]);
		idx = par;
	}
}

int top() {
	return heap[1];
}

void pop() {
	heap[1] = heap[sz--];
	int idx = 1;
	// 왼쪽 자식의 인덱스 ( = 2 * idx) 가 sz 보다 크면 idx 는 리프노드
	while (2 * idx <= sz) {
		int lc = 2 * idx, rc = 2 * idx + 1; // 왼쪽자식, 오른쪽자식
		int min_child = lc; // 두 자식 중 작은 인덱스를 담을 예정
		if (rc <= sz && heap[rc] < heap[lc])
			min_child = rc;
		if (heap[idx] <= heap[min_child])
			break;
		swap(heap[idx], heap[min_child]);
		idx = min_child;
	}
}

---

STL priority queue

#include <bits/stdc++.h>
using namespace std;

int main(void)
{
	priority_queue<int> pq; // 최대 힙
	// priority_queue<int, vector<int> greater<int>> 로 선언시 최소 힙

	// => greater : functional 헤더파일에 정의. 기본적으로 priority_queue 를 최대힙인데, greater<int> 를 인지로 주면
	// 대소관계가 뒤집혀서 최소힙으로 쓸수있다.

	pq.push(10);
	pq.push(2);
	pq.push(5);
	pq.push(9);

	cout << pq.top() << '\n';
	cout << pq.size() << '\n';

	if (pq.empty())
		cout << "pq is empty \n";
	else
		cout << "pq is not empty \n";

	pq.pop();  // {2, 5};

	cout << pq.top();
}

---

priority_queue VS set

• priority_queue 보다 set 이 기능하는 제공도 많고, 연산의 시간복잡도도 동일해서 set 을 쓰면 되지 않나? 라는 의문이 들수있다.

그러나 시간복잡도는 동일해도, priority_queue 가 2~4배 가량 더 동작속도가 빠르다.
따라서 priority_queue 에서만 제공되는 기능을 사용해도 되는 상황일 경우에는 priority_queue 를 사용하자!

---

Parametric Search

조건을 만족하는 최소/최댓값을 구하는 문제(최적화 문제) 를 결정문제로 변환해 이분탐색을 수행하는 방법