이번 포스팅에서는 하노이의 타워를 재귀로 구현하는 원리에 대해 알아보겠습니다.
현 포스팅 내용을 꼼꼼히 읽어보시고 확실하게 이해하시면 좋갰습니다. 재귀(Recursion) 의 호출 구조에 대한 원리를, 추후 어떤 문제를 직면했을때 재귀적인 구조를 어떻게 적용시킬지를 아실 수 있을겁니다.
하노이의 탑은 정말 중요한 문제라고 생각이듭니다. 이 문제를 완전히 자신의 것으로 만든다면, 정말 많은 것들을 얻어가고 재귀에 대한 새로운 관점이 보이실 겁니다.
재귀(Recursion) 에 대한 접근방식
우선 재귀에 대한 접근법은 특정 일정한 패턴을 찾아내는 것이 핵심입니다. 또 찾아낸 패턴을 바탕으로 귀납적 사고방식으로 문제를 접근해야 합니다. 재귀에 대한 내용은 인터넷의 자료를 참고하셔도 좋고, 제 알고리즘 포스팅을 참고하시며 이해하셔도 좋습니다.
하노이의 탑 : 조건

하노이의 탑은 기둥1에 n개의 원판이 주어졌을 때 기둥 3에다 해당 원판들을 모두 옮기는 것이 문제입니다. 이떄 아래와 같은 조건을 지키켜 옮겨야하느라 고생을 하죠.
쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.
절차지향적인 방식으로 접근을 했다면..?
저희는 절차지향적인 관점으로 재귀를 접근한다면 절대 문제를 해결할 수 없다는 것을 알고있습니다. 현재 하노이 탑에서 이 관점으로 접근을 해보자면, 아래와 같이 접근했을 겁니다.
원판이 3개가 있을때, 원판 3번을 기둥 3으로 옮기고, 원판 2번을 기둥 2로 옮기고,
원판 1번을 2번으로 옮기고, ...이 방식은 어찌어찌 많은 고민을 하며 원판의 개수가 3일때는 해결할 수 있을 겁니다. 그러나 원판의 개수가 4,5개만 되더라고 꽤 오랜 시간이 걸리며, 중간에 실수 한번만 하더라도 꼬이고 절대 해결하지 못할겁니다.
일정한 패턴을 찾아보자!
자, 이런 바보같은 사고방식이 아닌 더 창의적인 방식을 생각해봅시다.
이떄 바로 귀납적 사고방식을 통해 접근을 할 수 있겠죠?
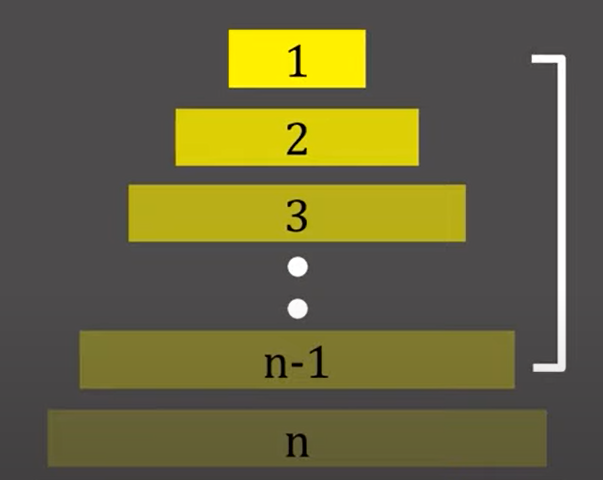
n번 원판이 3번기둥으로 이동하기위해선, 나머지 n-1개의 원판들이 전부 2번 기둥으로 비켜줘야 할겁니다.
왜냐하면 n-1 개의 원판들 중에서 어느 하나라도 기둥 3으로 가게된다면, 작은 원판위에 큰 원판을 둘 수 없는 규칙 떄문에 n번 원판을 3번 기둥으로 옮길수가 없게 되겠죠.
n-1 개의 원판들을 기둥 2번으로 이동시킨다면 아래와 같은 모습이 될 겁니다.
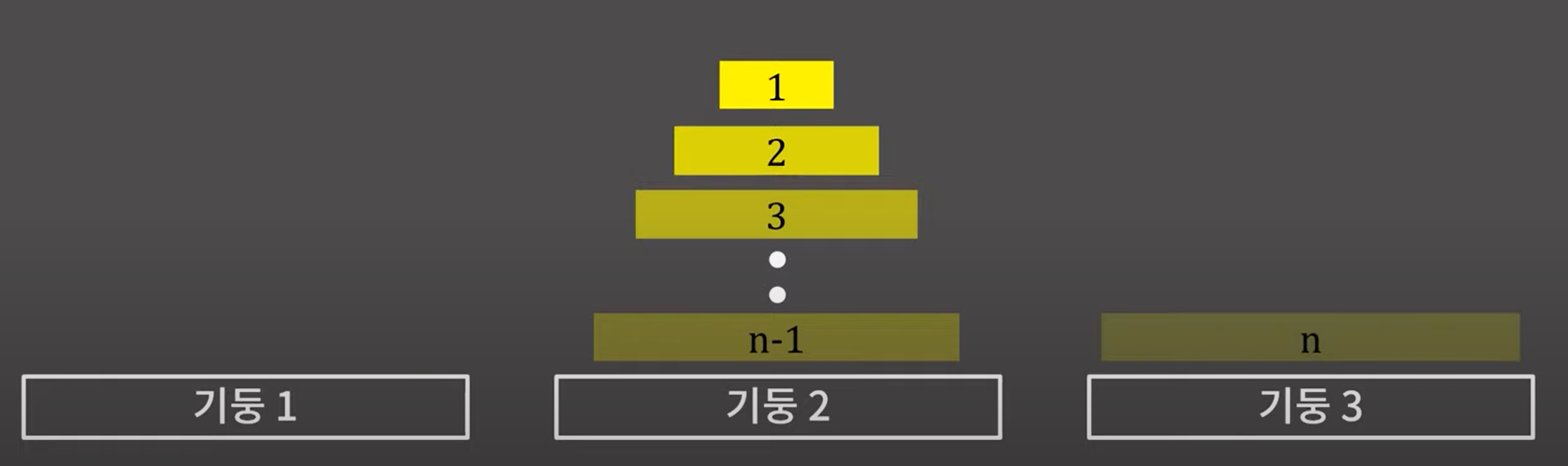
그리고 n번 원판을 기둥 3으로 옮기면 될 겁니다.

위 과정들을 통해 저희는 패턴을 찾아낸겁니다. 이를 정의해보자면 아래와 같습니다.
- 기둥1의 n-1개의 원판을 기둥 2로 옮긴다.
- n번째 원판을 기둥 3으로 옮긴다.
정의화
위에서 찾아낸 패턴을 구체적으로, 더 정확한 표현으로 정의화해봅시다.
우선 원판의 이동순서를 정의해봅시다.
- n-1개의 원판을 기둥 1에서 기둥 2로 옮긴다.
- n번 원판을 기둥 1에서 기둥 3으로 옮긴다.
- n-1개의 원판을 기둥 2에서 기둥 3으로 옮긴다.
위의 이동순서를 통해 저희는 아래와 같은 정의를 얻어낼 수 있습니다.
원판이 n-1개일때 옮길 수 있다면, 원판이 n개일때도 옮길 수 있다.
그리고 또 base condition 을 고려해보면 아래와 같은 관점도 생각해낼 수 있습니다.
원판이 1개일 때 원판을 내가 원하는 곳으로 옮길 수 있다.
원판이 k개일 때 옮길 수 있다면, 원판이 k+1 개일때도 옮길 수 있다.
이에 따라 이 문제를 귀납적으로 해결할 수 있음을 알게되었습니다.
함수의 정의
위에서 찾아낸 정의를 통해 저희는 재귀호출을 함수로써 표현해야 할겁니다.
함수를 정의해보면, 우선 아래와 같은 관점으로 생각해내서 정의해볼 수 있습니다.
void func(int n); => 원판 n개를 기둥 1에서 기둥 3으로 옮기는 방법을 출력하는 함수
하지만 이 함수에는 결함이 있습니다. func(n), 즉 원판 n개를 기둥 1에서 기둥 3으로 옮기려면 원판 n-1개를 기둥 1에서 기둥 3으로 기둥 2으로 옮겨야 할텐데, 함수가 이런 형태라면 활용이 불가능하겠죠? func(n-1) 을 활용할 수가 없는겁니다.
그러면 어떤 형태여야하는가?
라고 물었을때, 아래와 같은 함수로써 정의하면 됩니다.
void func(int a, int b, int n)원판 n개를 a번 기둥에서 b번 기둥으로 옮기는 방법을 출력하는 함수
Base Condition
base condition 은 n =1 일때 a에서 b로 옮기도록 하면 됩니다.
재귀 식
마지막으로 재귀식도 정의해봅시다. 일단 기둥의 번호는 6-a-b 입니다.
이제 원판 n개를 기둥 a에서 b로 옮기는 과정을 과정을 풀어쓰면 아래와 같습니다.
- n-1개의 원판을 기둥 a에서 기둥 6-a-b 로 옮긴다. // func(a, 6-a-b, n-1);
- n번 원판을 기둥 a에서 기둥 b로 옮긴다. // cout << a <<' '<< b << endl;
- n-1개의 원판을 기둥 6-a-b 에서 기둥 b로 옮긴다. // func(6-a-b, b, n-1);
// 원판 n개를 a번 기둥에서 b번 기둥으로 옮기는 방법을 출력하는 함수
void func(int a, int b, int n) {
if (n == 1) { // 원판이 1개일때는 a에서 b로 옮길 수 있다.
cout << a << ' ' << b << '\n';
return;
}
func(a, 6 - a - b, n - 1); // n-1개의 원판을 기둥 a에서 6-a-b로 옮기고
cout << a << ' ' << b << '\n'; // n번쨰 원판을 기둥 a에서 b로 옮긴다.
func(6-a-b, b, n - 1); // n-1 개의 원판을 기둥 6-a-b 에서 기둥 b로 옮긴다.
}