Disjoint set 이란?
Disjoint set은 서로 중복되지 않는 부분 집합들로 나누어진 원소들에 대한 정보를 저장하고 조작하는 자료구조이다.
집합을 구현하는 데는 비트벡터, 배열, 연결리스트, 트리 등을 이용할 수 있으나 그 중 가장 효율적인 트리구조를 이용하여 구현한다.
Disjoint Set의 연산
- make-set(x)
초기화 작업, x를 유일한 원소로 하는 새롤운 집합을 만든다.
- find(x)
x가 속한 집합의 대표값(루트 노드)을 반환한다. 즉, x가 어떤 집합에 속해 있는지 찾는 연산이다.
- union(x, y)
x가 속한 집합과 y가 속한 집합을 합친다.
Union-Find 코드
// 초기화
int parent[n];
for(int i = 0; i < n; i++)
parent[i] = i;
// find : 재귀 이용
int find(int u) {
// 루트 노드는 부모 노드 번호로 자기 자신을 가진다.
if(parent[u] == u)
return u;
// 각 노드의 부모 노드를 찾아 올라간다.
return find(parent[u]);
}
// union
void union(int xu int v) {
// 각 원소가 속한 트리의 루트 노드를 찾는다.
u = find(u);
v = find(v);
if(u != v) parent[v] = u;
}시간복잡도
-
find(x)
트리의 높이와 시간 복잡도가 동일하다.
최악의 경우 O(n - 1)이다. -
union(x, y)
find 연산이 전체 수행시간을 지배한다.
즉, 최악의 경우 O(n - 1)이다.
Disjoint set 최적화
위와 같이 구현할 경우, 최악의 경우 트리의 장점을 전혀 살릴 수 없는 연결 리스트 형태가 되면 Union과 Find 연산 모두 O(n)이 되어버릴 수 있다.
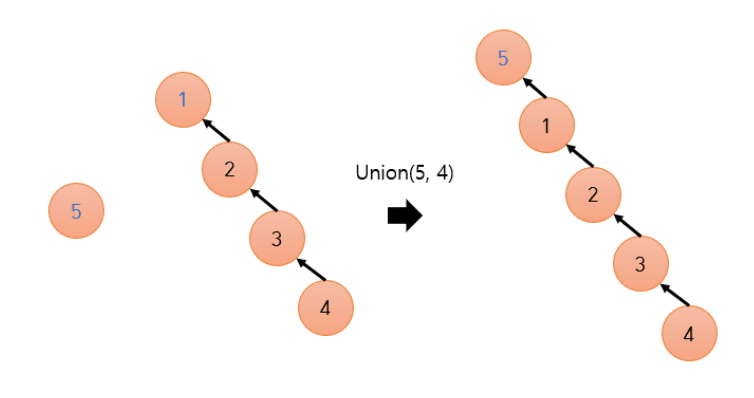
이 문제는 두 트리를 합칠 때, 항상 높이가 더 낮은 트리를 높은 트리 밑에 넣음으로써 해결할 수 있다. 이렇게 되면, 트리의 높이가 크게 높아지는 상황을 방지할 수 있다.
Union-Find 최적화 코드
🤚 최적화 원리
- find 연산에서 경로를 압축한다.
- rank에 트리의 높이를 저장하며 두 트리의 rank가 동일하여 높이가 높아져야만 하는 경우에는 union 후 결과 트리의 rank를 1 증가시킨다.
/* 초기화
int parent[n];
int rank[n];
for(int i = 0; i < n; i++)
parent[i] = i;
for(int i = 0;i < n; i++)
rank[i] = 1;
*/
int find(int u) {
if(u == parent[u])
return u;
// parent를 찾아낸 루트로 아예 바꿔버리면
// find 연산 수행시 중복되는 연산을 줄여준다.
// 재귀적인 구현 덕분에 u에서 루트까지 올라가는 경로상에 있는
// 모든 노드들에게도 경로 압축 최적화가 자동으로 수행된다.
return parent[u] = find(parent[u]);
}
void union(int u, int v) {
u = find(u);
v = find(v);
if(u == v) return;
if(rank[u] > rank[v])
swap(u, v);
parent[u] = v;
// 두 트리의 높이가 같은 경우에는 결과 트리의 rank를 1 증가시킨다.
if(rank[u] == rank[v]) rank[v]++;Union-Find 최적화 시간복잡도
👉 O(logN)
이 최적화 과정을 거치면 트리의 높이는 합쳐진 두 트리의 높이가 같을 때만 증가하게 된다.
즉, 최적화를 통해 트리의 높이가 포함한 노드의 수의 로그에 비례하는 것을 보장하게 되므로 union과 find의 연산의 시간복잡도가 O(logN)이 된다.