1. tree 구조

• 트리: node와 branch를 이용해서, 사이클을 이루지 않도록 구성한 데이터 구조
• 실제로 어디에 많이 사용되나?
  • 트리 중 이진 트리(binary tree)형태의 구졸, 탐색(검색) 알고리즘 구현을 위해 많이 사용됨

알아둘 용어

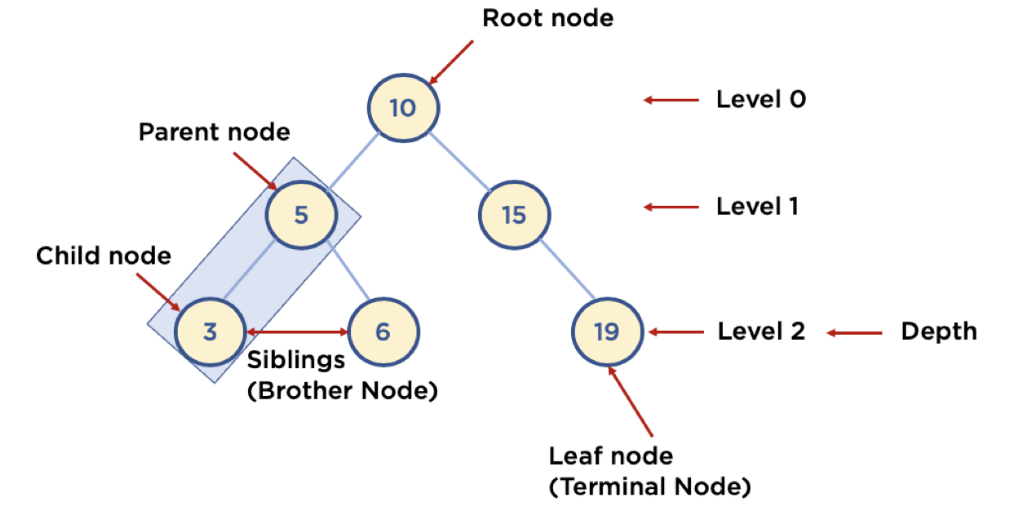
• node : 트리에서 데이터를 저장하는 기본 요소 (다른 연결 노드에 대한 branch 정보 포함)
• root node : 트리 맨 위에 있는 노드
• level : 최상위 노드를 level 0으로 하였을 때, 하위 branch로 연결된 노드의 깊이를 나타냄
• parenet node : 어떤 노드의 다음 레벨에 연결된 노드
• child node : 어떤 노드의 상위 레벨에 연결된 노드
• leaf node (=terminal node) : child node가 하나도 없는 노드
• sibling (brother node) : 동일한 parent node를 가진 노드
• depth : tree에서 node가 가질 수 있는 최대 level

이진 트리와 이진 탐색 트리 (Binary Search Tree)

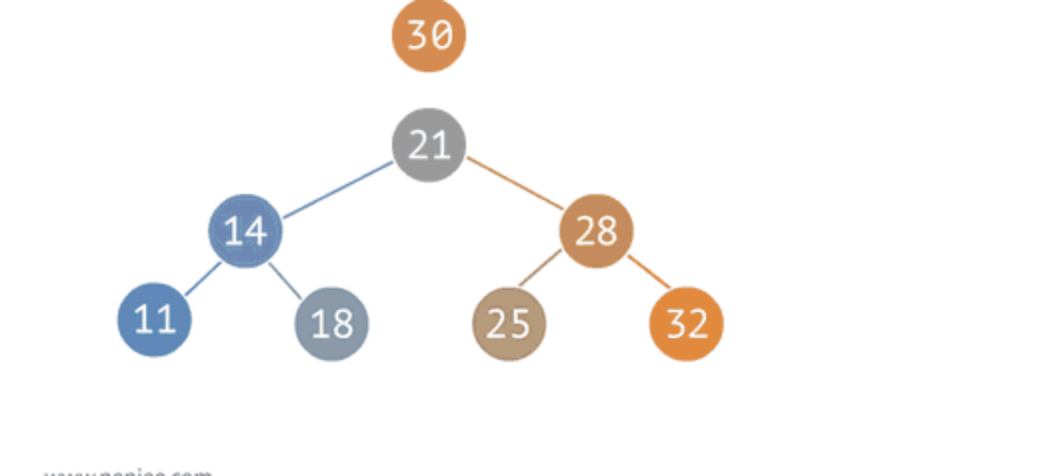
• 이진 트리 : 노드의 최대 branch가 2인 트리
• 이진 탐색 트리 (Binary Search Tree, BST) : 이진 트리에 다음과 같은 추가적인 조건이 있는 트리
  • 왼쪽 노드는 해당 노드보다 작은 값
  • 오른쪽 노드는 해당 노드보다 큰 값을 가지고 있음
  • 왼쪽 노드 < 해당 노드 < 오른쪽 노드

2. 자료 구조 이진 탐색 트리의 장점과 주요 용도

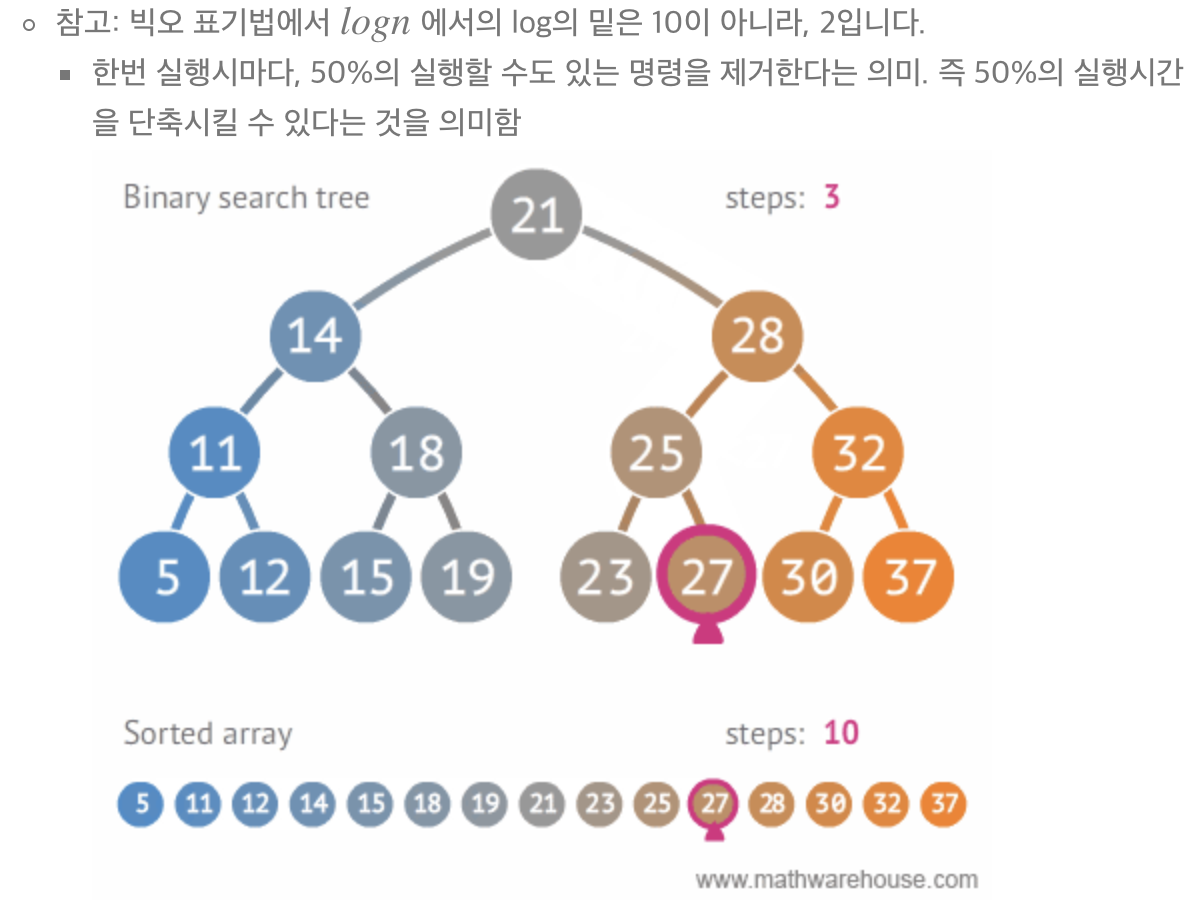
• 주요 용도 : 데이터 검색(탐색)
• 장점 : 탐색 속도를 개선할 수 있음

이진 트리와 정렬된 배열간의 탐색 비교

---

3. 파이썬 객체지향 프로그래밍으로 링크드 리스트 구현하기

3-1) "노드 클래스" 만들기

class Node:
    def __init__(self, value):
        self.value = value
        self.left, self.right = None, None

3-2) 이진 탐색 트리에 "데이터 넣기"

• 왼쪽 노드 < 해당 노드 < 오른쪽 노드

class NodeMgmt:
    def __init__(self, head):
        self.head = head
    
    def insert(self, value):
        self.current_node = self.head
        while True:
            if value < self.current_node.value:
                if self.current_node.left != None:
                    self.current_node = self.current_node.left
                else:
                    self.current_node.left = Node(value)
                    break
            else:
                if self.current_node.right != None:
                    self.current_node = self.current_node.right
                else:
                    self.current_node.right = Node(value)
                    break

head = Node(1)
binary_tree = NodeMgmt(head)
binary_tree.insert(2)

3-3) 이진 탐색 트리의 "탐색"

class NodeMgmt:
    def __init__(self, node):
        중간생략
    def insert(self, value):
        중간생략
    def search(self, value):
        self.current_node = self.head
        while self.current_node:
            if self.current_node.value == value:
                return True
            elif value < self.current_node.value:
                self.current_node = self.current_node.left
            else:
                self.current_node = self.current_node.right
        return False

head = Node(1)
binary_tree = NodeMgmt(head)
binary_tree.insert(2)
binary_tree.insert(0)
binary_tree.insert(4)
binary_tree.insert(8)
binary_tree.insert(-2)

binary_tree.search(8)

4. 이진 탐색 트리 삭제

• 매우 복잡함!
• 경우를 나누어 이해하는 것이 좋음
  • 1) leaf node 삭제 (child node 없음)
  • 2) child node가 하나인 node 삭제
  • 3) child node가 두개인 node 삭제

4-1) leaf node 삭제

• 삭제할 노드의 parent 노드가 삭제할 노드를 가리키지 않도록
  

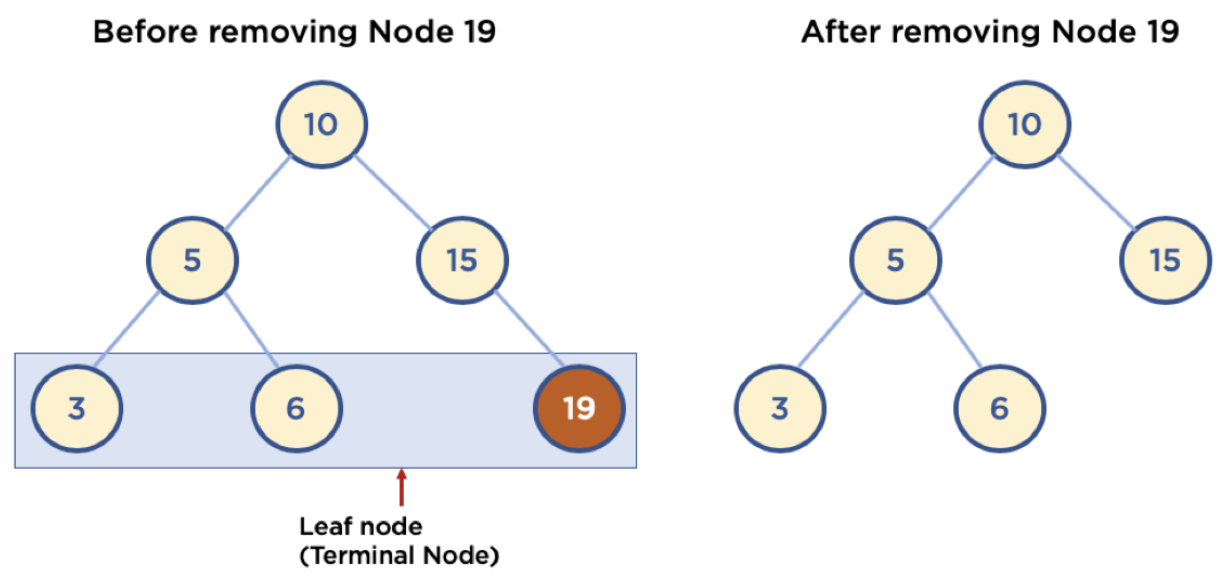
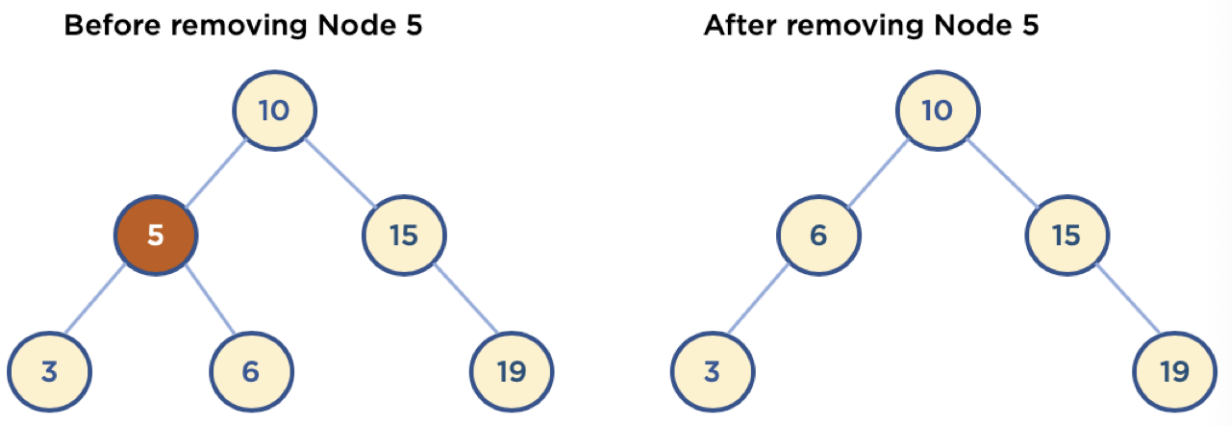
4-2) child node가 하나인 node 삭제

• 삭제할 node의 parent 노드가 삭제할 노드의 child 노드를 가리키도록 함
  

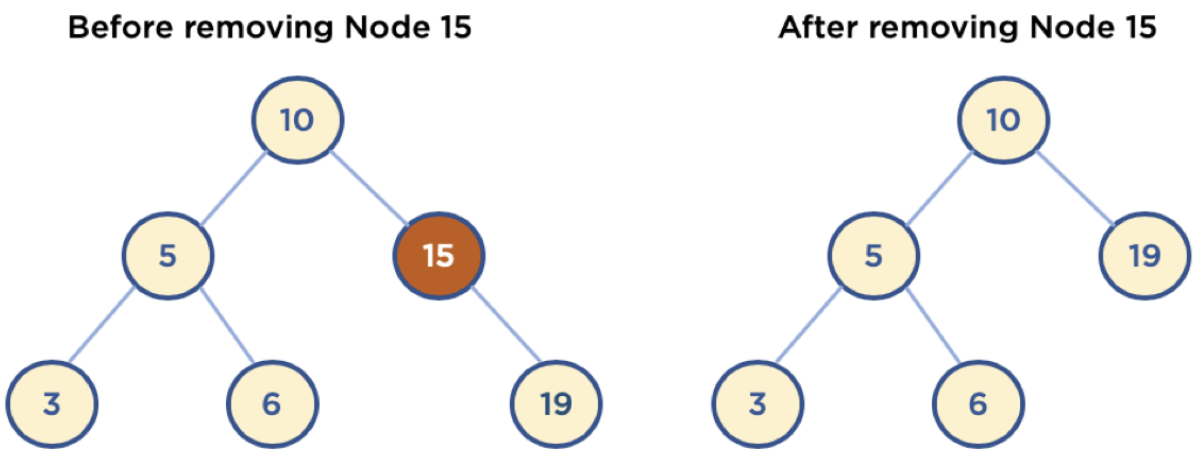
4-3) child node가 두 개인 node 삭제

• 방법#1: 삭제할 노드의 오른쪽 자식 중, 가장 작은 값을 삭제할 node의 parent 노드가 가리키도록
• 방법#2: 삭제할 노드의 왼족 자식 중, 가장 큰 값을 삭제할 노드의 parent 노드가 가리키도록
  

5. 이진 탐색 트리 삭제 코드 구현과 분석

삭제할 node 탐색

• 삭제할 노드가 없는 경우도 처리해야 함!
• 삭제할 노드가 없는 경우는 false를 리턴하고! 함수종료!

def delete(self, value):
    searched = False
    self.current_node, self.parent = self.head, self.head
    while self.current_node:
        if self.current_node.value == value:
            searched = True
            break
        elif value < self.current_node.value:
            self.parent = self.current_node
            self.current_node = self.current_node.left
        else:
            self.parent = self.current_node
            self.current_node = self.current_node.right
    if searched == False:
        return False

case#1 삭제할 노드가 leaf node인 경우

if self.current_node.left == None and self.current_node.right == None:
    if value < self.parent.value:
        self.parent.left = None
    else:
        self.parent.right = None

case#2 삭제할 노드가 child node를 한 개 가지고 있을 경우

# 삭제할 노드에 왼쪽 자식만 있는 경우
if self.current_node.left != None and self.current_node.right == None:
    if value < self.parent.value:
        self.parent.left = self.current_node.left
    else:
        self.parent.right = self.current_node.left

# 삭제할 노드에 오른쪽 자신만 있는 경우
elif self.current_node.left == None and self.current_node.right != None:
    if value < self.parent.value:
        self.parent.left = self.current_node.right
    else:
        self.parent.right = self.current_node.right

case#3 삭제할 노드가 child node를 두 개 가지고 있을 경우

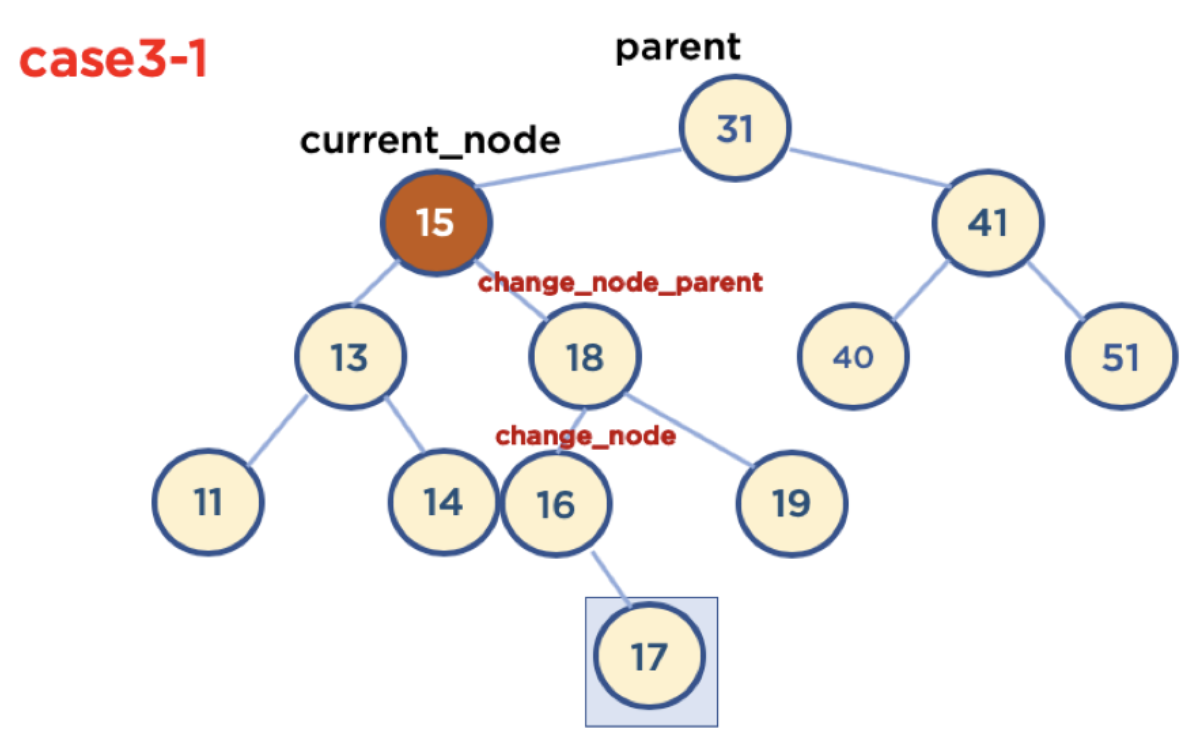
case#3-1 삭제할 노드가 parent node "왼쪽"에 있을 때

• 기본 사용 가능 전략

  • 전략#1: 삭제할 노드의 오른쪽 자식 중, 가장 작은 값을 삭제할 노드의 parent 노드가 기리키도록!
  • 전략#2: 삭제할 노드의 왼쪽 자식 중, 가장 큰 값을 삭제할 노드의 parent 노드가 가리키도록!

• 기본 사용 가능 전략 중, 1번 전략을 사용하여 코드를 구현하기로 함!

• 추가 고려해야하는 경우의 수 2가지:

  • case#3-1-1. 삭제할 노드가 parent 노드 왼쪽에 있고, 삭제할 노드의 오른쪽 자식 중, 가장 작은 값을 가진 노드의 child 노드가 없을 때
  • case#3-1-2. 삭제할 노드가 parent 노드 왼쪽에 있고, 삭제할 노드의 오른쪽 자식 중, 가장 작은 값을 가진 노드의 오른쪽 child 노드가 있을 때
    * 가장 작은 값을 가진 노드의 child 노드가 왼쪽에 있을 경우는 없음, 왜냐하면 왼쪽 노드가 있다는 것은 해당 노드보다 더 작은 값을 가진 노드가 있다는 뜻이기 때문

if self.current_node.left != None and self.current_node.right != None:
    if value < self.parent.value:
        self.change_node = self.current_node.right
        self.change_node_parent = self.current_node.right
        while self.change_node.left != None:
            self.change_node_parent = self.change_node
            self.change_node = self.change_node.left
        self.change_node_parent.left = None
        if self.change_node.right != None:
            self.change_node_parent.left = self.change_node.right
        else:
            self.change_node_parent.left = None
        self.parent.left = self.change_node
        self.change_node.right = self.change_node_parent
        self.change_node.left = self.current_node.left

case#3-2 삭제할 노드가 parent node 오른쪽에 있을 때

• 기본 사용 가능 전략
  • 전략#1: 삭제할 노드의 오른쪽 자식 중, 가장 작은 값을 삭제할 노드의 parent 노드가 가리키도록 함
  • 전략#2: 삭제할 노드의 왼쪽 자식 중, 가장 큰 값을 삭제할 노드의 parent 노드가 가리키도록 함
• 기본 사용 가능 전략 중, 1번 전략을 사용하여 코드를 구현하기로 함
• 경우의 수가 또다시 2가지가 있음:
  • Case#3-2-1: 삭제할 노드가 parent 노드의 왼쪽에 있고, 삭제할 노드의 오른쪽 자식 중, 가장 작은 값을 가진 노드의 child 노드가 없을 때
  • Case#3-2-2: 삭제할 노드가 parent 노드의 왼쪽에 있고, 삭제할 노드의 오른쪽 자식 중, 가장 작은 값을 가진 노드의 오른쪽에 child 노드가 있을 때
    • 가장 작은 값을 가진 노드의 child 노드가 왼쪽에 있을 경우는 없음, 왜냐하면 왼쪽 노드가 있다는 것은 해당 노드보다 더 작은 값을 가진 노드가 있다는 뜻이기 때문

else: # if self.parent.value < value
    self.change_node = self.current_node.right
    self.change_node_parent = self.current_node.right
    while self.change_node.left != None:
        self.change_node_parent = self.change_node
        self.change_node = self.change_node.left
    self.change_node_parent.left = None
    if self.change_node.right != None:
        self.change_node_parent.left = self.change_node.right
    else:
        self.change_node_parent.left = None
    
    self.parent.left = self.change_node
    self.change_node.right = self.change_node_parent
    self.change_node.left = self.current_node.left

6. 파이썬 전체 코드 구현

class Node:
    def __init__(self, value):
    

7. 파이썬 전체 코드 테스트

8. 이진 탐색 트리의 시간 복잡도와 단점

8-1) 시간 복잡도 (탐색시)

• depth(트리의 높이)를 h라고 표기한다면, O(h)
• n개의 노드를 가진다면, h = logn에 가까우므로, 시간복잡도는 O(logn)
  

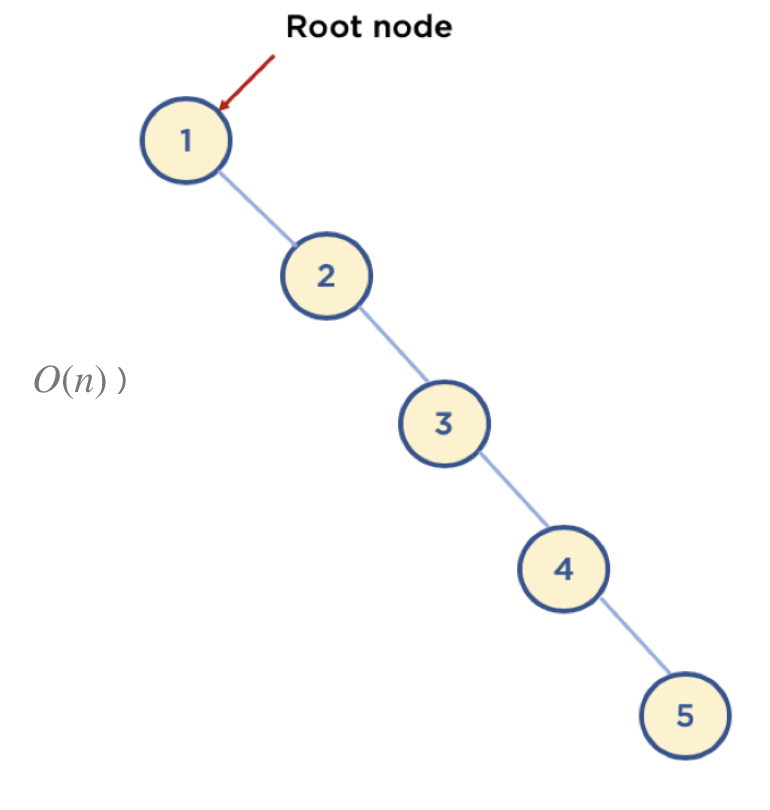
8-2) 이진 탐색 트리 단점

• 평균 시간 복잡도는 O(logn)이지만, 이는 트리가 균형잡혀있을 때!
• 아래와 같이 최악의 경우는, 링크드 리스트등과 동일한 성능(O(n))을 보여줌!
  

Reference

• 잔재미 코딩/대표적인 자료구조: 트리 (https://www.fun-coding.org/Chapter10-tree.html)