전통적인 강화학습 분야에서 model-free(MDP를 모르는 상황) 즉 전이확률과 보상함수에 대한 정보가 없을 때 Monte carlo, TD-Learning(temporal diffrence learning)을 사용한다.
해당 포스트는 TD-learning 기법 중 n-step TD와 backward TD()를 구현한다.
기본적으로 TD-learning은 샘플을 기반으로 state를 업데이트하는 방법이다.
one-step td learning은 (state, action, reward, next state) pair를 이용해 현재 state를 업데이트 한다. 즉 현재 상태에서 한번의 액션을 취하고 얻은 보상과 다음 상태에서의 value값을 통해 현재 state를 업데이트한다.
그러면 n-step td learning은 n번의 step을 이동하여 현재 state를 업데이트한다.
ex) 2-step: (state, action, reward, action, reward, next_state2)
수식으로 표현하면 아래와 같다
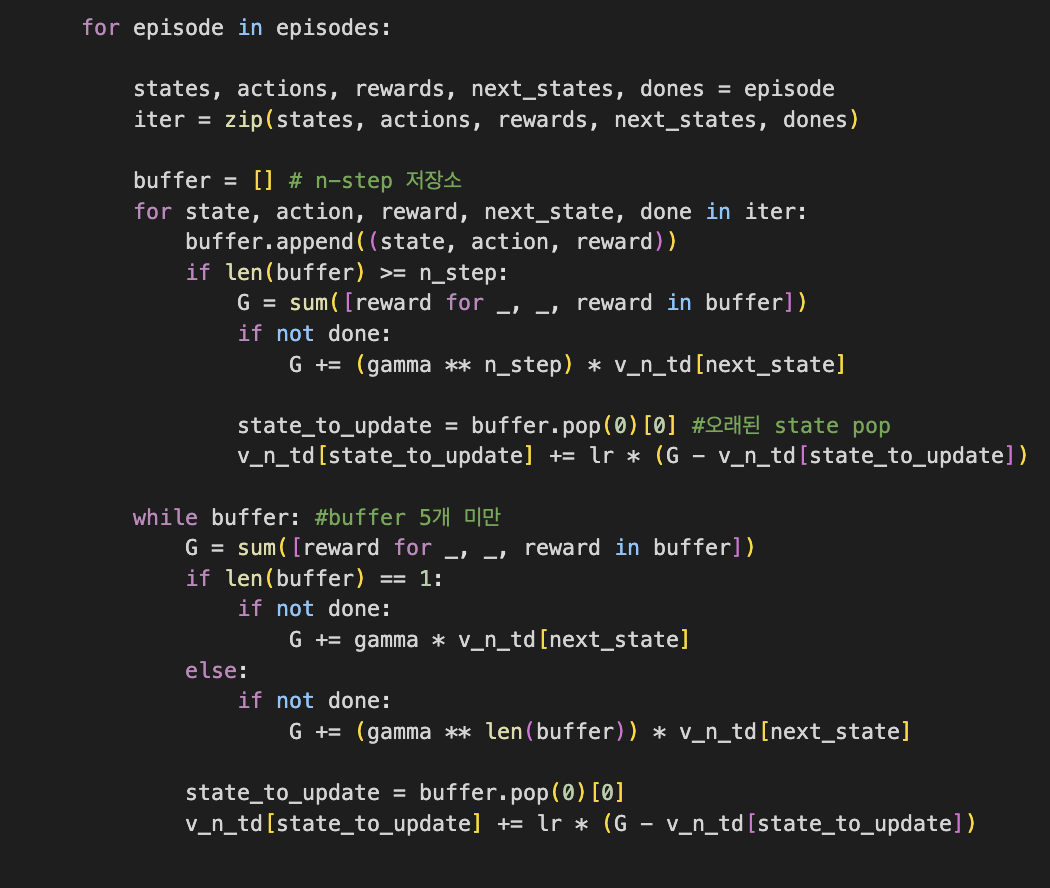
구현(5-step td)
환경: 5x5 grid world, 왼쪽 상단 start node, 오른쪽 하단 terminal node이다.
학습 시간을 고려하여 40000개의 episode에state,action,reward,next_state, dones이 저장되어있다.
dones는 해당 state가 terminal node이면 1 그렇지 않다면 0으로 저장된다.
기존 one-step td와 다르게 5개의 state,action,reward가 필요하므로 buffer가 필요하다.
state,action,reward를 buffer에 저장하고 buffer가 5개이상이 됐을 때 return을 계산후 현재 state에서 5-step 이전의 state에 업데이트 해준다.
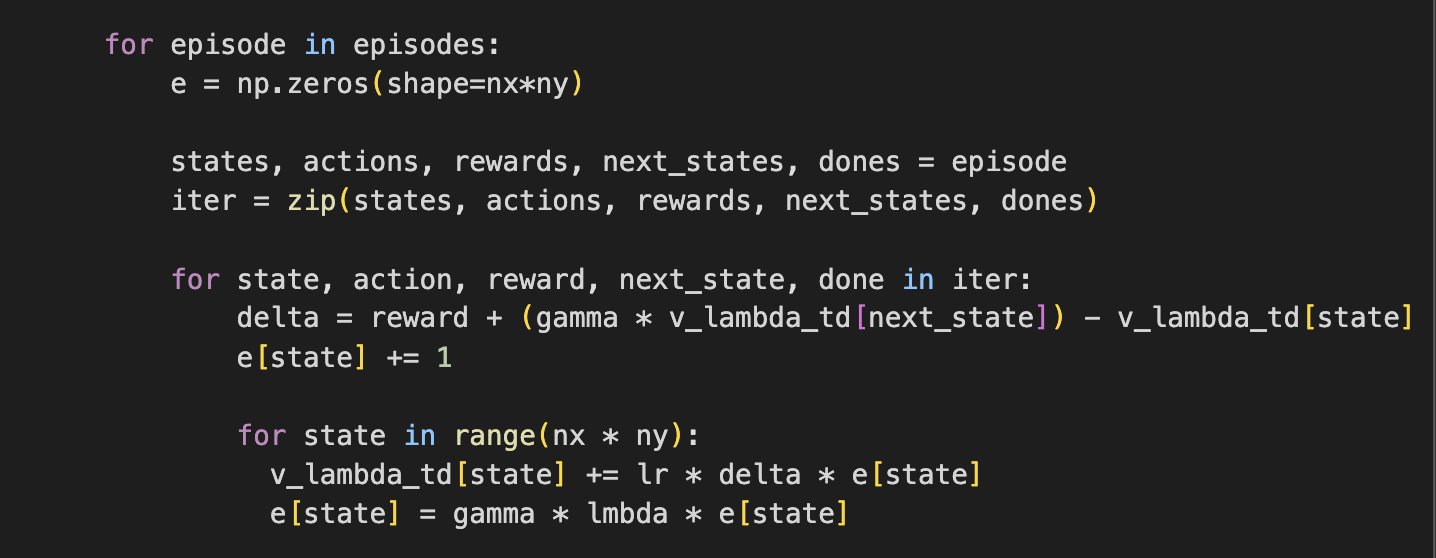
구현(backward td)
backward td는 업데이트를 역방향으로 해준다.
각 단계에서 값을 업데이트한다.
현재 state에 영향을 많이 끼친 state들에 업데이트를 해줌
->업데이트는 시간의 영향에 따라 다르게 반영함
-> 최근에 지나온 state는 높은 가중치, 오래전에 지나온 state는 낮은 가중치(Markov property를 가정하고 있기 때문에 그런거 같다)
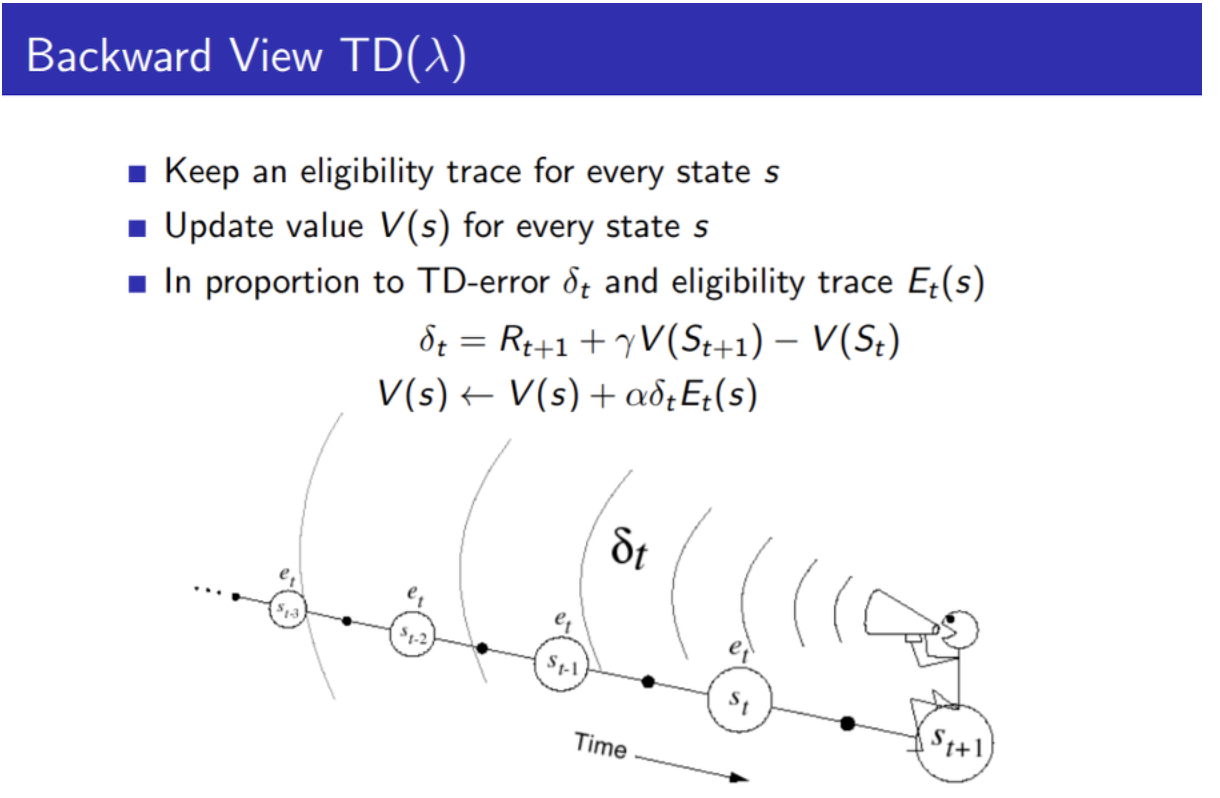
위 pseudo code를 따라 구현하였음
