1.동적 프로그래밍 = 답 재활용 하기
파이썬으로 피보나치 수열을 구해보자
가장 직관적인 방법으로는
def fibonacci(n): #재귀적 방법
if n <= 1:
return n
return fibonacci_recursive(n-1) + fibonacci_recursive(n-2)
수식 그대로 함수를 만드는 방법이 있을 것이다. 그런데 이렇게 하면 100번째 피보나치 수를 구하기 위해 호출되는 함수의 횟수는 기하급수 적으로 증가한다.(약 7해, #,###경 #,###조 ... 번 이상 함수 호출, 컴퓨터도 죽는다.)
왜냐하면, f(n-1)에서 한 번 구한 값을 f(n-2)에서 또 다시 같은 값을 구하는 과정을 반복하게 되기 때문이다.
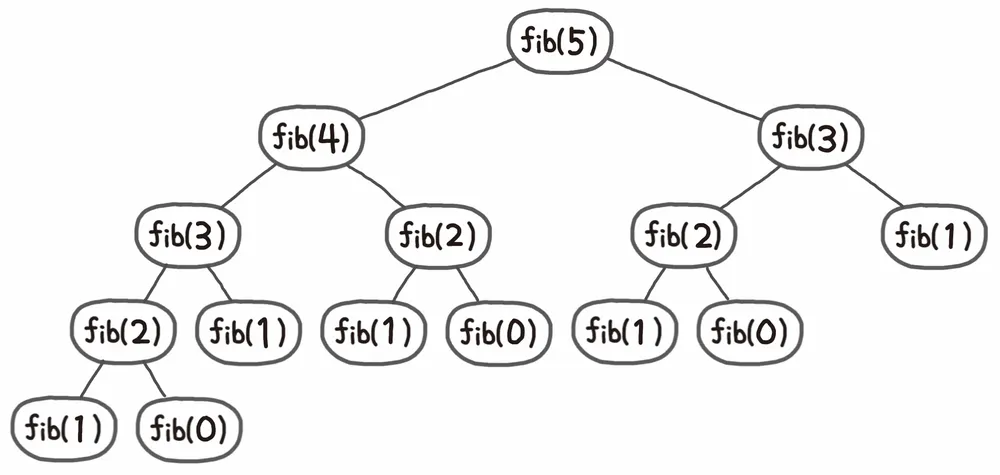
그러나 한 번 구한 작은 문제의 결과 값을 저장해두고 재사용 한다면 어떨까? 앞에서 계산된 값을 다시 반복할 필요가 없이 약 200회 내에 계산이 가능해진다.
def fibonacci(n): # 동적 프로그래밍
memo = [0] * 100
if n <= 1:
return n
if memo[n] != 0:
return memo[n]
memo[n] = fibonacci(n-1) + fibonacci(n-2)
return memo[n]이렇게 DP에서 값을 Memo에 저장해놨다가 꺼내쓰는 것을 Memoizaition이라고 한다.
2. DP 의 사용조건
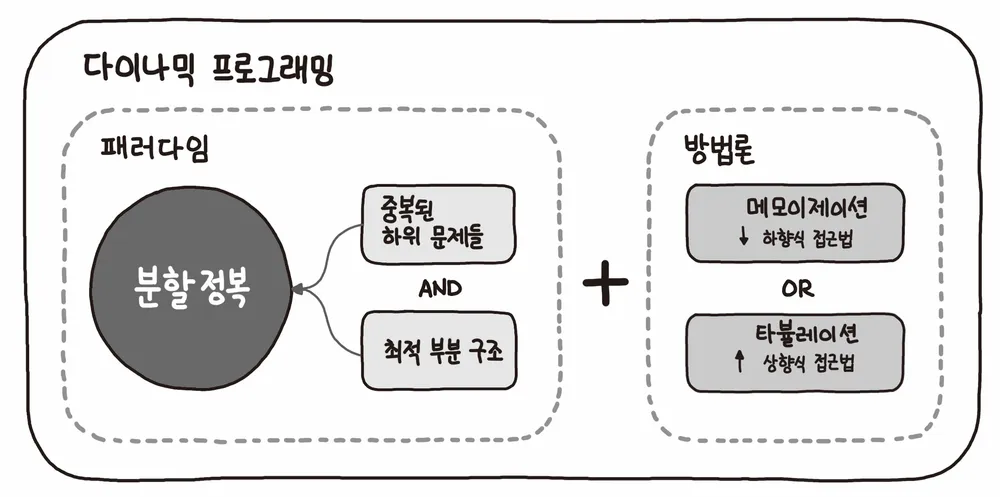
① Overlapping Subproblems
DP는 기본적으로 문제를 나누고 그 문제의 결과 값을 재활용해서 전체 답을 구한다. 그래서 동일한 작은 문제들이 반복하여 나타나는 경우에 사용이 가능하다.
즉, DP는 부분 문제의 결과를 저장하여 재 계산하지 않을 수 있어야 하는데, 해당 부분 문제가 반복적으로 나타나지 않는다면 재사용이 불가능하니 부분 문제가 중복되지 않는 경우에는 사용할 수 없다.
② Optimal Substructure(최적 부분 구조)
부분 문제의 최적 결과 값을 사용해 전체 문제의 최적 결과를 낼 수 있는 경우를 의미한다. 그래서 특정 문제의 정답은 문제의 크기에 상관없이 항상 동일하다!
만약, A - B까지의 가장 짧은 경로를 찾고자 하는 경우를 예시로 할 때, 중간에 X가 있을 때, A - X / X - B가 많은 경로 중 가장 짧은 경로라면 전체 최적 경로도 A - X - B가 정답이 된다.
3. Top-Down, Bottom-up
이름에서 알수 있듯이.. 그냥 Top-Down은 제일 큰 숫자 부터 시작해서 작은 숫자로 값을 구하는 것이고, Bottom-up은 dp[0]부터 목표 값 까지 누적시켜 답을 구하는 방식이다.
아까 본게 Top-Down 피보나치이고 , Bottom-Up 피보나치는 아래와 같이 구현한다.
def fibonacci(n): # DP Botoom-up
if n <= 1:
return n
fib = [0] * (n + 1)
fib[1] = 1
for i in range(2, n + 1):
fib[i] = fib[i - 1] + fib[i - 2]
return fib[n]참고로 Bottom-up 방식에서는 Memoization이 아니라 Tabulation이라고 한다.
다음 시간엔 대표적 DP 알고리즘인 0/1 Knapsack에 대해 다룰 예정입니다!
Reference: https://hongjw1938.tistory.com/47
