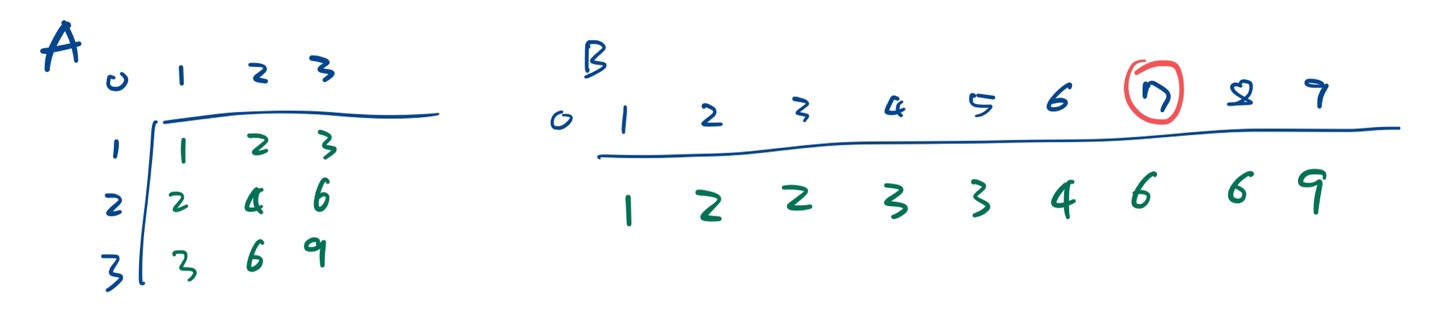이분탐색을 설명하는 글이 아니다.
이분탐색 했을때 low high mid update라는 단어들이 자연스레 떠오르지 않는 사람은 이분탐색 먼저 공부하고 와야 한다.
💍문제 파악
🙄index 1부터 쓰기
배열 A의 크기가 NxN인데 배열의 인덱스는 1부터 시작한다고 한다.
두가지중에 헷갈리기 시작한다.
배열을 A[N][N]으로 선언한다. 인덱스는 각 0 ~ N-1
배열을 A[N+1][N+1]로 선언한다. 인덱스는 각 0 ~ N
2번으로 해야 한다.
입력 N=3, k=7
출력 6
이 경우에 아래 그림과 같은 상황이 되어야 한다.
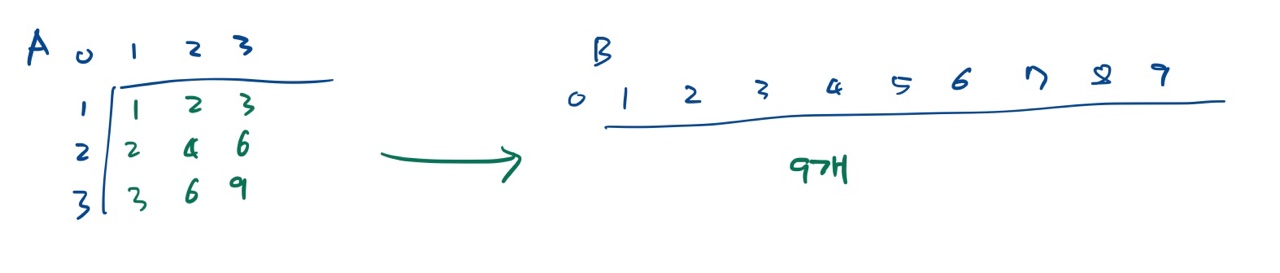
A와 B는 인덱스 1부터 시작한다.
A[3+1][3+1]로 선언하고 인덱스 1부터 이용하면 9개의 숫자를 가지게 된다.
B는 A의 숫자를 일차원 배열에 오름차순으로 저장해야 하니 B[10]이어야 한다. 인덱스 1부터 쓰면 9칸이 되도록.
그렇다면 N이 들어왔을 때 A와 B의 선언은
A[N+1][N+1]
B[N*N+1]과 같이 하면 된다.
하지만 이 문제를 풀 때 A와 B를 선언할 일은 없다.
그냥 파악만 해 두세요.
💍풀이
🙄이분탐색 (Binary Search) 이용
이 문제는 메모리 제한때문에 이분탐색을 써야 한다.
맨 밑으로 내려가면 이분탐색을 쓰지 않고 푼 코드가 있다.
초보자라면(나) 처음에 그렇게 풀었을 것이다.
어쨋든 이분탐색을 쓴 정답 코드에 대해 풀이하겠다.
🙄제출 코드
#include<iostream>
#include<algorithm>
using namespace std;
int main() {
int N, k;
cin >> N >> k;
//여기부터 이분탐색
//low high mid모두 값임
//cnt는 mid보다 같거나 작은 수의 갯수를 의미
int low = 1, high = k; //원래 N*N인데 항상 B[k]<k 라서 k로 해도 됨
while (low < high) {
int mid = (low + high) / 2, cnt = 0;
//개수 세는 부분!
for (int i = 1; i <= N; i++) {
cnt += min(N, mid / i);
}
//
if (cnt < k) low = mid + 1;
else high = mid;
}
cout << high << '\n';
}
low<high인 조건의 while문 안에서 이분탐색이 진행된다.
cnt와 k의 값을 비교해서 범위를 업데이트해간다.
조건에 맞지 않을 경우 탐색이 완료된 것으로 우리가 찾던 값인 high를 출력하고 return 0한다.
🙄변수 의미
변수 의미:
low, high, mid: 값(초록색)
cnt: mid보다 작거나 같은 값(초록)의 개수 -> 인덱스의 의미가 됨. 후술
k: 찾을 인덱스
🙄범위 업데이트 방식
이분탐색은 기준에 따라 low나 high를 mid로 업데이트해가면서 범위를 반씩 줄여간다.
이분탐색에서 가장 중요한 것이 그 기준을 뭘로 할 것인가인데 여기서는 if(cnt<k)가 범위 업데이트 기준이다.
if else문에서 업데이트하는 방식을 보면
cnt < k : cnt(mid보다 작거나 같은 값의 수)가 목표 인덱스보다 작을 때 mid를 오른쪽으로 옮긴다
cnt>= k : cnt(mid보다 작거나 같은 값의 수)가 목표 인덱스보다 클 때 mid를 왼쪽으로 옮긴다
는 뜻이 된다.

오름차순인 상태에서 인덱스는 인덱스의 해당 값보다 작거나 같은 값들의 개수라는 의미를 가진다.
결국 B[k]의 k는 B[k]보다 작거나 같은 값의 개수다.
이 업데이트 방식에선 인덱스와 값을 같이 이용한다.
출력할 값 B[k]의 범위 low, high를 지정한 뒤 비교에 이용할 기준값 mid를 지정하고 그 개수를 세어 cnt로 만든 후
cnt(mid보다 작거나 같은 값 개수)와 k(B[k]보다 작거나 같은 값 개수)를 비교한다.
같아지기까지 값의 범위를 업데이트하고 개수를 또 세면서.
위에서 low, high, mid는 값이고 cnt, k는 인덱스라고 한 게 이 말이다.
🙃cnt - 범위 업데이트 기준
cnt를 계산하는 이 코드가 가장 이해가 안될텐데 의외로 간단하다.
int low = 1, high = k; //원래 N*N인데 항상 B[k]<k 라서 k로 해도 됨
while (low < high) {
int mid = (low + high) / 2, cnt = 0;
//개수 세는 부분!
for (int i = 1; i <= N; i++) {
cnt += min(N, mid / i);
}
//
if (cnt < k) low = mid + 1;
else high = mid;
}다시 한번 cnt의미: mid(값)보다 작거나 같은 값의 개수
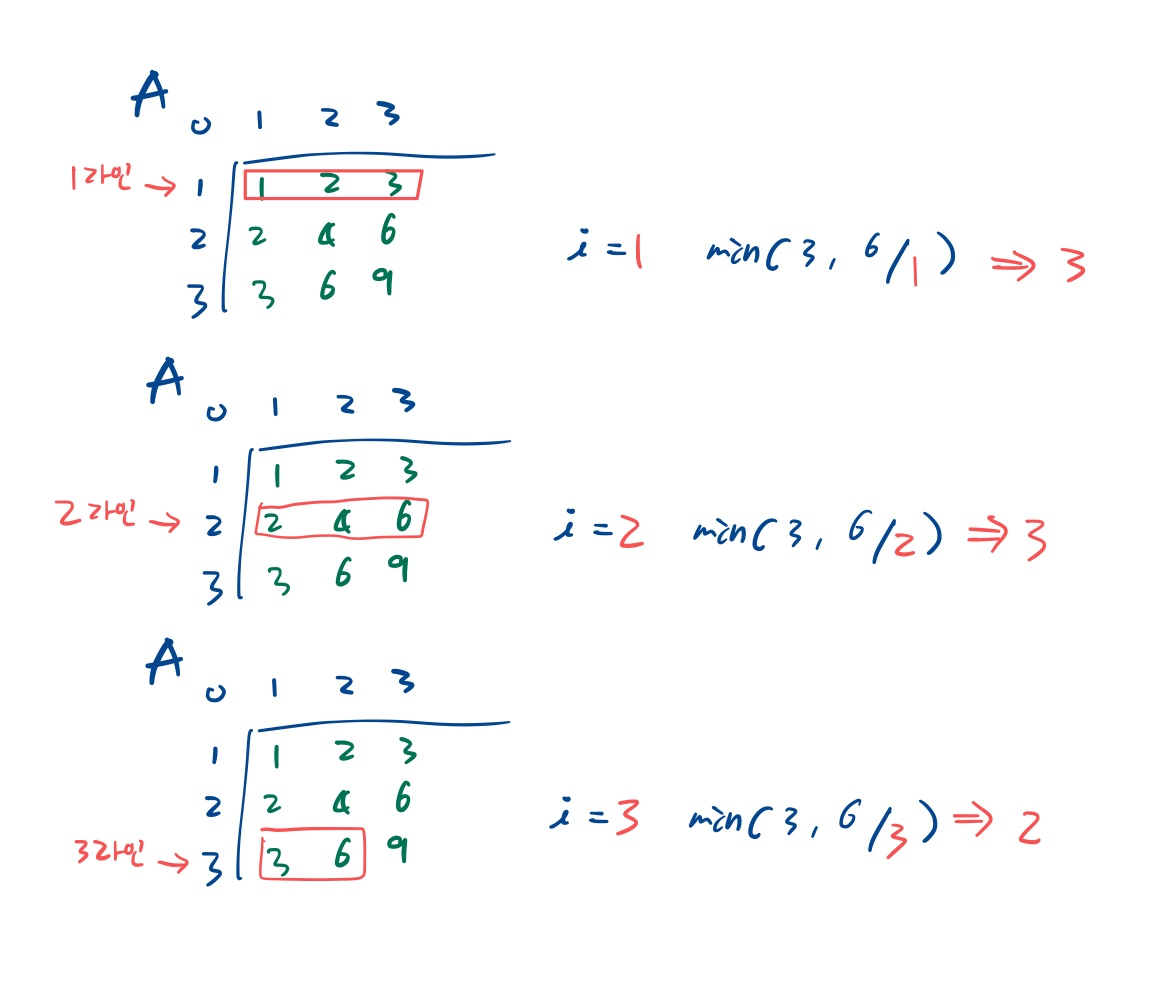
백준 입력 N=3, k=7일 때 출력은 6이다.
while문으로 들어와서 시작은 아래와 같다.
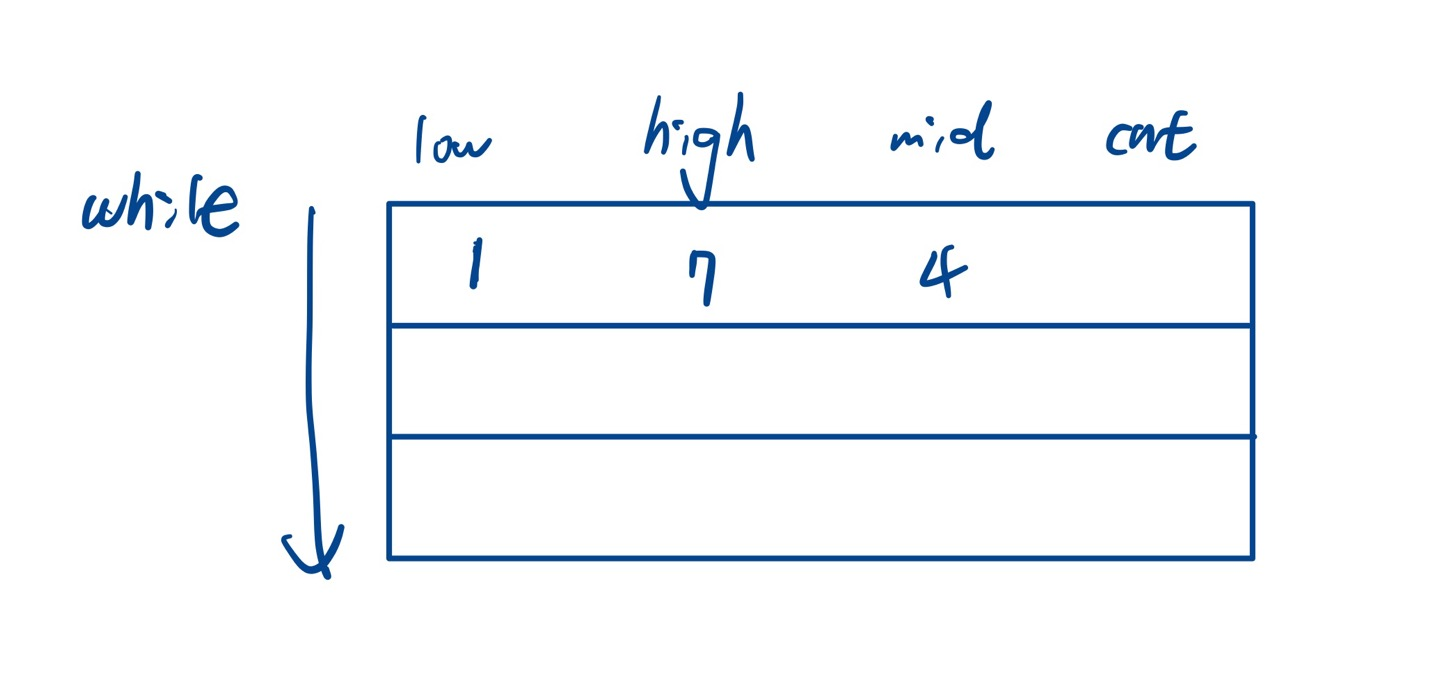
cnt는 for문 안에서 (i=0;i<N;i++){ cnt+=min(N, mid/i); } 한다.
여기서 i는 행을 의미한다. 그래서 i<N;조건으로 반복하는거고
i번째 행, 라인은 i의 배수가 최대 N개 존재한다.

먼저 i=1일 때 cnt+=min(3, 4/1)이 된다.
1의 배수 중 4보다 작은 값은 4개다. 그러나 우리가 1의 배수(1행)에서 최대 개수는 3개라서 결국 3이 된다.
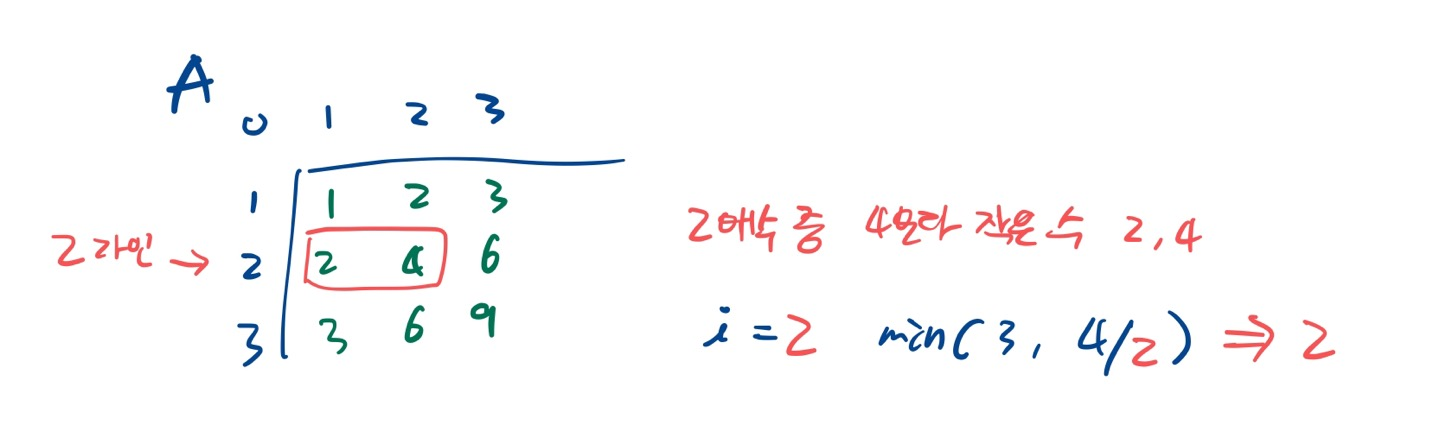
for 문을 돌아 i=2일 때 min(3, 4/2)=2이다.
2번째 행(i=2) 즉, 2의 배수 중에서 4보다 작은 수는 두개 (4/2) 다. 이것은 한 행의 숫자 개수(N=3) 보다 작으므로 그대로 2가 된다.
min(3, 2)=2와 의미가 맞는다.
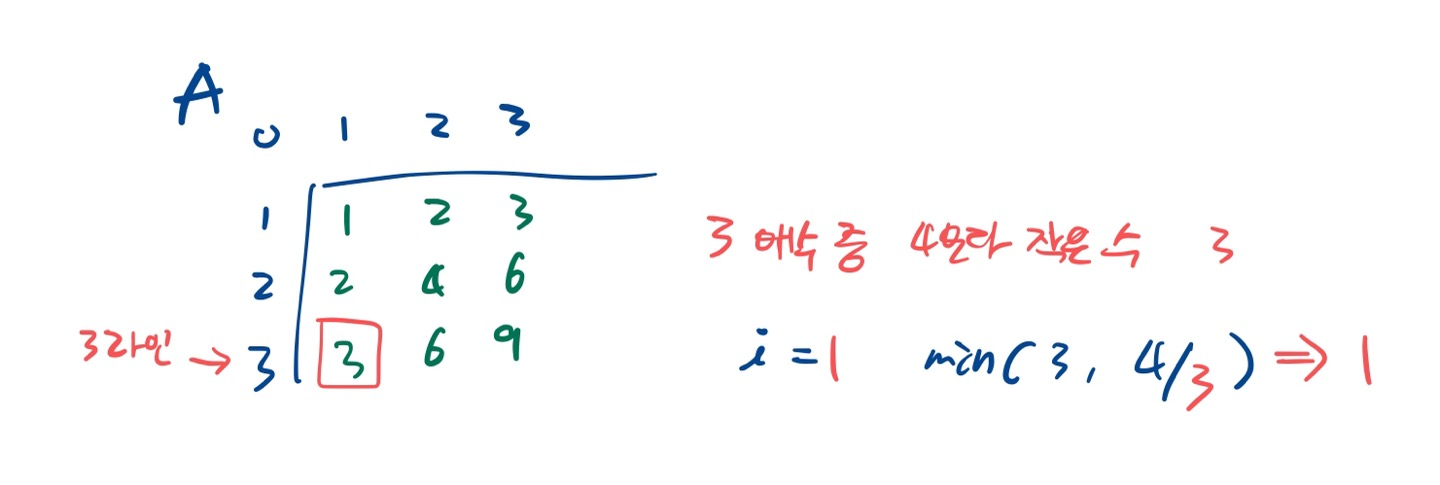
i=3일 때 min(3, 4/3)=1이다.
3의 배수중 4보다 작은 수는 4/3=1이다. 이것은 3보다 작으니 min(3, 4/3)=1이 된다.
이렇게 3개의 행을 돌며 mid=4보다 작은 값의 개수를 얻었다.
cnt=3+2+1=6이 된다.
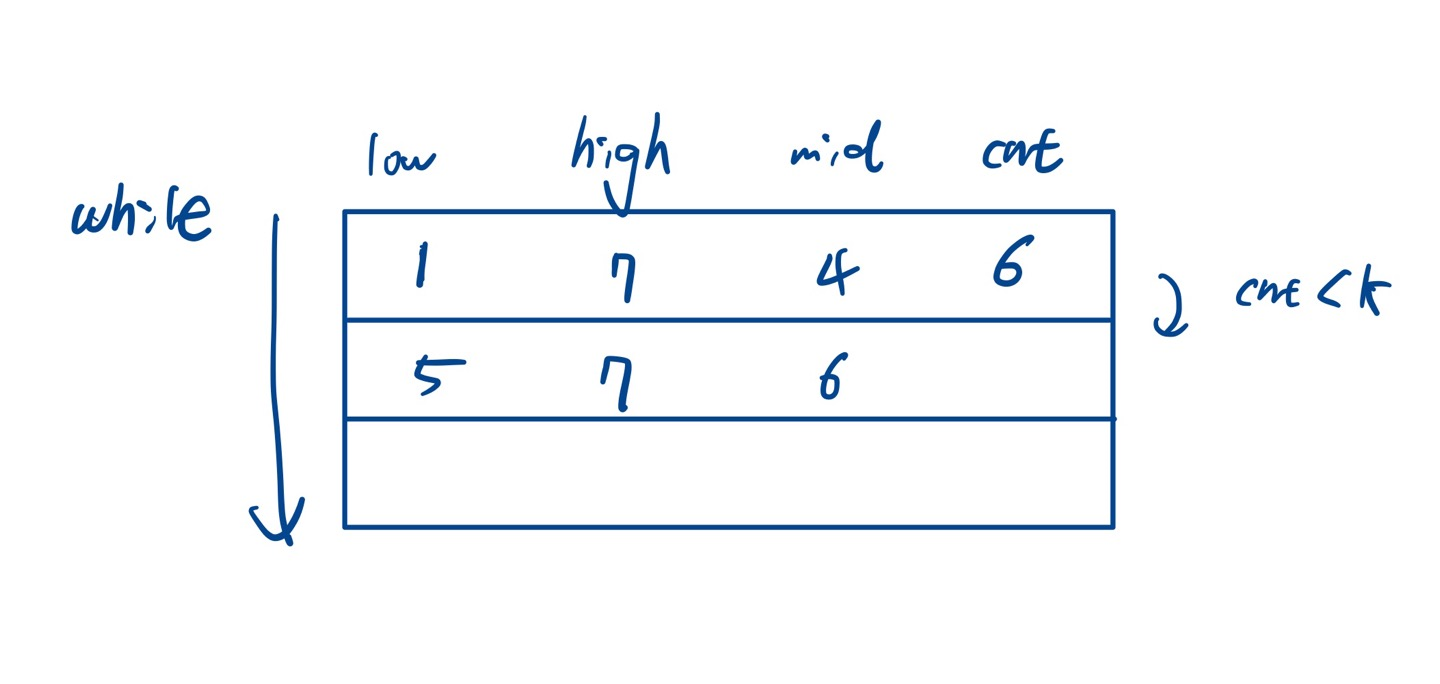
cnt가 정해졌으니 if else문에 따라 low high를 업데이트하고 다시 while문을 돈다.
똑같은 방식으로 mid보다 작거나 같은 값의 개수를 세어준다.
cnt=8
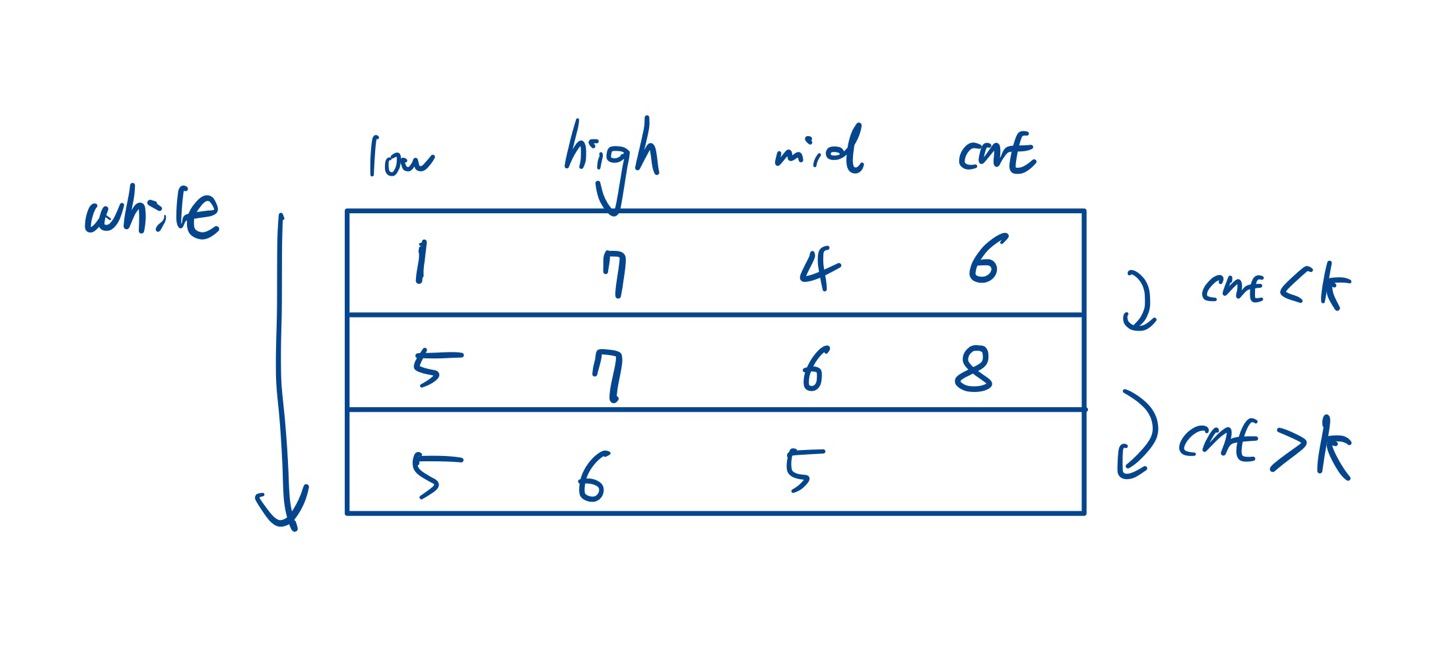
low와 high를 업데이트하고 다시 반복하면
mid보다 작은 수의 개수는 cnt=5이고 low=6으로 업데이트된다.
이후 while의 조건에 맞지 않아 그대로 high가 출력되는데 이것이 6이다.
그럼 정답이군!
🙃cnt 계산 다른 방법
이것도 cnt의 한 방법!
//개수 세는 부분!
int i;
for (i = 1; i * i <= mid; i++) {
cnt += min(N, mid / i);
}
cnt = cnt * 2 - (i - 1) * (i - 1);
//백준에서 다른 사람 풀이를 보면 거의 이 방식을 썼고 내 코드의 //개수 세는 부분!//을 위 코드로 바꿔도 문제 없이 동작한다.
왜 저런 식이 나왔는지 생각해봤는데 아직 답을 못찾았다.
아는 사람 있으면 아무나 댓글 부탁드려요.
💍이분탐색 없이 풀기
직관적이지만 1300번에서는 메모리 제한때문에 쓸 수 없다.
단순한 풀이 (이분탐색X 답은 맞지만 메모리 초과)
처음에 이렇게 풀었다 안풀린 사람이 많을것 같다 나도 그랬고.
문제 파악용으로 한번 봐도 될듯하다.
#include <iostream>
#include <algorithm> //sort
using namespace std;
int main(void) {
int N;
cin >> N;
int* B = new int[N * N + 1];
int b_idx = 1;
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
B[b_idx++] = i * j;
}
}
sort(B, B + N * N + 1); //B를 오름차순 정렬
int k;
cin >> k;
cout << B[k];
return 0;
}
1300번은 문제만 놓고 보면 아주 단순하다.
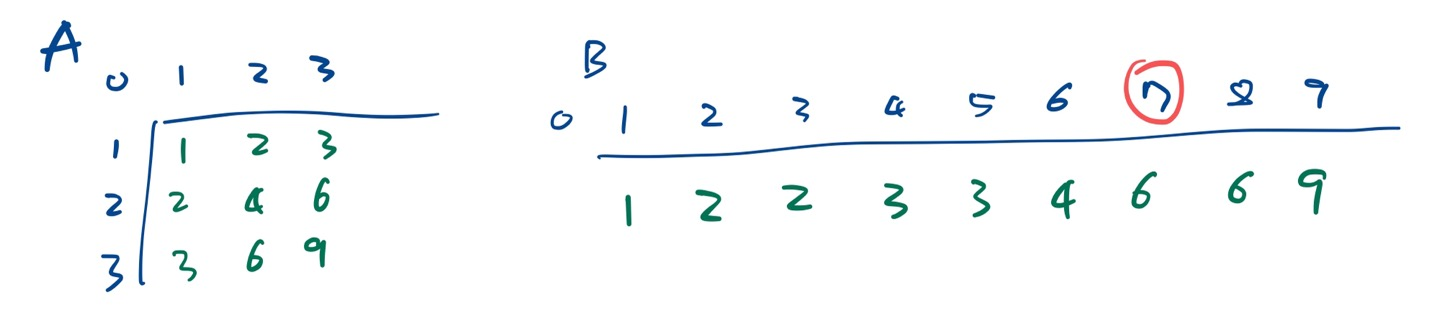
위 그림에서 보인 것처럼 A안에 들어갈 숫자들을 결국 B에 넣으면 되니
처음부터 A는 만들 필요가 없다.
이중 for문 안에서 원래 A의 원소로 들어가야 하는 i*j를 B에 바로 넣어버린다.
그 후 sort하고 B[k]를 출력하면 끝.
인데 이건 정답이 아니다.
이렇게 내보면 메모리 초과 뜸. 128MB 제한으로 꽤 빡세다.
나름 골드문제라 머리를 더 써야한다.