서칭 알고리즘 중 꼭 알아야 하는 DFS와 BFS
DFS는 Depth First Search, 깊이 우선 탐색
BFS는 Breadth First Search, 너비 우선 탐색을 말한다.
DFS와 BFS를 아예 처음 접한다면 쉽게 설명한 다른 블로그를 보는 것을 추천한다.
여기서는 간단하게만 설명한다.
자료구조에서 배우는 그래프의 개념을 모르는 사람은 그래프를 먼저 학습하길 바란다.
💍DFS와 BFS의 차이
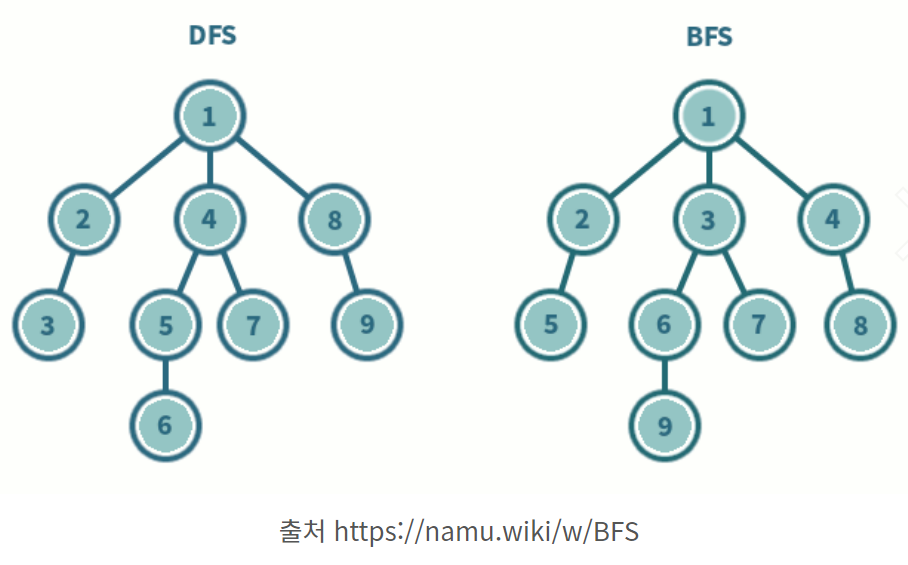
이 그림을 보면 둘의 개념이 잘 이해된다.
둘다 시작 정점이 맨 위인 상황에서
숫자는 각 알고리즘으로 탐색했을 때의 방문 순서를 나타낸다.
🙄DFS - 재귀
DFS는 간선으로 연결된 정점 중 가장 왼쪽으로 내려가고 또 그 정점에서 연결된 가장 왼쪽 정점으로 내려간다.
물론 이전에 방문하지 않았던 정점으로만 간다. 더이상 갈 곳이 없다면 다시 위로 올라와 같은 일을 반복한다.
이렇게 동작하는 방식이 마치 재귀함수를 연상시킨다. 방문한 적 없는 연결된 정점이 있으면 자기 자신의 함수를 호출하고
아닌 경우 return 하고 호출한 지점으로 다시 돌아간다. 이 말이 이해되지 않는다면 재귀함수를 먼저 공부하고 오는 것이 좋다.
🙄BFS - queue
연결된 정점을 쭉 타고 들어갔던 DFS와 달리 BFS는 이웃한 것을 먼저 모두 방문한다.
현재 정점 1에 연결된 이웃 정점2,3,4을 모두 방문하고 그 다음엔 2,3,4에 대해 순서대로 그에 이웃한 정점을 모두 방문한다.
이것은 queue를 이용해 구현할 수 있다.
🙄연결된 정점 중 선택하는 기준
위에서 DFS, BFS 모두 연결된 정점 중 왼쪽에 있는 정점부터 방문하는 것을 알 수 있다.
구현할 때 유의할 점이다. 후술한다.
💍코드
#include <iostream>
#include <vector>
#include <algorithm> //sort 들어있음
#include <queue>
#include <string.h> //memset 들어있음
using namespace std;
vector<int> vec[1002];
vector<int> result_dfs;
vector<int> result_bfs;
bool visit[1002]; //방문 여부: 정점에다가 표시
void dfs(int x) {
visit[x] = true;
result_dfs.push_back(x);
for (int i = 0; i < vec[x].size(); i++) {
if (!visit[vec[x][i]]) { //간선의 의미를 잘 보자..
dfs(vec[x][i]);
}
}
}
void bfs(int temp) {
queue<int> q;
q.push(temp);
visit[temp] = true;
while (!q.empty()) {
int x = q.front();
q.pop();
result_bfs.push_back(x);
for (int i = 0; i < vec[x].size(); i++) {
if (!visit[vec[x][i]]) {
q.push(vec[x][i]);
visit[vec[x][i]] = true;
}
}
}
}
int main(void) {
int n, m, v, a, b;
cin >> n >> m >> v;
for (int i = 1; i <= m; i++) {
cin >> a >> b;
vec[a].push_back(b);
vec[b].push_back(a); //양방향 간선처리
}
//sort해야함. 왼쪽부터 순서대로라고 생각하기 때문. 왼쪽은 작은 숫자고.
//sort안하려면 matrix쓰고 왼쪽에서 오른쪽으로 탐색해야함.
for (int i = 1; i <= n; i++) {
sort(vec[i].begin(), vec[i].end()); //벡터 안에서 sort
}
dfs(v);
for (int i = 0; i < result_dfs.size(); i++) { //정점 개수니까 n으로 for문 돌려도 되지 않을까?
//안됨. 간선이 없는 경우 정점을 모두 탐색하지 않을수도 있음
cout << result_dfs[i] << ' ';
}
cout << endl;
memset(visit, false, 1002);
bfs(v);
for (int i = 0; i < result_bfs.size(); i++) {
cout << result_bfs[i] << ' ';
}
return 0;
}🙄설명
정답으로 방문 순서를 출력해야 하니 result_dfs, result_bfs를 선언해준다.
vec[i]는 i번 노드와 연결된 정점을 저장한 vector이다.
visit[i]는 i번 정점이 방문되었는지 여부를 저장하는 bool이다.
dfs()와 bfs()는 각각 재귀와 큐를 이용했고 위의 설명을 보면 이해될 것이다.
둘 다 시작점을 받고 return 형은 void이다.
main 안의 첫 for문은 문제에서 양방향 그래프라고 했기 때문이다.
🙃sort하는 이유
그 다음에 바로 sort하는데 위에서 설명한 '왼쪽부터' 때문이다. 안해보면 일단 틀리는걸 확인할 수 있다.
예를 들어 vec[1]에 4,5,6,2가 들어있다고 하자. 1번 노드에 4,5,6,2번 노드가 연결되있다는 뜻이다.
만약 1번 노드가 탐색 시작 노드라면 DFS든 BFS든 다음 노드는 4가 될 것이다. 하지만 문제의 정답은 다음 노드가 2여야 한다.
그래서 탐색 전에 오름차순 정렬을 해줘야 한다.
이 부분은 코드를 수정해 matrix(2차원 벡터나 2차원 배열)을 이용할 경우 생략할 수 있다. 그냥 for문 돌리면 오름차순과 같으니..
🙃생각해 보자
여기서 하나 생각해볼 것은 result_bfs의 크기이다. result_bfs를 출력할 때 for문에서 그냥 정점 개수인 n을 사용하면 안될까?
안된다.
간선으로 다른 정점과 연결되지 않은 채 덩그러니 존재하는 정점이 있다면 그 정점은 탐색되지 않는다.
그러니 result_bfs의 사이즈가 정점 개수보다 작을 수 있다.
🙃함수들
sort(시작주소, 끝주소); //오름차순 정렬
memset(주소, 채울 값, 주소부터 몇 칸 채울지 정수); //memory set
코드 참고:
https://hagisilecoding.tistory.com/16
https://jun-itworld.tistory.com/18
