Java 숫자와 타입(Number & Type)

Java 숫자 데이터 타입

세상에는 다양한 데이터가 존재한다. 대표적으로 숫자와 문자가 있다. 사람의 경우 1234.567 이라는 숫자가 실수이고 '.'을 기준으로 연산을 해야한다는 것을 알고 있지만 컴퓨터는 1234.567 이라는 숫자만 보고는 이것이 정수인지 실수인지 심지어는 문자인지 알 수 없다.
이런 문제를 해결하기 위해 우리는 어떤 데이터를 컴퓨터가 연산하기 전, 컴퓨터에게 미리 정해놓은 타입중 어떤 타입인지를 알려주고 그에 따라 데이터를 연산할 수 있게 한다.

자바에서는 숫자 데이터를 크게 정수 타입과 실수 타입으로 나눈다. 정수 타입과 실수 타입안에서 크기별로 타입들에 더 세부적으로 나누는데 이는 컴퓨터의 성능 한계(메모리 한계)로 인해 메모리를 효율적으로 사용하기 위함이다. 만약 10이라는 정수를 계속해서 변경없이 저장할 예정인데 10억을 저장할 수 있는 메모리에 저장해놓는다면 메모리를 낭비하고 있는 것이니 말이다.

1. 정수 타입(Integer Types)

정수 타입은 다음과 같이 4가지로 구성된다.

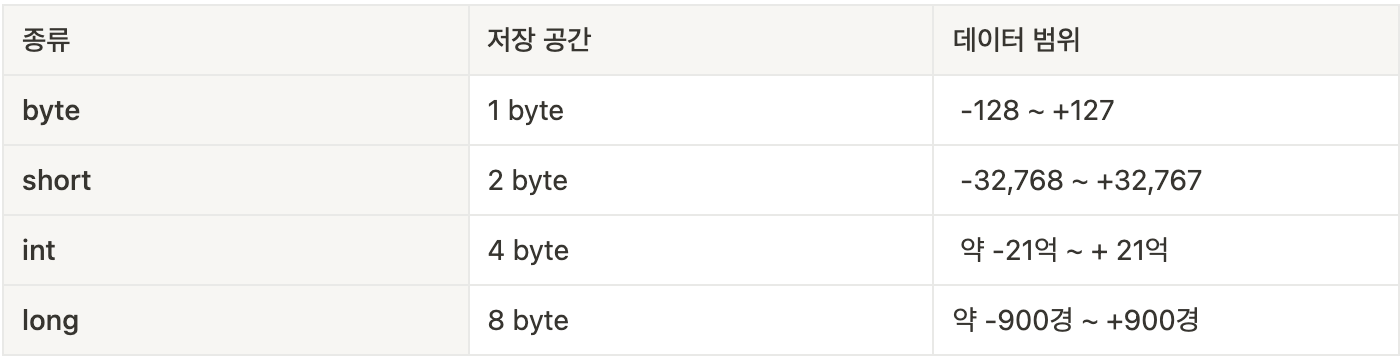
int 범위를 넘어가는 long 값

만약 long 변수에 2200,000,000과 같이 int의 데이터 범위 초과하는 값을 대입하려면 L 접미사를 을 붙여줘야 한다.(소문자 l도 되지만 실제로 써보면 1과 매우 헷갈려 대문자 L을 사용하는게 좋아보인다.)
Java는 수를 변수에 저장하기 전 먼저 메모리에 저장하게 되는데 이때, 메모리에 저장하는 형태가 기본으로 int형이기에 long형이 저장된다고 알려주기 위함이다.

long moreThanInt = 2200000000	// x
long moreThanInt = 2200000000L	// o

underscore 표기법

JDK 7부터 underscore 표기법을 지원한다. 위와 같이 크기가 큰 정수의 경우 한눈에 파악하기 어려운 점이 있어 실생활에서 2200,000,000와 같이 표기하듯 1000단위로 밑줄 문자를 표시하여 큰 정수를 한눈에 파악할 수 있게 지원한다.

long moreThanInt = 1000000000
long moreThanIntUnderScore = 1000_000_000	// underscore 표기

2진수 / 8진수 / 16진수

기본적인 정수 자료형은 10진수를 기준으로 표현된다. 하지만 컴퓨터는 0,1만이 존재하는 2진수로 모든 데이터를 읽게되고 이에 발맞추어 2진수, 8진수, 16진수 또한 개발자가 표현할 수 있도록 지원한다.

int oct = 023;		// 0(숫자 '0')으로 시작하면 8진수
int hex = 0xC;		// 0x(숫자 '0' + 알파벳 'x')로 시작하면 16진수   
int bin = 0b101;	// 0b(숫자 '0' + 알파벳 'b')로 시작하면 2진수   

2. 실수 타입(Floating-Point Types)

자바의 실수를 표현하기 위한 자료형은 대표적으로 float, double 이 있다.
과거에는 실수를 표현할 때 float형을 많이 사용했지만, 하드웨어의 발달로 인한 메모리 공간의 증가로 현재에는 double형을 가장 많이 사용한다.

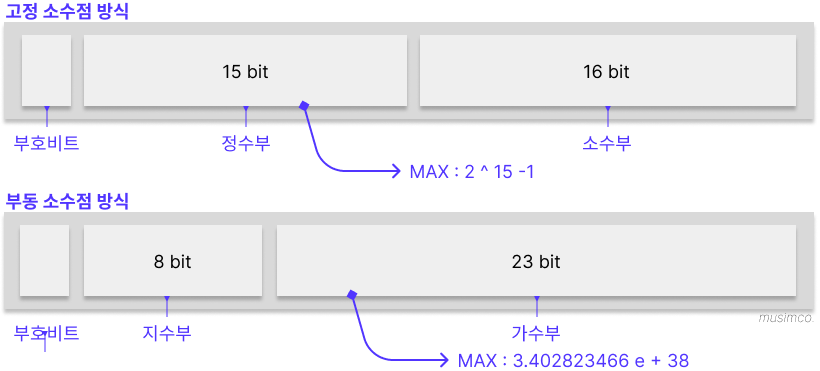
부동 소수점 방식

정수를 표현할 수 있는 범위에 제한이 있듯 실수의 소숫점을 표현할 수 있는 범위에도 제한이 존재한다. 실수의 부정확한 연산의 한계를 최소화하기 위해 컴퓨터에서는 소수를 이진법으로 표현할때 고정 소수점 방식이 아닌 부동 소수점 방식을 사용한다.
부동 소수점 방식은 소수를 있는 그대로 나타내는 방식이 아닌 가수부와 지수부로 나누어 저장하는 방식으로 사용하면 매우 큰 범위의 실수까지도 표현할 수 있어 보다 정밀하게 소수를 표현할 수 있다.

고정 소수점 방식에서는 따로 물리적으로 정수부와 소수부로 나누어 각각 15bit, 16bit 밖에 사용하지 못하지만 부동소수점 방식은 실수의 값 자체를 가수부(23bit)에 넣어 표현하기 때문에 보다 큰 비트의 범위를 가지게 되며, 정수부가 크든 소수부가 크든 상관없이 가수부 내에서 전체 실수를 표현하기 때문에 공간 낭비 문제도 해결된다.

그러나 이러한 부동 소수점 방식에는 크리티컬한 문제가 존재하는데..

소수 계산 오차

0.625 같이 이진수 소수점으로 딱 떨어지는 수는 문제없지만 0.1 와 같이 부동 소수점 방식으로 변화하여 저장하면 0.0001100110011... 로 무한 반복되는 이진수 실수는 아무리 큰 수를 저장하는 부동 소수점 방식이라 해도 무한대를 저장할수 없다. 결국 메모리 한계까지 소수점을 집어넣고 어느 부분에서 끊어 반올림을 해주어야 한다. 이와 같이 반올림된 값을 이용하여 계산한다면 오차가 발생할 수 있다. 다음의 예시를 살펴보자.

double value1 = 34.1;
double value2 = 66.1;

System.out.println(value1+value2);
// output : 100.19999999999999

value1 과 value2를 계산한 결과로 100.2가 나와야 하지만 100.19999999999999 같은 부정확한 계산 결과가 나왔다.

이와 같은 문제를 해결하기 위해 다음과 같은 방법을 생각해볼 수 있다.

해결 방법 1 . 정수형으로 만들어 계산

double value1 = 34.1;
double value2 = 66.1;

double result = (value1 * 100 + value2 * 100) / 100;
System.out.println(result);

위 방식은 실수들에 10^n을 곱해 정수로로 만든 후 계산 후 실수로 만드는 방식이다. 9자리를 넘지 않으면 int 자료형을, 18자리를 넘지 않으면 long 자료형을 사용하면 된다. 근데 만약 소수의 자리수가 18자리를 넘는다면? 어떻게 하면 좋을까? (예를 들어 3.14159265358979323846 같은 경우...)

만일 소수의 크기가 18자리를 초과하면 BigDecimal 클래스를 사용해야 한다.

해결 방법 2 . BigDecimal 클래스

BigDecimal bigDecimalVal1 = new BigDecimal("34.1");
BigDecimal bigDecimalVal2 = new BigDecimal("66.1");

BigDecimal addResult = bigDecimalVal1.add(bigDecimalVal2);
System.out.println(addResult);

BigDecimal 클래스를 사용할 경우 기본형 타입보다 실행 속도가 느려진다는 단점이 있지만 거대한 수의 정확한 계산을 도와주는 좋은 클래스이니 실수 계산시 항상 손에 들고 있으면 좋을 것 같다.

그렇다고 모든 부분을 다 믿을 순 없어

부동 소수점 방식으로 표현된 소수들은 가수부에만 실제 유효한 수를 저장할 수 있다. 즉 가수부에서 표현할 수 있는 부분을 벗어난 부분은 신뢰할 수 없는 부분이고 해당 범위는 가수부의 크기를 파악하면 확인할 수 있다.

신뢰할 수 있는 부분의 범위 : log10(2^가수부 크기)

다음 공식을 사용하여 계산하면
float의 경우 가수부의 크기가 23 bit로 log10(2^23) = 7.224
double의 경우 가수부의 크기가 52 bit로 log10(2^52) = 15.653
즉, float은 소수점 7번째 자리 정도, double은 소수점 15번째 자리 정도까지 신뢰할 수 있다는 사실을 알 수 있다.

데이터 타입 형변환

Java에서 연산은 "2(byte 데이터 타입) + 3(byte 데이터 타입)" 과 같이 동일한 데이터 타입에서 가능하다. 하지만, 프로그램을 만들다 보면 "2(byte 데이터 타입) + 3.5(double 데이터 타입)"과 같이 서로 다른 데이터 타입간의 연산이 필요할 때가 있다.

이럴경우 변수의 데이터 타입을 바꿔주는 작업이 필요한데, 이것이 데이터 타입의 형변환(타입변환)이다. 이러한 형변환(타입변환)에는 크게 자동 형변환(Promotion) 과 강제 형변환(Casting) 이 있다.

감당할 수 있다면 | 자동 형변환(Promotion)

자동 형변환(Promotion)은 프로그램 실행 도중에 자동적으로 형변환(타입변환)이 일어나는 것을 말한다. 이런 자동 형변환은 '감당할 수 있다면' 일어난다. 다음 코드를 봐보자.

byte a = 10; // 정수 10을 byte 데이터 타입의 변수인 a에 저장
int b = a;   // byte 데이터 타입의 변수인 a를 int 데이터 타입의 변수인 b에 저장

다음과 같이 작은 메모리 크기의 데이터 타입(byte a)에서 큰 메모리 크기의 데이터 타입(int b)에 값을 저장하면, 별다른 문법 없이 프로그램 실행 도중 자동으로 타입변환이 일어난다.

다음은 자동 형변환이 일어나는 순서이다.

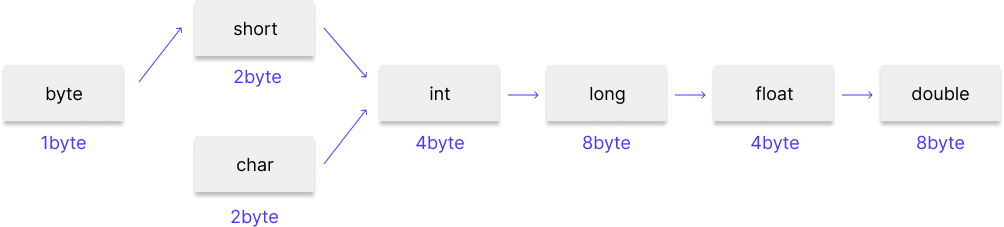
위 그림에서 순서를 살펴보면 byte의 모든 값은 short로, short의 값은 int로, int의 값은 long으로 표현할 수 있어 자동적으로 형변환이 되는 것을 확인할 수 있다.

그런데 long -> float 부분은 long의 경우 8byte고 float은 4byte니까 float에서 long으로 자동 형변환이 되야하지 않을까? 라고 생각할 수 있다.

이는 long과 float 각각이 표현할 수 있는 범위를 생각해보면 된다.
long의 경우 9,223,372,036,854,775,807(19자리)까지 표현하고
float의 경우 3.4X10^38(38자리)까지 표현한다.

즉, float으로 표현할 수 있는 범위가 long보다 더 크고 이는 float이 long을 감당할 수 있다는 뜻이므로 long이 차지하는 메모리는 더 크지만 long에서 float으로 자동 형변환이 일어난다.

강제로 맞춰주기 | 강제 형변환(Casting)

앞서 살펴본 자동 형변환이 일어나는 순서를 거슬러 형변환을 시도한다면 에러가 발생한다.

int intVal = 1;
byte byteVal = intVal; // error

그런데 생각해보면 위와 같이 intVal에 1을 저장하는 경우 이를 byteVal도 충분히 저장할 수 있다. 이와 같이 해당 값이 형변환 방향을 거스르더라도 충분히 값을 유지하고 저장할 수 있다고 생각되는 경우 강제 형변환을 진행할 수 있다.

int intVal = 1;
byte byteVal = (byte)intVal;

만약 강제 형변환시 형변환하는 수가 변화하는 타입이 표현할 수 있는 수보다 크다면 다음과 같이 잘못된 수가 저장되게 된다.

int intVal = 128;	// byte는 127(2^7-1)을 최대로 표현할 수 있다.
byte byteVal = (byte)intVal;

System.out.println("byteVal = " + byteVal);	// byteVal = -128

연산에서의 형변환

+, -, *, / 과 같은 기본적인 사칙연산은 같은 타입의 피연산자 간에만 수행되기 때문에 서로 다른 데이터 타입의 피연산자가 있을 경우 두 피연산자 중 크기가 큰 타입으로 자동 형변환(Promotion)된 후 연산이 수행된다.

int intVal = 100;
long longVal = 8000;

long resultLong = intVal + longVal;
System.out.println("resultLong = " + resultLong);

만약 int 데이터 타입의 연산 결과를 얻고 싶다면, 강제 형변환(Casting)을 사용하면 된다.

int intVal = 100;
long longVal = 8000;

int resultInt = intVal + (int)longVal;
System.out.println("resultInt = " + resultInt);

공부 자료

[JAVA] ☕ 타입 형변환 원리 & 방법 💯 총정리 _ Inpa Dev
03-01 숫자 (Number) _ WikiDocs