[알고리즘] 병합정렬이란

합병 정렬(merge sort) 알고리즘의 개념 요약

• ‘존 폰 노이만(John von Neumann)’이라는 사람이 제안한 방법

• 일반적인 방법으로 구현했을 때 이 정렬은 안정 정렬 에 속하며, 분할 정복 알고리즘의 하나 이다.

  • 분할 정복(divide and conquer) 방법
    • 문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략이다.
    • 분할 정복 방법은 대개 순환 호출을 이용하여 구현한다.

• 과정 설명

  1. 리스트의 길이가 0 또는 1이면 이미 정렬된 것으로 본다. 그렇지 않은 경우에는
  2. 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
  3. 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
  4. 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.

합병 정렬(merge sort) 알고리즘의 구체적인 개념

• 하나의 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법이다.

• 합병 정렬은 다음의 단계들로 이루어진다.

  • 분할(Divide): 입력 배열을 같은 크기의 2개의 부분 배열로 분할한다.
  • 정복(Conquer): 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출 을 이용하여 다시 분할 정복 방법을 적용한다.
  • 결합(Combine): 정렬된 부분 배열들을 하나의 배열에 합병한다.

• 합병 정렬의 과정

  • 추가적인 리스트가 필요하다.
  • 각 부분 배열을 정렬할 때도 합병 정렬을 순환적으로 호출하여 적용한다.
  • 합병 정렬에서 실제로 정렬이 이루어지는 시점은 2개의 리스트를 합병(merge)하는 단계 이다.

  

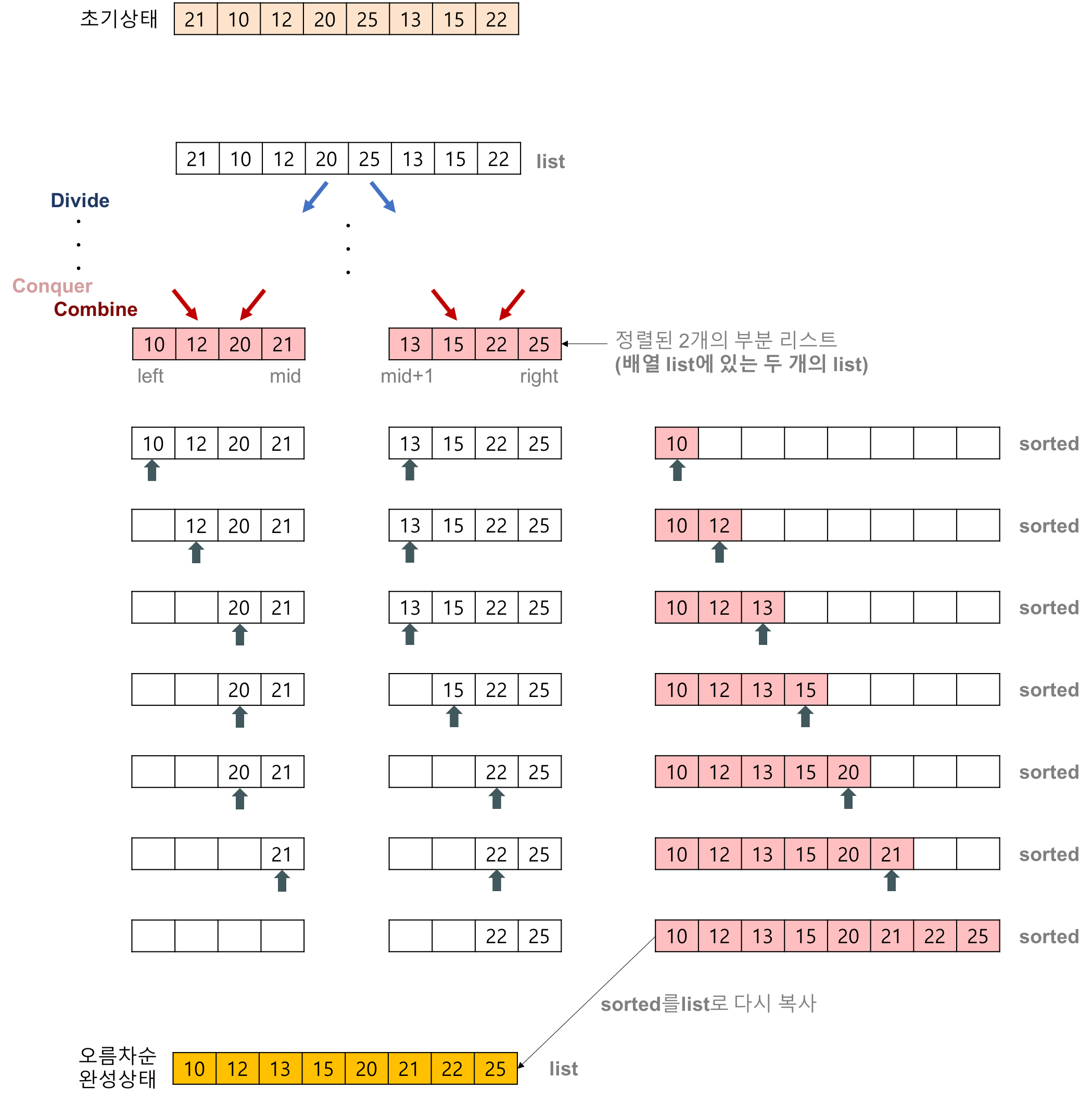
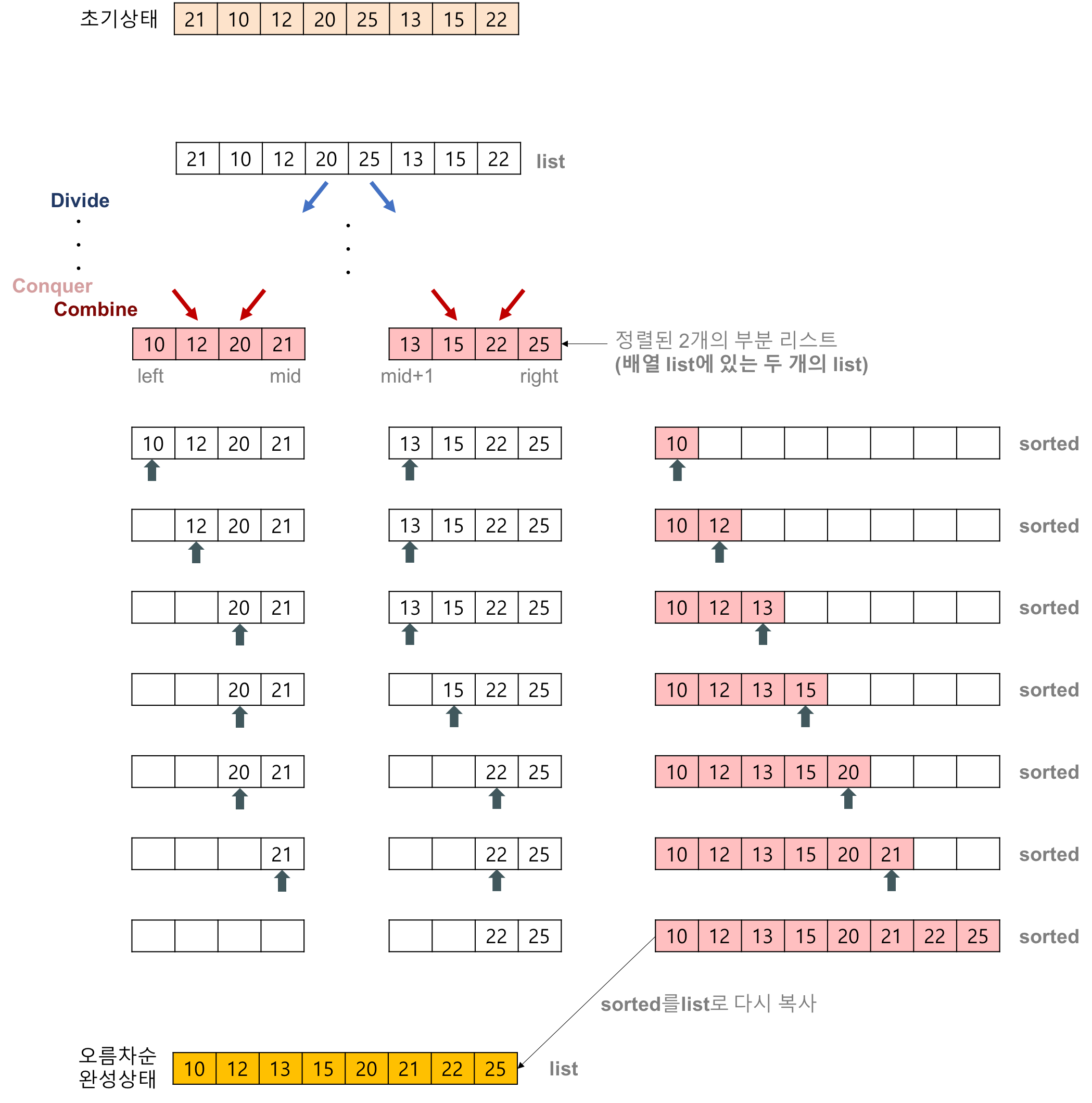
합병 정렬(merge sort) 알고리즘의 예제

• 배열에 27, 10, 12, 20, 25, 13, 15, 22이 저장되어 있다고 가정하고 자료를 오름차순으로 정렬해 보자.
• 2개의 정렬된 리스트를 합병(merge)하는 과정

1. 2개의 리스트의 값들을 처음부터 하나씩 비교하여 두 개의 리스트의 값 중에서 더 작은 값을 새로운 리스트(sorted)로 옮긴다.
2. 둘 중에서 하나가 끝날 때까지 이 과정을 되풀이한다.
3. 만약 둘 중에서 하나의 리스트가 먼저 끝나게 되면 나머지 리스트의 값들을 전부 새로운 리스트(sorted)로 복사한다.
4. 새로운 리스트(sorted)를 원래의 리스트(list)로 옮긴다.

합병 정렬 구현

private void solve() {
    int[] array = { 230, 10, 60, 550, 40, 220, 20 };
 
    mergeSort(array, 0, array.length - 1);
 
    for (int v : array) {
        System.out.println(v);
    }
}
 
public static void mergeSort(int[] array, int left, int right) {
    if (left < right) {
        int mid = (left + right) / 2;
 
        mergeSort(array, left, mid);
        mergeSort(array, mid + 1, right);
        merge(array, left, mid, right);
    }
}
 
public static void merge(int[] array, int left, int mid, int right) {
    int[] L = Arrays.copyOfRange(array, left, mid + 1);
    int[] R = Arrays.copyOfRange(array, mid + 1, right + 1);
 
    int i = 0, j = 0, k = left;
    int ll = L.length, rl = R.length;
 
    while (i < ll && j < rl) {
        if (L[i] <= R[j]) {
            array[k] = L[i++];
        } else {
            array[k] = R[j++];
        }
        k++;
    }
 
    while (i < ll) {
        array[k++] = L[i++];
    }
 
    while (j < rl) {
        array[k++] = R[j++];
    }
}

퀵소트와의 차이점

퀵정렬 : 우선 피벗을 통해 정렬(partition) → 영역을 쪼갬(quickSort)

합병정렬 : 영역을 쪼갤 수 있을 만큼 쪼갬(mergeSort) → 정렬(merge)

합병 정렬(merge sort) 알고리즘의 특징

• 장점
  • 안정적인 정렬 방법
    • 데이터의 분포에 영향을 덜 받는다. 즉, 입력 데이터가 무엇이든 간에 정렬되는 시간은 동일하다. (O(nlogn)로 동일)
  • 만약 레코드를 연결 리스트(Linked List)로 구성하면, 링크 인덱스만 변경되므로 데이터의 이동은 무시할 수 있을 정도로 작아진다.
    • 제자리 정렬(in-place sorting)로 구현할 수 있다.
  • 따라서 크기가 큰 레코드를 정렬할 경우에 연결 리스트를 사용한다면, 합병 정렬은 퀵 정렬을 포함한 다른 어떤 졍렬 방법보다 효율적이다.
• 단점
  • 만약 레코드를 배열(Array)로 구성하면, 임시 배열이 필요하다.
    • 제자리 정렬(in-place sorting)이 아니다.
  • 레코드들의 크기가 큰 경우에는 이동 횟수가 많으므로 매우 큰 시간적 낭비를 초래한다.

시간복잡도

평균	최선	최악
Θ(nlogn)	Ω(nlogn)	O(nlogn)

참고

https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
https://github.com/gyoogle/tech-interview-for-developer/blob/master/Algorithm/MergeSort.md