그래프
개념들 간의 관계도를 도식화해서 나타낸 자료구조이다.
그래프 탐색의 목적은 모든 정점을 한 번씩 방문하는 것이다. (=완전탐색)
그래프 실생활 예
- 지도, 내비게이션
- SNS / 메신저
- VSC (Version Control System) 버전 관리 시스템
그래프 구성
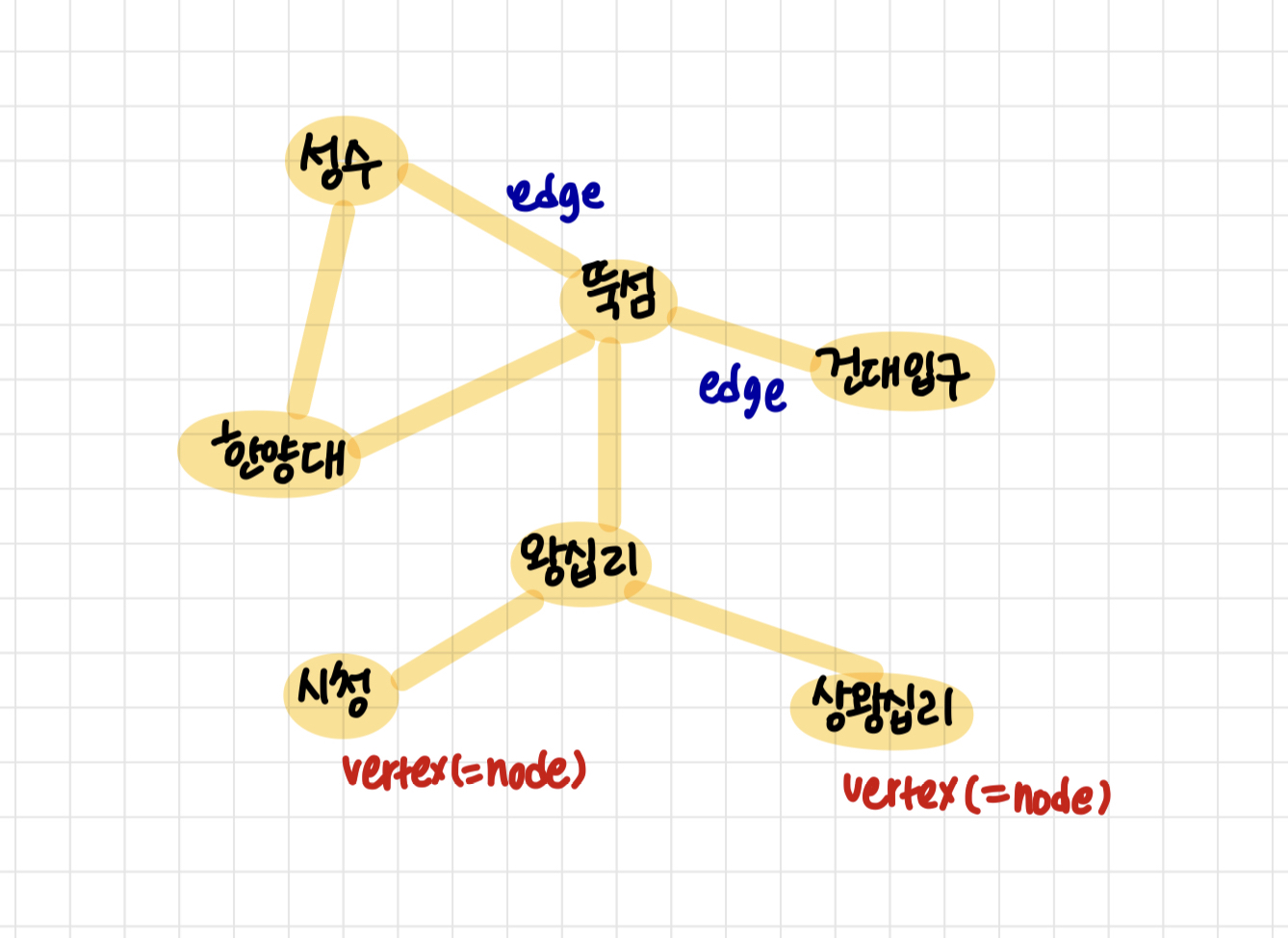
그래프는 정점(vertex)와 간선(edge)로 이루어져있다.
그래프 탐색 문제는 대부분 정점의 개수와 간선의 개수가 주어진다.
그래프 종류
- 방향성
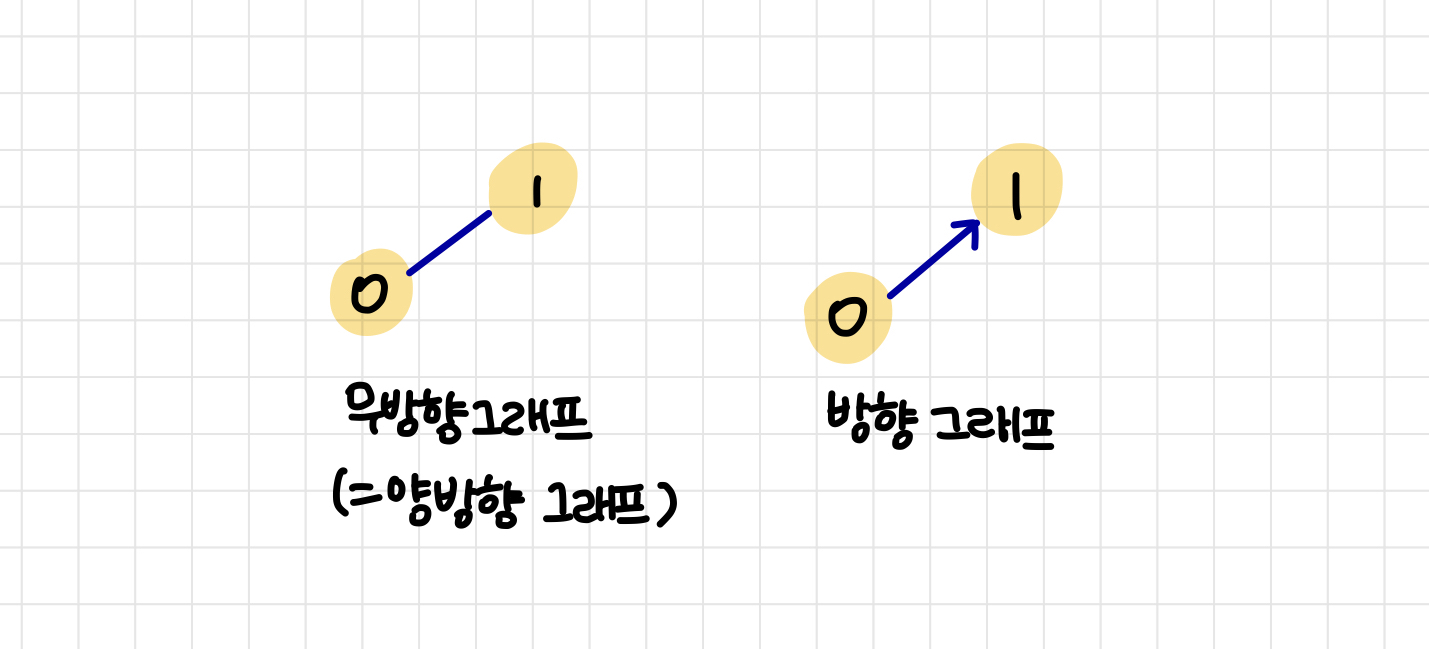
그래프는 방향이 없는 무방향 그래프와 방향성이 있는 방향 그래프로 나뉜다.
무방향 그래프는 방향성이 없으므로 양방향 그래프와 같다.
- 순환성
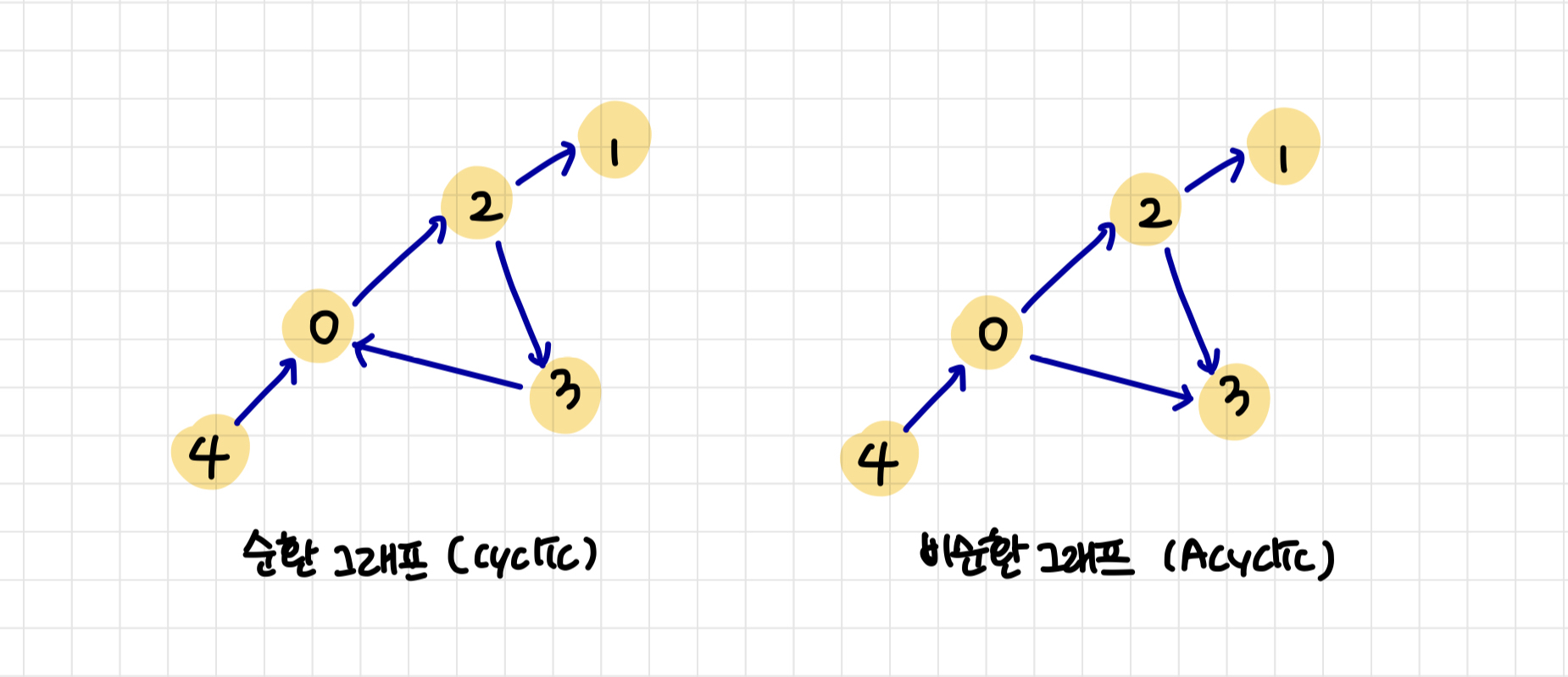
순환그래프는 무한히 돌 수 있는 사이클이 있는 그래프를 말한다.
비순환 그래프는 어느 한 군데도 사이클이 없는 그래프이다.
특히 이 중에서 방향성이 존재하는 비순환 그래프는 DAG(Directed Acyclic Graph) 라고 부른다.
DAG는 과거에서 미래로 방향성을 가지며, 과거로 되돌아 갈 수 없기 때문에 사이클이 존재하지 않는다.
대표적인 DAG의 예시로는 VSC(Version Control System)이 있다.
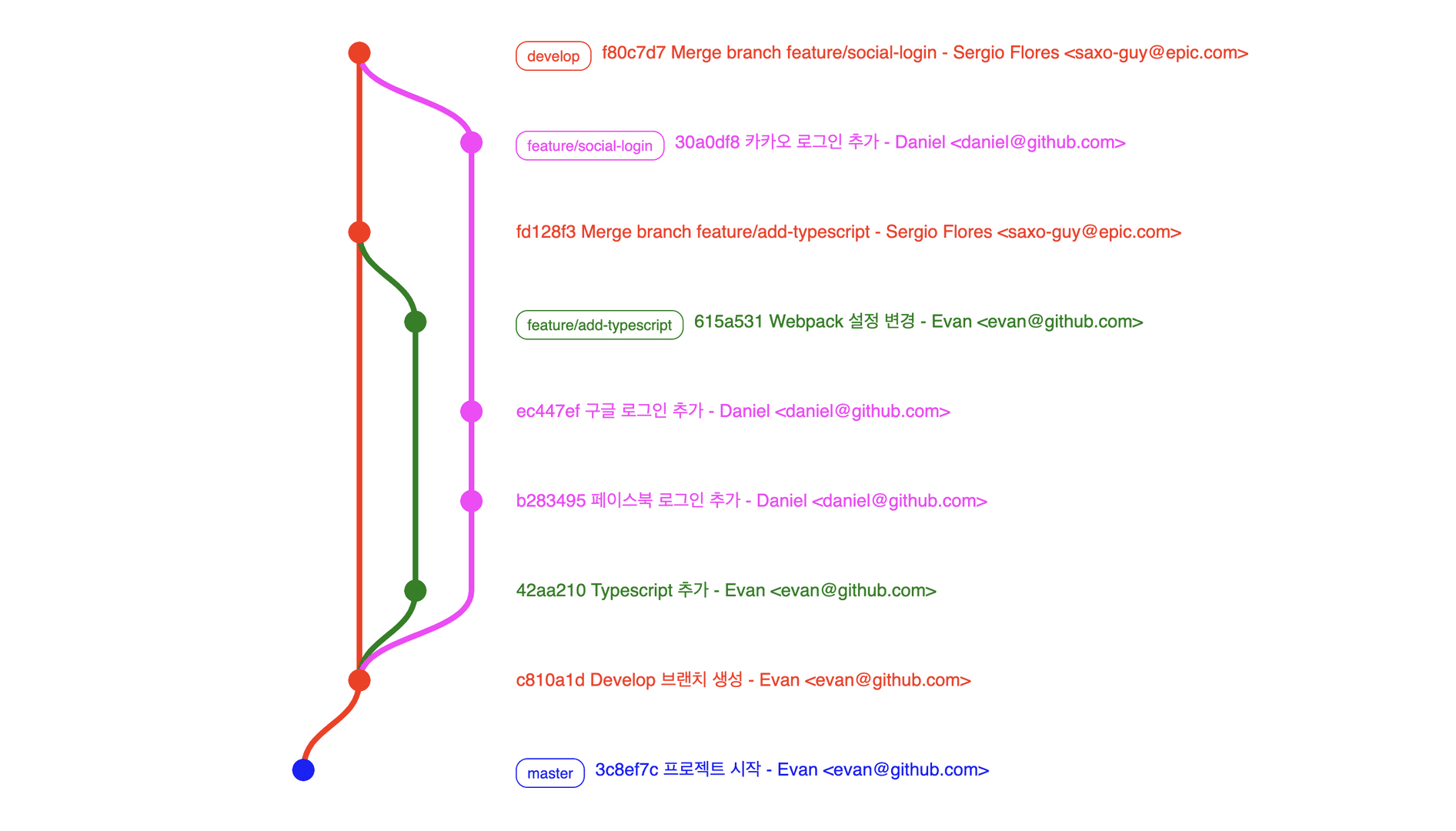
(깃의 버전 관리시스템)
연결요소
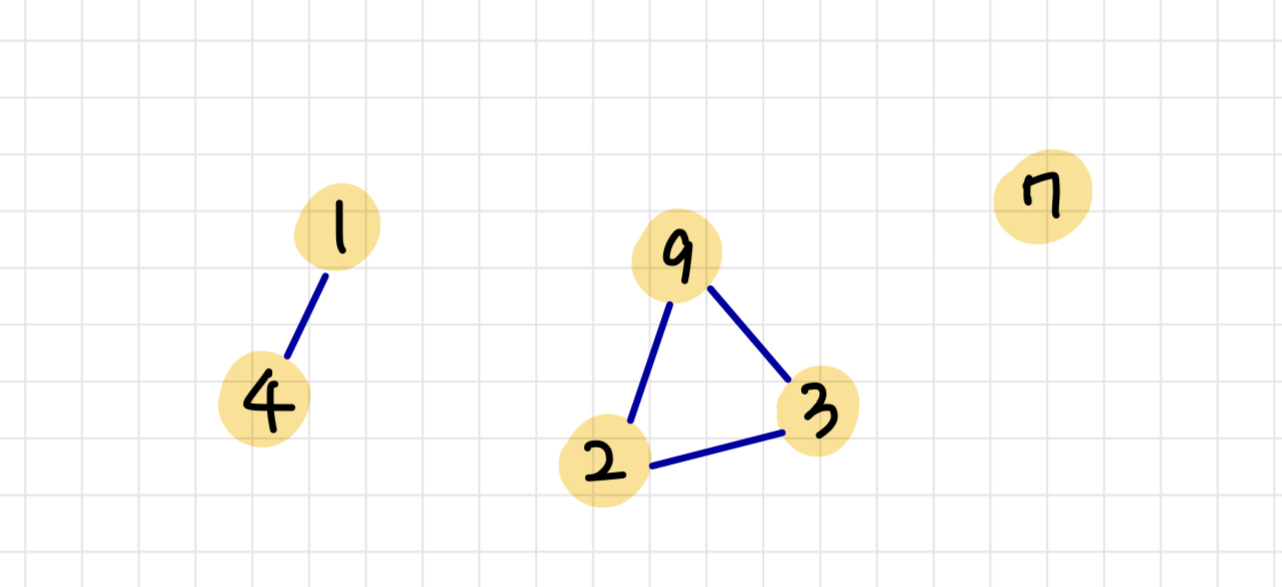
위의 그림은 정점이 6개 간선이 4개인 그래프이다.
각각은 연결요소이다. 연결되어 있는 정점의 개수로 연결 요소의 개수를 파악한다.
위의 7과 같이 간선이 없는 정점의 경우도 연결 요소 1개라고 표현할 수 있다.
위의 연결요소는 {1, 4}, {9, 2, 3}, {7} 로 총 3개이다.
그래프를 코드로 나타내기
그래프는 인접 행렬 형태와 인접 리스트 형태로 나타낼 수 있다.
[ 인접 행렬 ]
만약 그래프의 가로, 세로의 크기가 N이고 N=4 인 문제가 주어졌다고 가정하자.
우선, 4*4 그래프를 그리고 모두 0으로 초기화한다.
그 후 방향, 무방향 그래프에 따라 그래프가 다르게 그려진다.
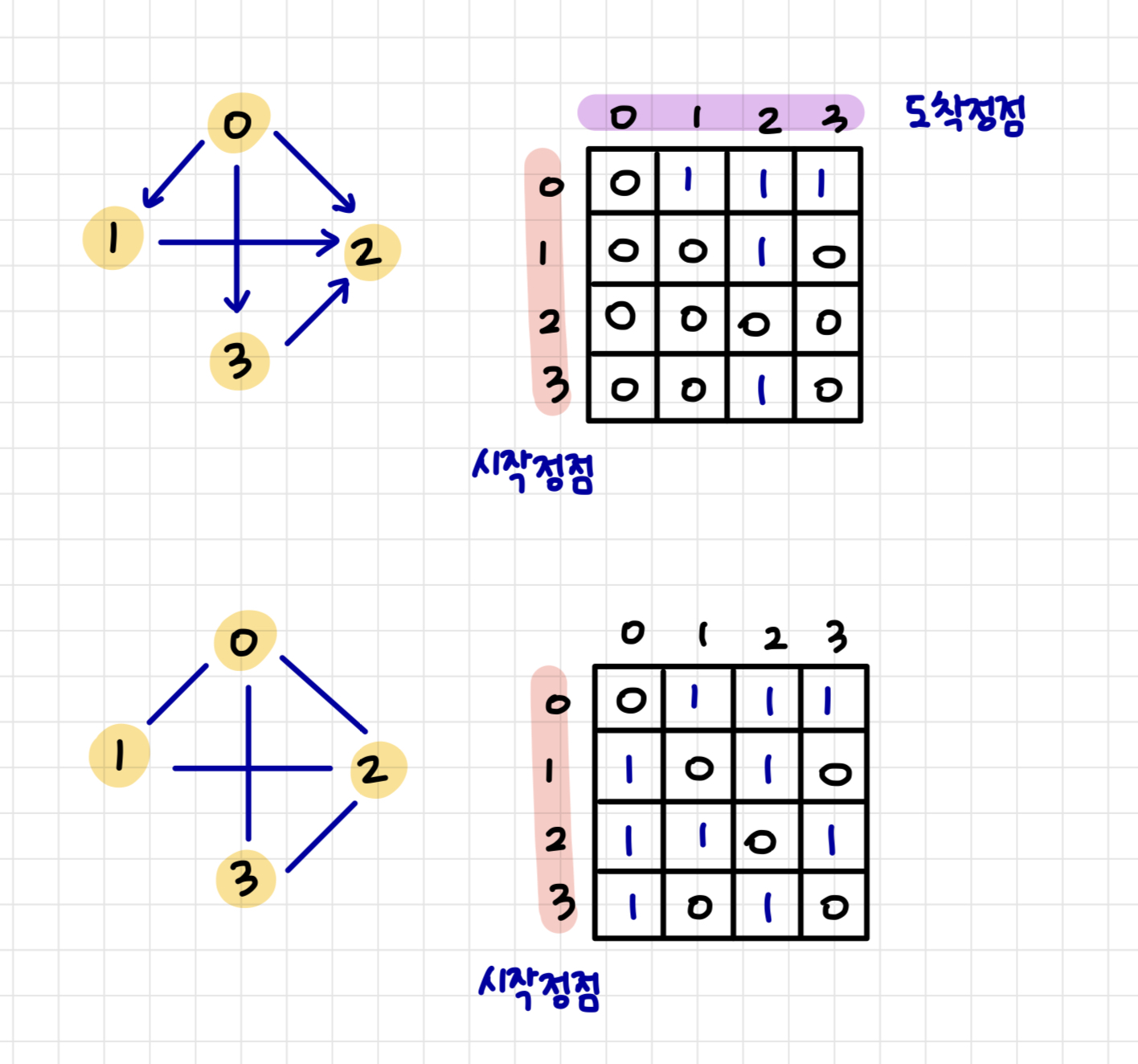
방향 그래프의 경우 행의 인덱스를 시작 정점으로, 열의 인덱스를 도착 정점으로 생각하면 이해하기 수월하다.
무방향 그래프의 경우도 마찬가지 이지만, 방향이 없기 때문에 해당 정점과 인접한 모든 정점에 1을 표시한다.
인접 행렬의 경우 간선의 개수와 상관없이 노드가 N개이면 무조건 N^2 만큼 메모리를 사용한다.
- 시간 복잡도: O(V^2)
코드로 나타내면 다음과 같다.
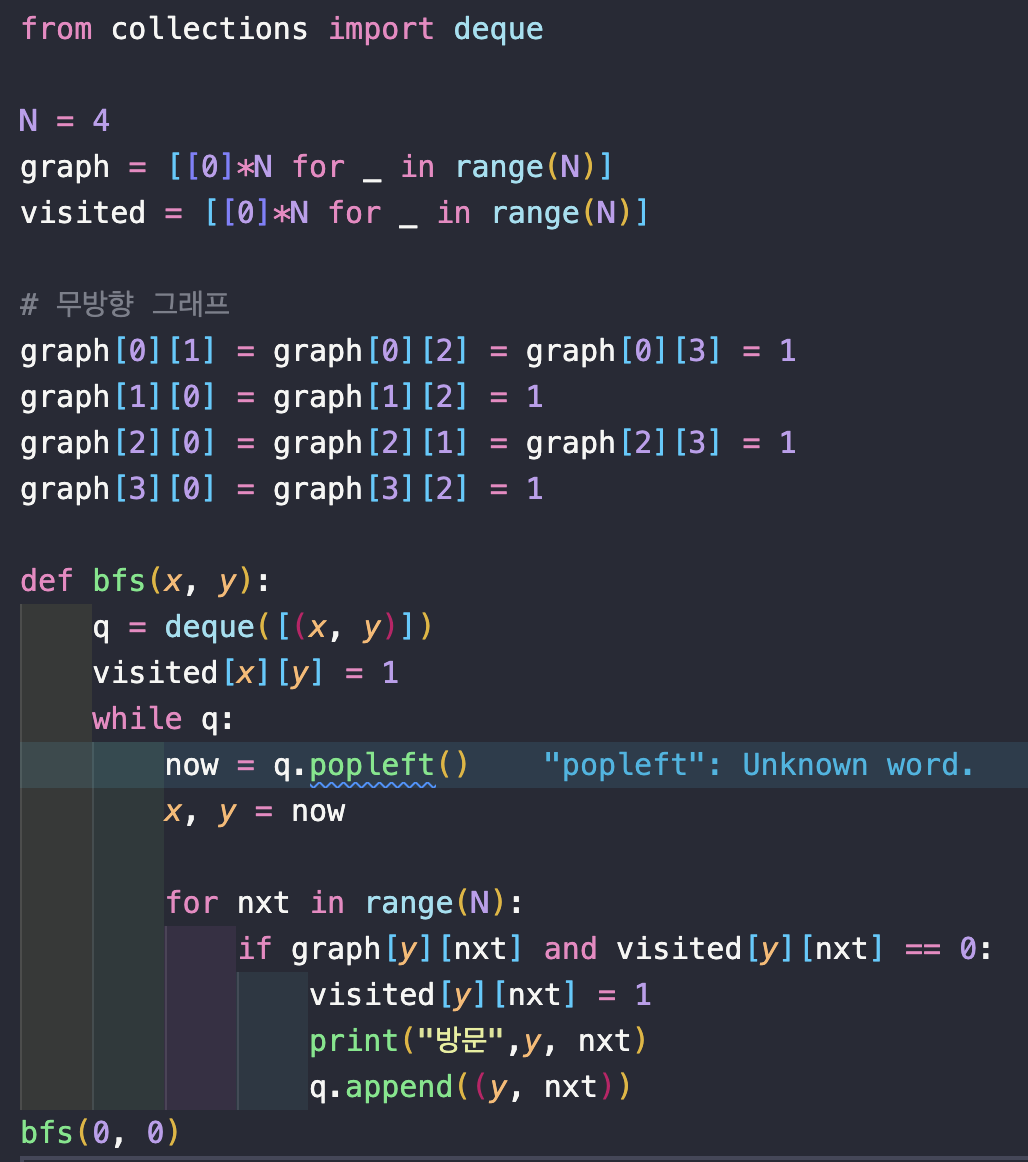
[ 인접 리스트 ]
같은 그래프를 인접 리스트 형식으로 저장할 수도 있다.
방향 그래프의 경우 각 정점이 가르키는 노드를 연결리스트 형태로 표현하고, 무방향 그래프의 경우 각 정점과 인접해있는 노드를 연결리스트 형태로 표현한다.
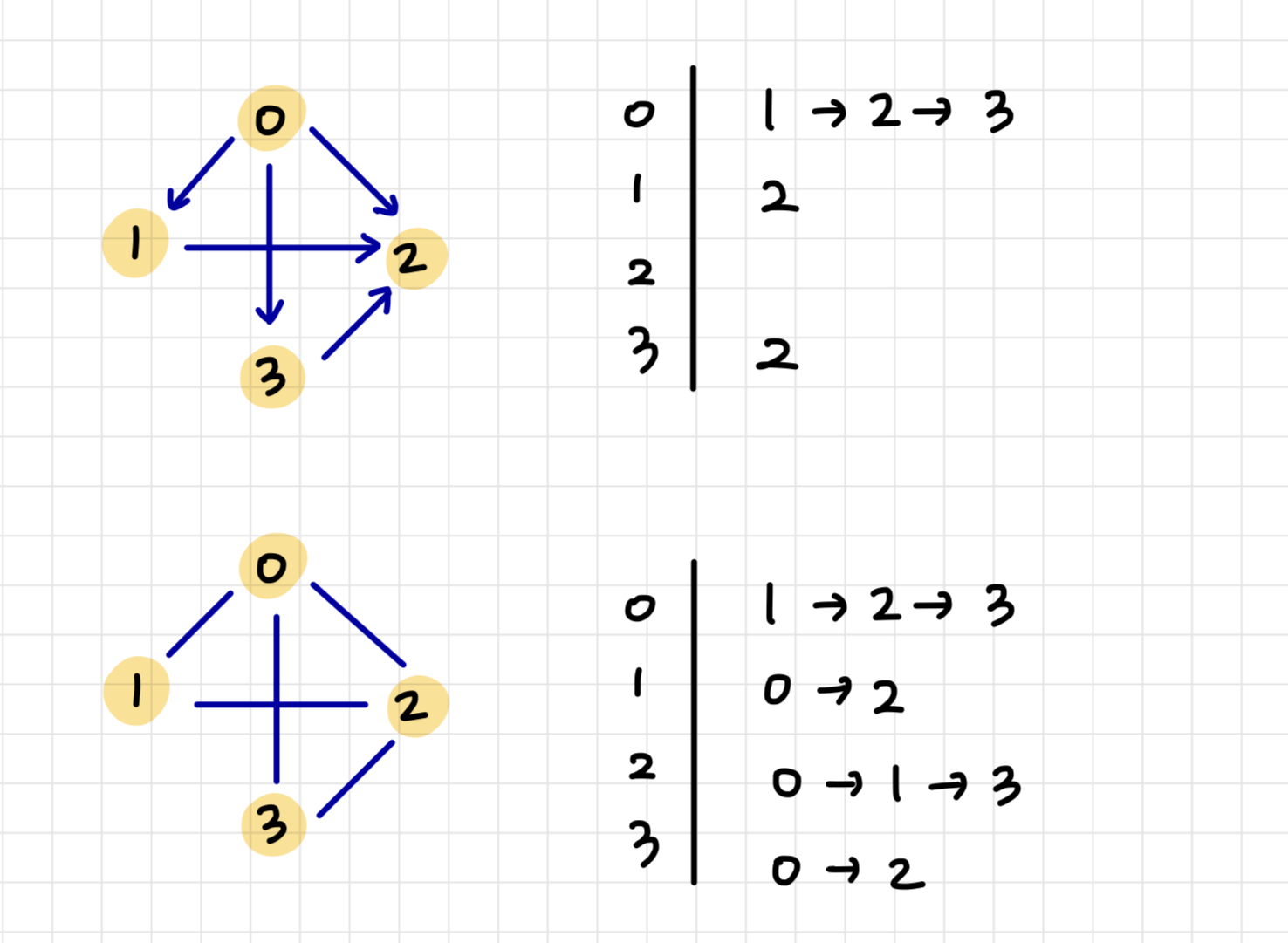
마찬가지로 그래프 요소의 인덱스를 시작 정점으로, 해당 인덱스에 있는 리스트를 도착 정점으로 생각하면 이해가 수월하다.
- 시간 복잡도: O(V+E)
코드로 나타내면 다음과 같다.
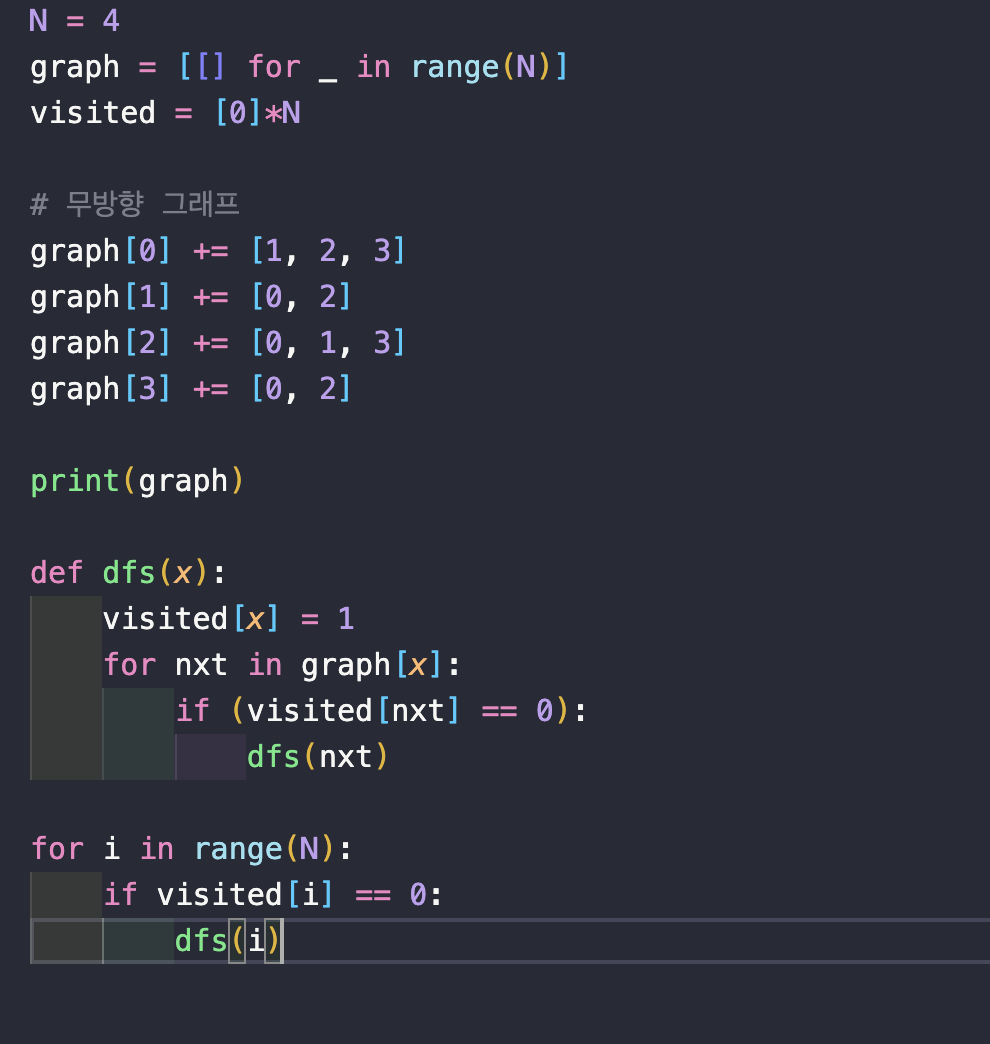
이와 같이 그래프 탐색에는 대표적인 두 가지 알고리즘인 BFS, DFS가 있다.
자세한 내용은 다음 포스트에서 다루겠다!
