[백준] 2583번: 영역 구하기 - c++

영역 구하기

문제

입력

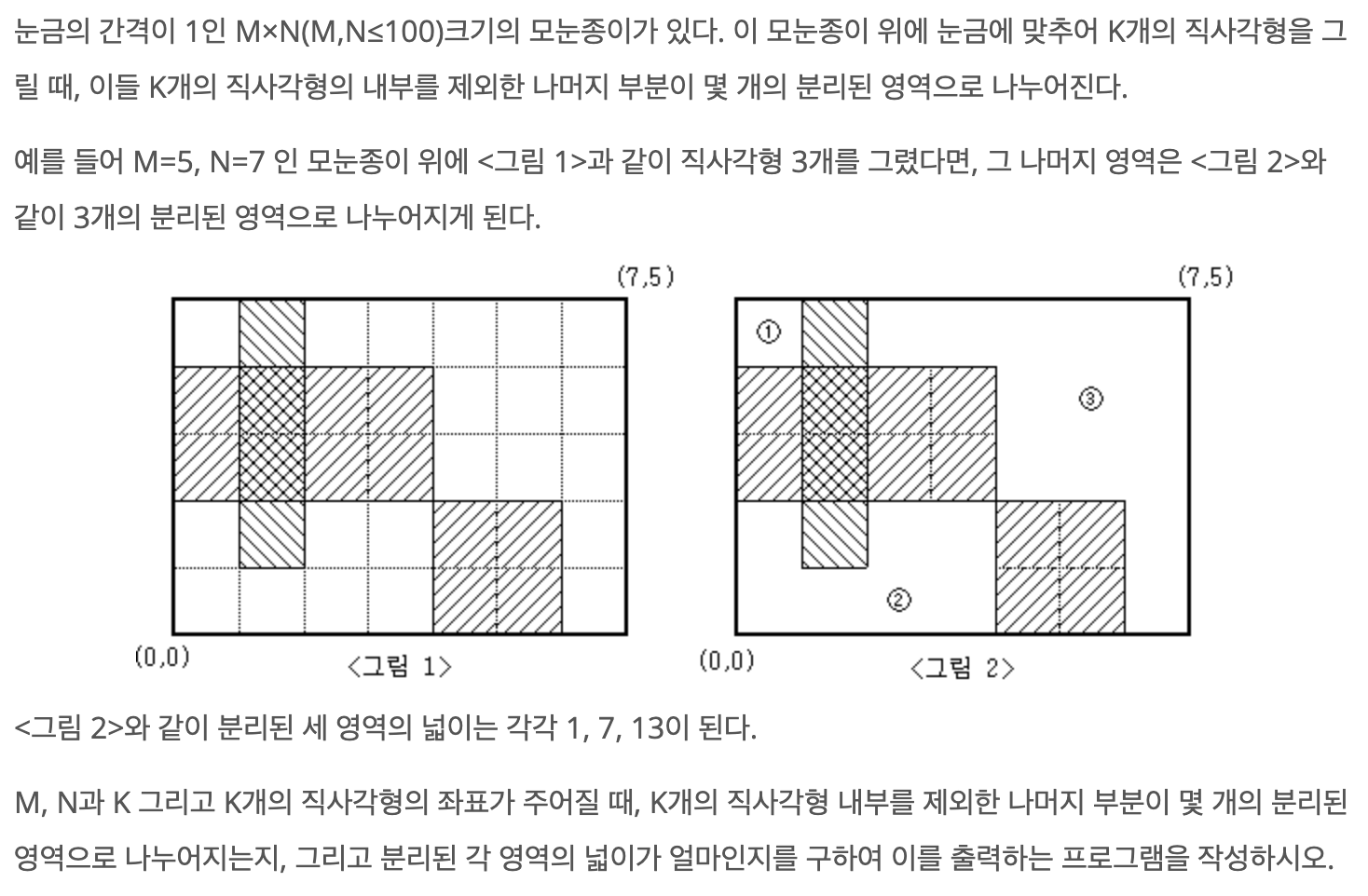
첫째 줄에 M과 N, 그리고 K가 빈칸을 사이에 두고 차례로 주어진다. M, N, K는 모두 100 이하의 자연수이다. 둘째 줄부터 K개의 줄에는 한 줄에 하나씩 직사각형의 왼쪽 아래 꼭짓점의 x, y좌표값과 오른쪽 위 꼭짓점의 x, y좌표값이 빈칸을 사이에 두고 차례로 주어진다. 모눈종이의 왼쪽 아래 꼭짓점의 좌표는 (0,0)이고, 오른쪽 위 꼭짓점의 좌표는(N,M)이다. 입력되는 K개의 직사각형들이 모눈종이 전체를 채우는 경우는 없다.

출력

첫째 줄에 분리되어 나누어지는 영역의 개수를 출력한다. 둘째 줄에는 각 영역의 넓이를 오름차순으로 정렬하여 빈칸을 사이에 두고 출력한다.

예제

문제 정의

이 문제를 처음 풀었을 때 예제의 결과와 다르게 나와서 당황했다.

m,n이 주어졌을 때, 자연스래 가로, 세로 순으로 주어졌으리라 생각하고 m, n을 반대로 생각해 풀었기 때문이었다.. 문제를 꼼꼼히 읽도록 하자!

이 문제의 경우 주어진 두 좌표사이의 영역을 1로 칠하고 1로 칠해져있지 않은 부분의 연결요소 개수와 각 연결요소의 너비를 구하는 식으로 풀었다.

연결요소이므로 dfs를 돌렸고 각 연결요소의 너비는 각 빈 공간과 연결되어 있는 빈공간의 개수를 구하기 위해 dfs의 내부 dfs를 호출할 때마다 1씩 반환하여 size 변수에 더해나갔다.

그 후 연결요소 너비를 담는 res에 담고 sort한 후 차례로 출력했다

#include<bits/stdc++.h>
using namespace std;
int m, n, k, adj[104][104], visited[104][104];
int a, b, c, d, cnt;
vector<int> res;
const int dy[4] = {-1, 0, 1, 0};
const int dx[4] = {0,1,0,-1};

int dfs(int y, int x) {
  visited[y][x] = 1;
  int size = 1;
  for (int i = 0; i < 4; i++) {
    int ny = y + dy[i];
    int nx = x + dx[i];
    if (ny<0 || ny >= m || nx<0 || nx>=n || visited[ny][nx] || adj[ny][nx]) continue;
    size += dfs(ny, nx);
  }
  return size;
}
int main() {
  cin >> m >> n >> k;
  for (int i = 0; i < k; i++) {
    cin >> a >> b >> c >> d;
    for (int t = b; t < d; t++) {
      for (int r = a; r < c; r++) {
        adj[t][r] = 1;
      }
    }
  }

  for (int i = 0; i < m; i++) {
    for (int j = 0; j < n; j++) {
      if(!visited[i][j] && adj[i][j] == 0) {
        res.push_back(dfs(i, j));
        cnt++;
      }
    }
  }
  cout << cnt << "\n";
  sort(res.begin(), res.end());
  for (int i : res) {
    cout << i << " ";
  }
  return 0;
}