코드를 참고한 기술 블로그
문제 간략히 설명하자면
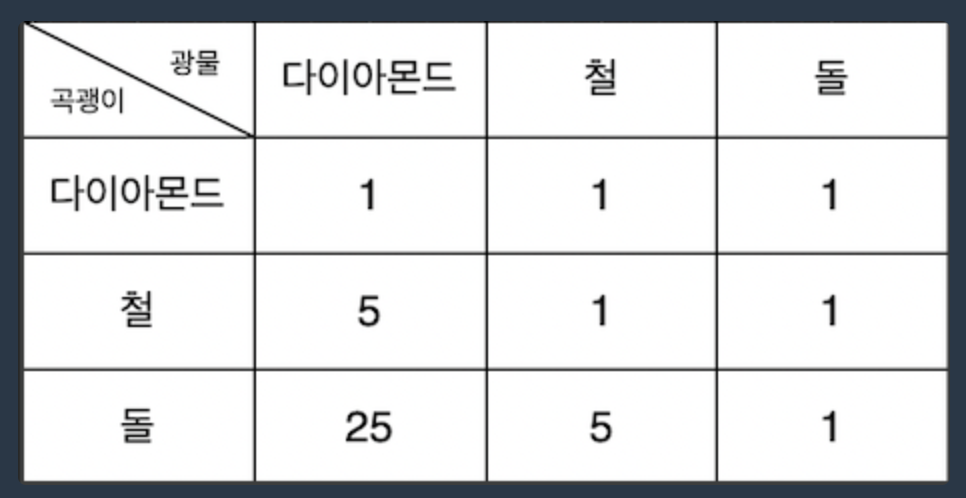
곡괭이마다 각 광물을 캘 때 드는 피로도는 위의 표와 같다.
각 곡괭이는 종류에 상관없이 광물 5개를 캔 후에는 더 이상 사용할 수 없다.
-
사용할 수 있는 곡괭이중 아무거나 하나를 선택해 광물을 캔다.
-
한 번 사용하기 시작한 곡괭이는 사용할 수 없을 때까지 사용한다.
-
광물은 주어진 순서대로만 캘 수 있다.
-
광산에 있는 모든 광물을 캐거나, 더 사용할 곡괭이가 없을 때까지 광물을 캔다.
목표는 전체 광물 채취에 필요한 피로도 총합을 최소화하는 것이다.
문제정의
처음에는 피로도 표를 봤을 때 다이아몬드 -> 철 -> 돌 순서로 곡괭이를 사용하면 최소피로도 요건을 충족할 수 있을 것이라 생각했다.
하지만 계속 시도했으나 정확도 42.9에 머물고 나아지질 않았다.
결국 다른 기술 블로그의 도움을 받았는데, 효율적인 곡괭이 순서대로 파는게 최소 피로도를 도출해내지 못한다는 것을 알게되었다.
효율 높은 곡괭이부터 무조건 많이 쓰면, 나중에 고피로도 광물을 약한 곡괭이로 캐야 할 수 있다는 것을 알게되었다.
예를 들어 앞서, 광물 돌이 연속해서 나와서 다이아몬드 곡괭이를 전부 소진했는데 뒤에 다이어몬드 광물이 연속해서 나오게된다면 하는 수 없이 다이아몬드를 캐는데 가장 큰 피로도가 드는 돌 곡괭이로 다이아몬드를 캐야되는 것이다.
따라서 효율성이 높은 순서대로 곡괭이를 쓰는 것은 옳지않다. 뒤에 어떤 광물이 나올지 모르기 때문이다.
그래서 모든 곡괭이 사용 순서를 DFS로 탐색하여 가능한 경우의 수를 모두 확인했다.
피로도 표를 fatigue라는 2차원배열에 미리 저장해놓았고, 캐야할 광물이 배열로 주어지기 때문에 각 광물 명에 인덱스 번호를 부여했다.
map<string, int> m;
m.insert({"diamond", 0});
m.insert({"iron", 1});
m.insert({"stone", 2});
int fatigue[3][3] = {{1,1,1}, {5,1,1}, {25,5,1}};모든 곡괭이를 사용하는 경우의 수를 구하기 위해 dfs 함수를 작성했다.
기저 조건은 현재 탐색하는 광물의 위치가 전체 광물의 개수와 같을 경우, 혹은 모든 곡괭이를 소진했을 경우이다.
이때 피로도의 최솟값을 리턴한다.
각 곡괭이로는 최대 5개의 광물을 캘 수 있으므로 for문을 돌며 피로도를 합산해주고 dfs를 돌린다.
void dfs(vector<int> &picks, vector<string> &minerals, int sum, int loc, int &answer) {
if (loc == minerals.size() || picks[0]==0 && picks[1]==0 && picks[2]==0) {
answer = min(answer, sum);
return;
}
// 모든 곡괭이를 사용하는 경우의 수
for(int i=0; i<3; i++) {
if (picks[i]!=0) {
picks[i]--;
int tmpidx = loc;
int tmpsum = sum;
for(; tmpidx<loc+5 && tmpidx<minerals.size(); tmpidx++) {
tmpsum += fatigue[i][m[minerals[tmpidx]]];
}
dfs(picks, minerals, tmpsum, tmpidx, answer);
picks[i]++;
}
}
}[전체 코드]
#include <string>
#include <vector>
#include <algorithm>
#include <map>
using namespace std;
map<string, int> m;
int fatigue[3][3] = {{1,1,1}, {5,1,1}, {25,5,1}};
void dfs(vector<int> &picks, vector<string> &minerals, int sum, int loc, int &answer) {
if (loc == minerals.size() || picks[0]==0 && picks[1]==0 && picks[2]==0) {
answer = min(answer, sum);
return;
}
// 모든 곡괭이를 사용하는 경우의 수
for(int i=0; i<3; i++) {
if (picks[i]!=0) {
picks[i]--;
int tmpidx = loc;
int tmpsum = sum;
for(; tmpidx<loc+5 && tmpidx<minerals.size(); tmpidx++) {
tmpsum += fatigue[i][m[minerals[tmpidx]]];
}
dfs(picks, minerals, tmpsum, tmpidx, answer);
picks[i]++;
}
}
}
int solution(vector<int> picks, vector<string> minerals) {
int answer = 50*25;
m.insert({"diamond", 0});
m.insert({"iron", 1});
m.insert({"stone", 2});
dfs(picks, minerals, 0, 0, answer);
return answer;
}