재귀함수
재귀(Recursion) : 어떠한 것을 정의할 때 자기 자신을 참조하는 것을 뜻한다.
재귀함수 : 종료조건이 참이 될때까지 스스로를 계속 호출시켜 반복하는 함수
재귀함수는 for문이나 while문 등의 반복문으로도 대체가 가능하다. 재귀함수는 메모리를 많이 차지하기 때문에 문제에 따라 반복문을 이용하는 것이 더 유리할 때도 있다.
1)함수를 반복 호출하며 스택 메모리가 커지고 스택오버플로우가 발생할 수 있고 2)스택 프레임을 구성하고 해제하는 과정때문에 반복문보다 성능도 느리다. (+ 기존 재귀의 메모리와 성능 문제를 보완하는 꼬리 재귀이란 개념도 있긴하다.)
그럼 왜 재귀함수를 사용하는 것일까?
재귀함수를 사용하는 이유
- 알고리즘 자체가 재귀적인 표현이 자연스러운 경우 재귀함수를 이용하면 직관적인 코드를 작성할 수 있다.
- 변수 사용을 줄일 수 있다. 즉, mutable state(변경 가능한 상태)를 줄여 프로그램의 오류 가능성을 낮춘다.
사용 시 유의사항
- 자신을 호출한 후 그 함수가 끝날 때까지 함수 호출 이후의 명령문이 수행되지 않는다
- 무한 반복되지 않도록 종료 조건을 설정해야 한다.
예시 1 : 팩토리얼
팩토리얼 1부터 양의 정수 n까지의 모든 정수를 곱한 것을 의미
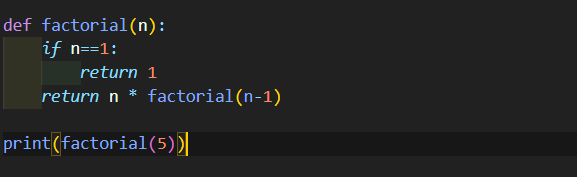
3! = 3*2*1, 4! = 4*3*2*1,5! = 5*4*3*2*!
5!은 5*4!, 5*4*3! 로도 표현이 가능하다. 즉, 팩토리얼에는 n*(n-1)!이라는 규칙이 있으므로 재귀함수를 통해 간단하게 표현이 가능하다. 탈출조건이 없다면 무한 반복되므로 n==1일 때 함수를 종료시킨다.
예시 2 : 회문문
회문 거꾸로 읽어도 똑같이 읽히는 것을 의미
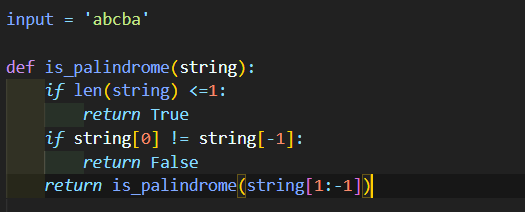
가운데 글자를 중심으로 대칭된다는 특징이 있기 때문에 앞에서 n번째 글자와 뒤에서 n번째 글자는 동일하다. 이를 string[0] != string[-1]이라는 식으로 비교해주었고 일치한다면 그 다음 문자들을 비교하기 위해 비교할 문자열의 범위를 축소하여 재귀함수에 투입하였다. 재귀함수가 반복 호출되다 문자열이 하나만 남게 되면 더 이상 비교할 문자가 없을 때까지 모든 문자들이 동일했다는 것이므로 회문문이 맞다는 의미로 True를 반환하고 함수를 종료시킨다.
예시 3 : 하노이의 탑
하노이의 탑은 아동 교구에서 본 적이 있다. 규칙은 아래와 같다.

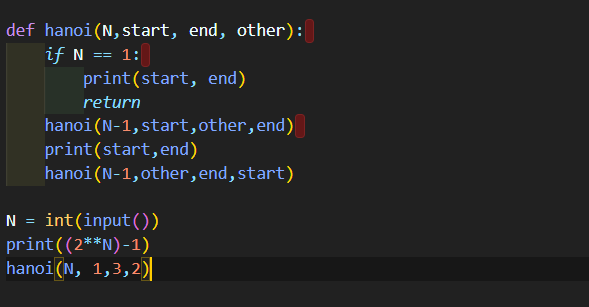
만족스러울만큼 이해하기까지 오랜 시간이 걸렸고 덕분에 재귀함수에 대해 깊이 생각해볼 수 있던 문제였다. 하노이의 탑의 규칙은 최종적으로 옮기고자 하는 기둥에 맨 마지막 원판이 위치해야 한다는 것이다. 원판들은 한 번에 하나씩밖에 이동할 수 없다보니 보조기둥과 주기둥을 번갈아가는 과정을 반복하며 최종 목적지 기둥에 쌓이게 된다. 하노이의 탑은 알고리즘 풀이로 다시 한 번 올릴 예정이다.
참고자료
재귀함수를 쓰는 이유 : 재귀함수의 단점과 그럼에도 사용하는 이유를 이해하는데 도움이 되었다.
재귀함수에 대한 질문입니다. : 질문에 달린 댓글들을 통해 재귀함수를 사용하는 이유를 생각해보게 된다.
하노이의 탑(재귀알고리즘) : 코드 설명이 매우 상세하다.
하노이 탑 이동 순서 : 코드 흐름이 그림으로 표현되어 있다.
개념이해 재귀함수 : '열고 들어온 문을 닫으며 나간다'는 비유덕에 재귀함수 개념을 이해하기 한결 편했다.
심화
재귀함수는 왜 어려울까 : DP, 스택 등은 공부한 뒤에 읽으면 재귀를 쓰면 좋은 점을 이해할 수 있을 것 같다.

