
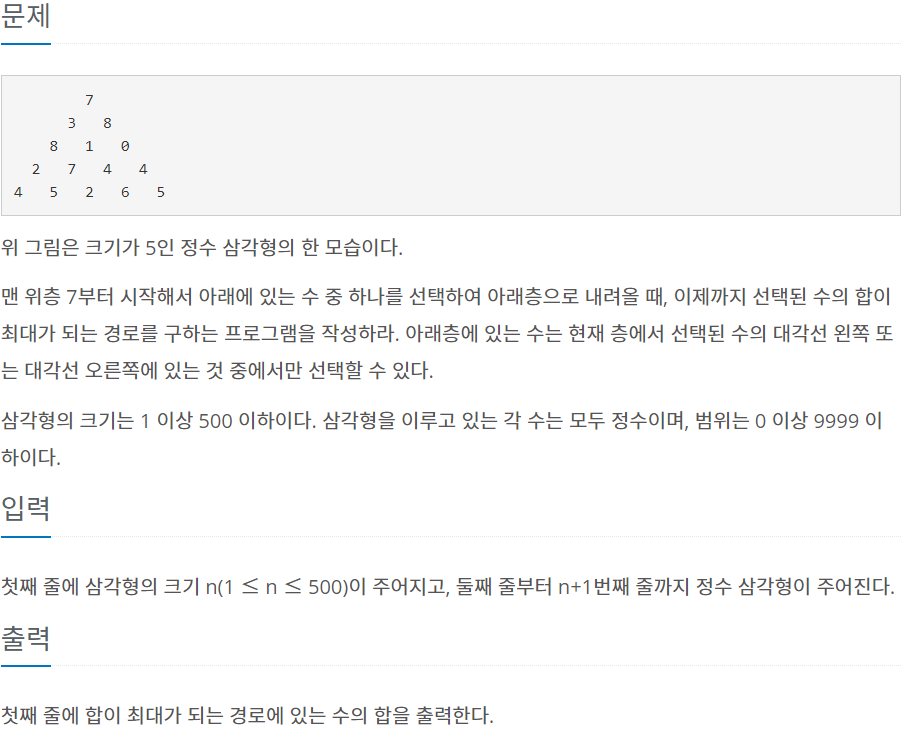
문제해석
이동경로의 수를 더한 값이 최대가 될 때 그 수를 출력해야 한다.
접근방식
- Dynamic Programming 적용 : n은 n-1번까지 계산한 수 중 최대값과 합산하여 값을 누적해나간다.
- 대각선으로 연결된 값만 합산이 가능한데 이 조건을 어떻게 구현하면 좋을까?
- 삼각형 가장자리의 수들은 내부에 위치한 수와 달리 합산할 수 있는 선택지가 하나 뿐이다.
- 대각선 이동이 가능한 것은 안쪽에 존재하는 값들이다.
- 반복되는 연산 안에서 조건을 달리 주어야한다.
코드설계
- 아래로 갈수록 1씩 증가하는 삼각형 형태의 배열 생성
- 배열 인덱스는 정삼각형 모양이 아니기에 대각선 값 매칭 시 인덱스 값 지정에 유의
- 삼각형 가장자리 수(리스트의 양 끝 값)는 선택지가 1개
- 내부에 위치한 수는 선택지가 2개이고 그 중 큰 값을 선택하도록 조건문 설계
정답코드
import sys
n = int(sys.stdin.readline())
#입력 값을 한 줄씩 배열에 저장
triangle_value = [list(map(int,sys.stdin.readline().split())) for _ in range(n)]
rst = []
#계산 값을 저장하기 위한 삼각형 구조 배열 생성
for i in range(1, n+1): # 내부 반복문의 범위가 되므로 1부터 시작하자.
rst.append([0 for _ in range(i)])
for i in range(n):
if i == 0:
rst[0][0] = triangle_value[0][0]
else:
for j in range(i+1):
#j의 위치에 따른 조건문
if j == 0: #삼각형의 왼쪽 가장자리
rst[i][j] = rst[i-1][j]+triangle_value[i][j]
elif j == i: #삼각형의 오른쪽 가장자리
rst[i][j] = rst[i-1][j-1]+triangle_value[i][j]
else:
rst[i][j] = max(rst[i-1][j-1],rst[i-1][j])+triangle_value[i][j]
print(max(rst[n-1]))
코드설명
길이가 하나씩 증가하는 2차배열이 사용되었다. 시각화해보았다.
-
입력값을 저장하는 배열이다.
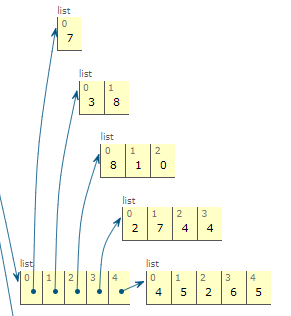
-
결과 값을 저장하기 위한 배열이다.
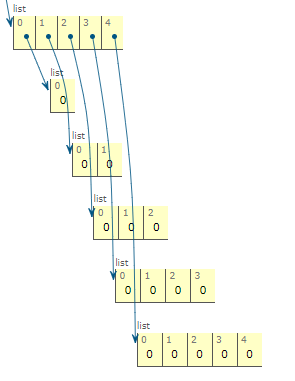
n-1번째 계산 결과를 이용하여 n을 계산하는 반복문
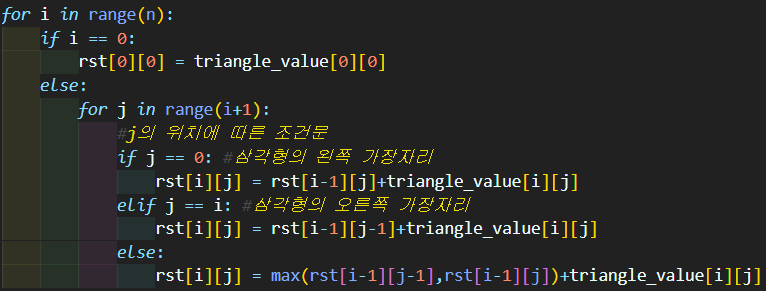
수의 자리가 삼각형의 가장자리인지 아닌지를 판단한다. 가장자리라면 좌측(j == 0)인지 우측(j == i)인지에 따라 합산할 값의 인덱스를 지정해주고 가장자리가 아닌 수라면 합산할 수 있는 선택지가 두 개 주어지므로 그 중 큰 값을 선택해 합산하도록한다. 인덱스 값을 주의해서 넣지 않으면 틀리기 쉽다.
문제에서 요구하는 조건에 따라 출력한다.

결국 rst 리스트 가장 하단 행(rst[n-1])에는 모든 계산을 마치고 누적된 값들이 저장되어있다. 그 값들 중에서도 가장 큰 값을 찾아 출력하면 된다.
