
접근방식
소수를 구하고 n보다 크고 2n보다 같거나 작은 범위를 추려 개수를 출력한다.
📑 코드풀이

- 입력 :
테스트 케이스는 한 줄씩 입력받아야하며 0은 종결을 의미한다. 탈출조건은 n==0으로 둔 while문을 통해 한 줄씩 입력받았다. 입력된 값들은 배열에 저장했다. 입력값들을 배열에 저장하지 않고 for문 내에 계산식을 구현하여 값을 출력해도 되나 그렇지 않은 이유는 소수를 구하는 함수의 결과값을 재활용하여 반복을 줄이기 위해서이다.
-
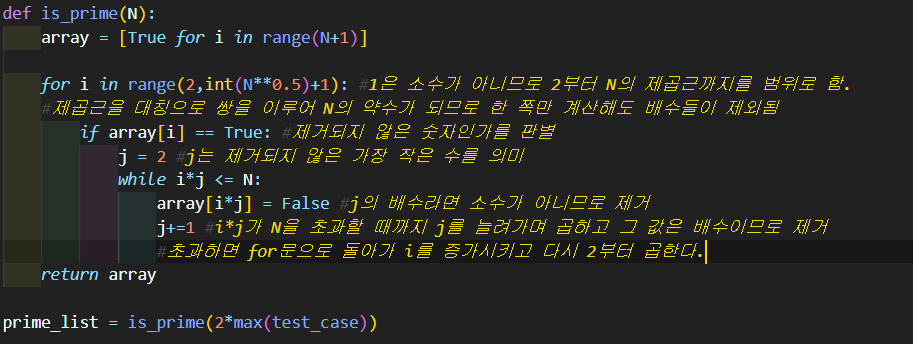
소수 판별 함수:
에라토스테네스의 체 방식을 이용하여 1을 제외한 가장 작은 수의 배수를 지워나갈 것이다.
array 생성:
1부터 N까지의 배열을 만든다. 소수가 아닌 수를 지워나가기 위해 초기값은 모두 True로 설정한다. 숫자와 인덱스를 일치시키기 위해 범위를 n+1로 늘렸다.
반복문:
array[i]에는 i라는 수가 소수인지 아닌 지에 대한 boolean 값이 저장되어 있다. 이 인덱스를 반복문으로 돌리며 소수 여부를 판단할 것이다. 이 때 반복하는 범위가2 ~ int(N**0.5)+1인데 의미는 아래와 같다.1은 소수가 아니므로 1을 제외한 가장 작은 수인 2부터 시작한다.
N**0.5는 N의 0.5승, 제곱근을 의미한다. 범위를 제곱근까지 제한하는 이유는 1부터 N까지의 수를 나열했을 때 N의 제곱근을 기준으로 대칭되는 수들이 N의 약수(약수의 법칙) 가 되기 때문이다. N의 제곱근보다 작은 수로도 배수들이 모두 제거되기 때문에 N의 제곱근보다 큰 수를 기준으로 반복문을 돌려도 제거할 수가 남아있지 않아 의미가 없다.if array[i] == True:
해당 값이 True라는 의미는 아직 제거되지 않았다는 것이므로 종속된 코드를 실행한다. 이미 제거된 수라면 다음 i로 넘어간다.
while i*j ≤=N:
i라는 수와 j (배열에 잔존하는 수 중 가장 작은 수)의 곱이 N을 초과할 때까지 반복한다. 반복문에 j를 1씩 증가시키는 코드가 있으므로 i*j의 곱이 N을 넘지 않는 범위 안에서 j는 계속 증가하여 j의 배수를 모두 False로 바꾼다.

- 함수는 1번만 호출한 뒤 재사용한다.
소수를 구하는 함수는 입력된 테스트 케이스 중 가장 큰 수(max(test_case))의 범위(2*n = 2*max(test_case))를 기준으로 하여 계산한다. 그렇게 해야 다른 테스트 케이스에도 활용할 수 있다.

- 출력:
test_case별로 소수의 개수를 구할 것이다. 소수의 개수를 세는 num_of_prime 변수는 각 test_case마다 초기화 해주어야 정확한 값이 계산된다. 누적되거나 다른 test_case에 영향을 주면 안 된다.
문제에서 주어진 n보다 크고 2n보다 작거나 같은 조건에 따라 for문의 범위를 지정해주고 해당 숫자가 소수이고 1이 아니라면 소수의 개수를 증가시켜주었다. 한 테스트 케이스 안에 소수 개수를 카운트하는 반복문이 종료되면 결과를 출력하고 다음 테스트 케이스도 동일하게 반복한다.
정답코드
test_case = []
while True:
n = int(input())
if n == 0:
break
test_case.append(n)
def is_prime(N):
array = [True for i in range(N+1)]
for i in range(2,int(N**0.5)+1):
if array[i] == True:
j = 2
while i*j <= N:
array[i*j] = False
j+=1
return array
prime_list = is_prime(2*max(test_case))
for n in test_case:
num_of_prime = 0
for i in range(n+1,2*n+1): #입력값 범위 내에서만 출력되도록 지정
if prime_list[i] and i!=1: #1은 소수가 아니므로 제외
num_of_prime +=1
print(num_of_prime)
