🪜 백준 No.10844 쉬운 계단 수

🔗 https://www.acmicpc.net/problem/10844

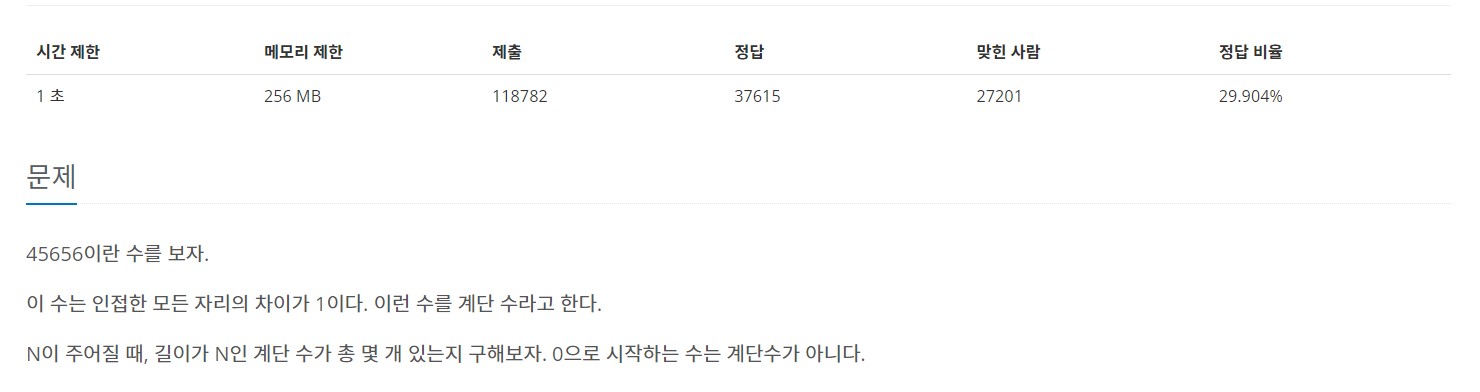
1. 문제

2. 입출력

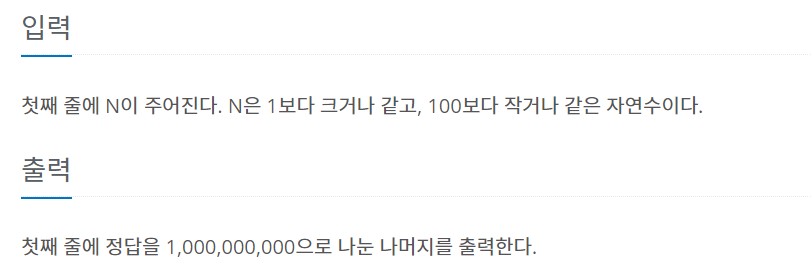
• 입력 예시1
  1

• 출력 예시1
  9

• 입력 예시2
  2

• 출력 예시2
  17

---

3. ❌ 오답 문제 풀이

• 'Dynamic Programming'의 'Top Down' 방식 사용
  : 재귀 함수 -> 쉬운 이해, 시간의 제약

• Stack을 사용하여 자릿수를 dfs처럼 재귀법으로 구현

4. ❌ 오답 코드

package StairCnt_10844;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Stack;

public class Sub_TopDown {
    private static int N;
    private static int mod = 1000000000;
    private static int cnt = 0;
    private static void calc(Stack<Integer> st) {
        if(st.size() >= N) {
            cnt++;
            return ;
        }
        if(st.peek() > 0) {
            st.push(st.peek() - 1);
            calc(st);
            st.pop();
        }
        if(st.peek() < 9) {
            st.push(st.peek() + 1);
            calc(st);
            st.pop();
        }
    }

    public static void main(String[] args) throws IOException {
        long startTime = System.currentTimeMillis();
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine());

        Stack<Integer> stack = new Stack<>();
        for (int i = 1; i <= 9; i++) {
            stack.push(i);
            calc(stack);
            stack.pop();
        }

        if(cnt != 0) {
            System.out.println(cnt % mod);
        }
    }
}

---

5. ⭕ 정답 문제 풀이

• 'Dynamic Programming'의 'Bottom Up' 방식 사용
  : for문 -> 시공간 절약

• 자릿수에 해당하는 숫자들이 존재하는 개수를 저장. (Memoization이라고 생각)

• 코드에서 중간에 나머지 계산을 해주는 이유
  : 점화식을 통해 합을 계산하는 경우에도, type 범위를 초과해서 원치 않는 값을 배열에 저장하는 경우가 발생하기 때문
  (범위를 초과하여 음수 값이나 쓰레기 값이 저장됨)

---

ex) dp[3][5] = dp[2][4] + dp[2][6]
: 2번째 자릿수가 4인 수와 2번째 자릿가 6인 수들이 3번째 자릿수에 5를 넣을 수 있기 때문

6. ⭕ 정답 코드

※ dp[i][j]
- i : 자릿수
- j : 숫자
- dp[i][j] : i 자릿수에 j라는 수가 있는 총 개수

ex) dp[3][5] => XX5 (345, 765, ...)

import java.util.Scanner;

public class Main {
    static int N;
    static long mod = 1000000000;
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        N = sc.nextInt();
        long dp[][] = new long[N+1][10];

        for(int i=1; i<10; i++) {
            dp[1][i] = 1;
        }

        for(int i = 2; i <= N; i++) {
            for(int j = 0; j < 10; j++) {
                long add = 0;

                if(j + 1 <= 9) add += dp[i - 1][j + 1];
                if(j - 1 >= 0) add += dp[i - 1][j - 1];

                dp[i][j] = add % mod;
            }
        }

        long ans = 0;
        for(int i=0; i<10; i++) {
            ans += dp[N][i];
        }

        System.out.println(ans % mod);
    }

}

---

7. ✅ Top Down 방식 오답 이유

• Time Over

• Top Down 방식을 사용하여 자릿 N이 커질수록 함수의 깊이도 늘어남에 따라 Bottom Up 방식으로 해결

✔️ Dynamic Programming 시간 복잡도
◻ Top Down
   : O(2^N)
◻ Bottom Up
   : O(N^2)