0. 공부 배경

---

LLM을 구동하기 위해 엔진을 찾아보니 생각보다 많은 종류가 있다
대충 둘러본 내용은 아래와 같은데..

엔진 이름	장점	GitHub Stars (24.06)
LLaMA.C++	호환성 (C++)	60.7K
ExLlama	단일 처리 속도	2.7K + 3.2K
vLLM	병렬 처리 속도	21.6K

이 외에도 TensorRT-LLM 등 다양한 엔진이 있는 듯 하다

모든 기술을 다 이해할 필요는 없지만, 자신에게 필요한 지식은 공부할 필요가 있다고 생각한다
예를 들어 내가 여러 사용자가 물리는 서비스에 LLM을 서빙해야한다면, 병렬처리가 장점인 vLLM을 고려해볼 것이다.

다양한 엔진에서 Paged Attention이니 Flash Attention이니 다양한 기법들이 적용되어가고 있는데
원리를 이해하고 있어야 시스템에서 효과적일지 알 수 있을 것 같아서 차근차근 공부하고자 한다

1. Attention

---

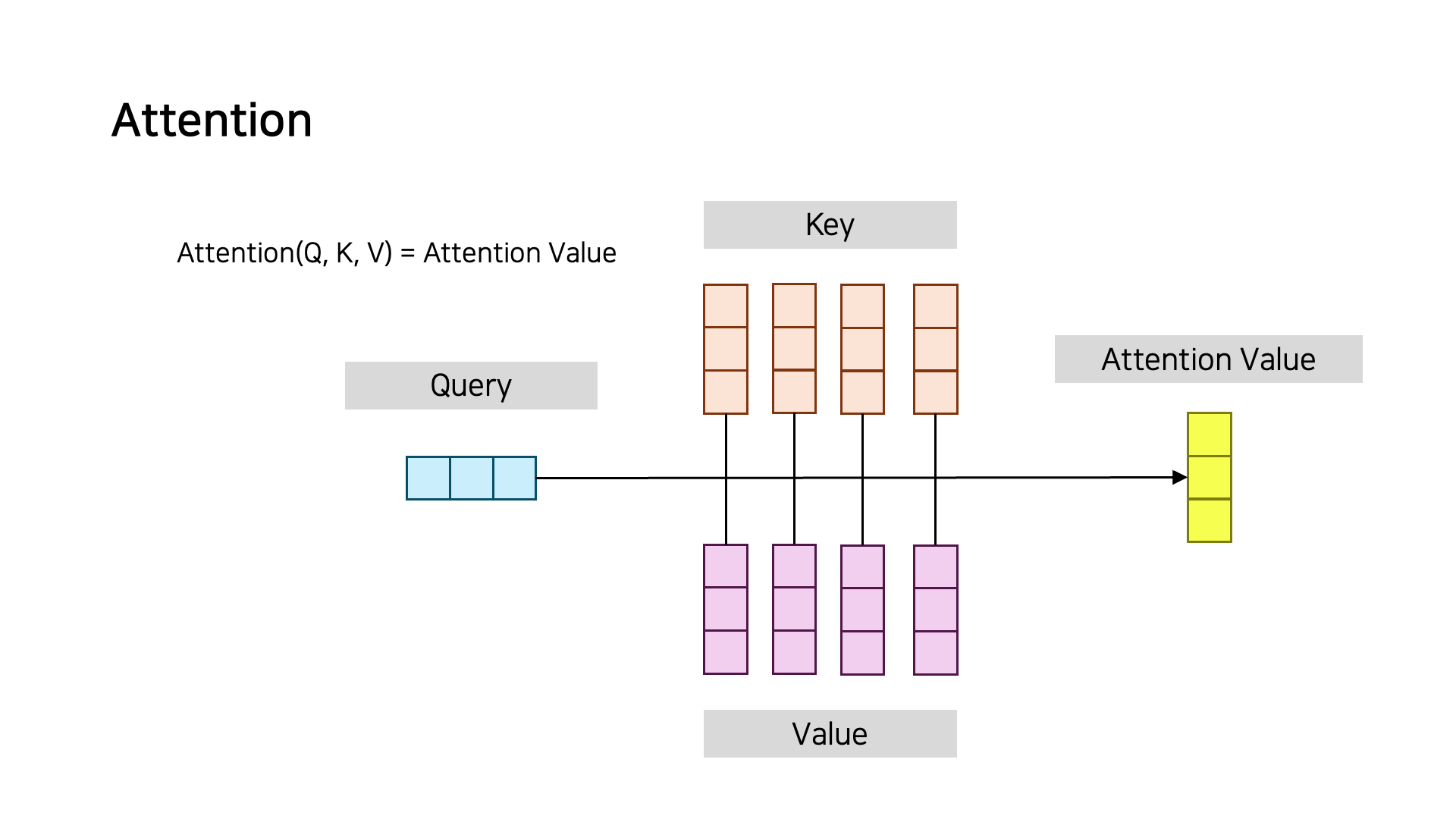Attention 메커니즘은 기본적으로 Q, K, V로 Attention Value를 구하게 된다 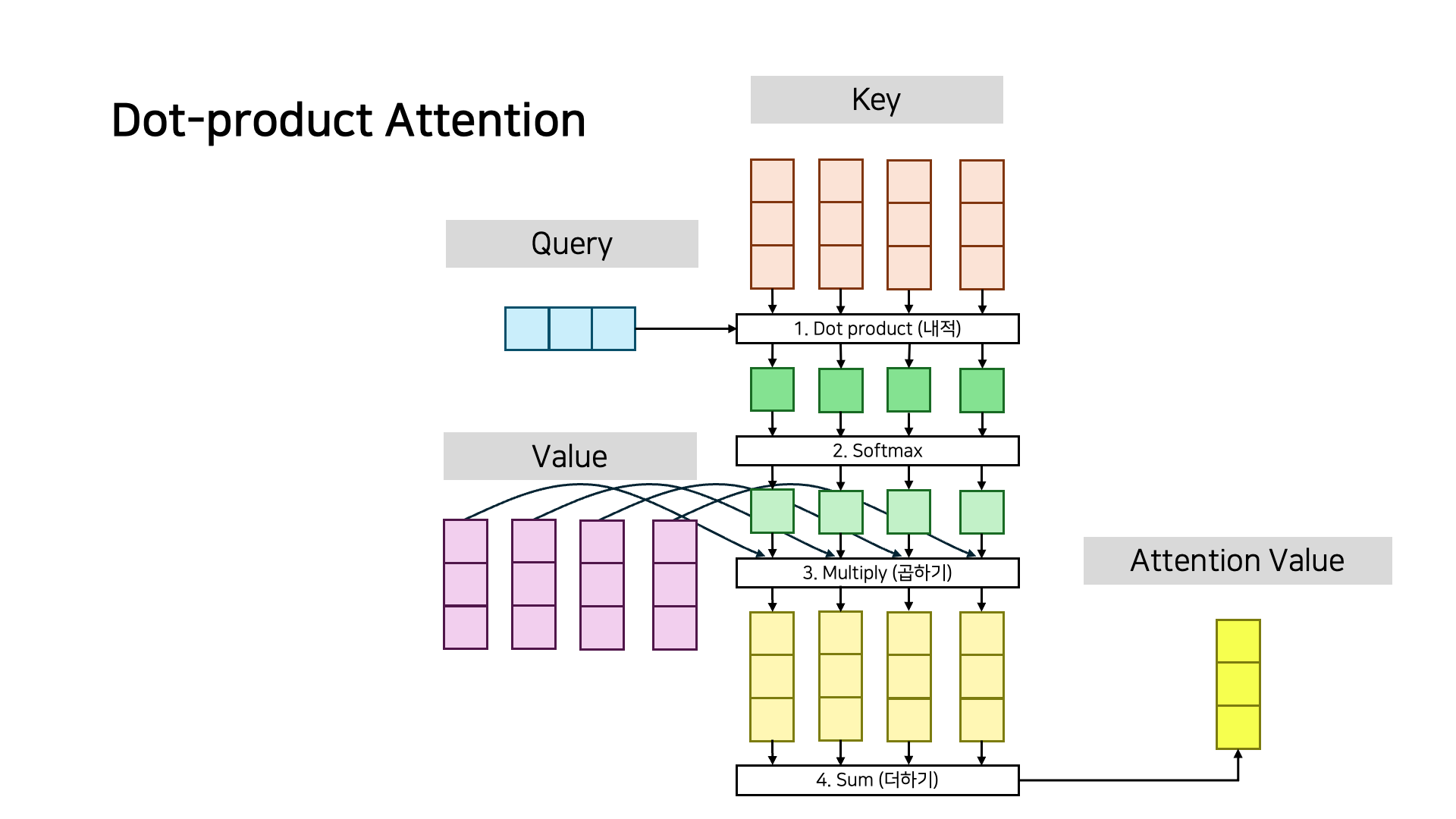예를 들어 Dot-product Attention은 위와 같이 연산되는데
실제로는 쿼리가 여러개이므로 행렬 연산이 이루어진다 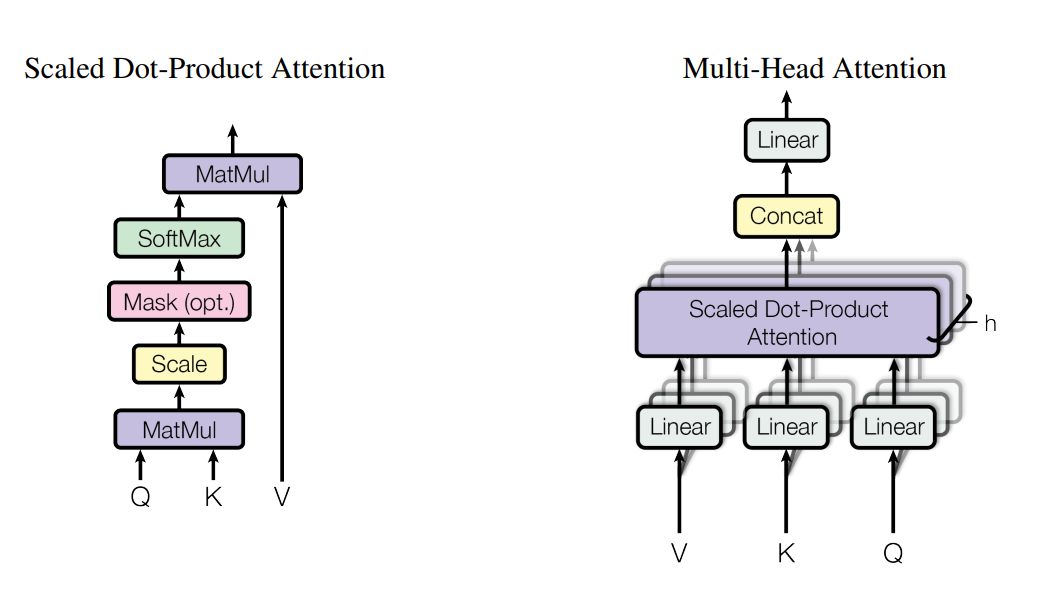Transformer 모델에서는 Scale 과정이 추가된 Scaled Dot-Product Attention을
여러개 겹쳐놓은 Multi-Head Attention을 사용한다고 한다

아무튼 Attention(Q, K, V) 함수는 Q, K, V로 열심히 행렬 연산을 수행하는 것이다.

Attention 메커니즘 이해에 도움이 될만한 자료들

• 위키독스 (딥 러닝을 이용한 자연어 처리 입문)
  • Attention
  • Transformer
• 블로그 (codingopera)
• Transformer paper

2. Flash Attention

---

• We propose FlashAttention, a new attention algorithm that computes exact attention with far fewer memory accesses.
• 우리는 FlashAttention이라는 새로운 Attention 알고리즘을 제안합니다.
• 이 알고리즘은 훨씬 적은 메모리 접근으로 정확한 Attention을 계산합니다.

• Even with the increased FLOPs due to recomputation, our algorithm both runs faster and uses less memory than standard attention, thanks to the massively reduced amount of HBM access
• 재계산으로 인해 FLOP(부동소수점 연산 수)가 증가했음에도 불구하고, 우리의 알고리즘은 Standard Attention보다 빠르게 실행되고 메모리를 적게 사용합니다.
• 이는 HBM 접근을 크게 줄였기 때문입니다.

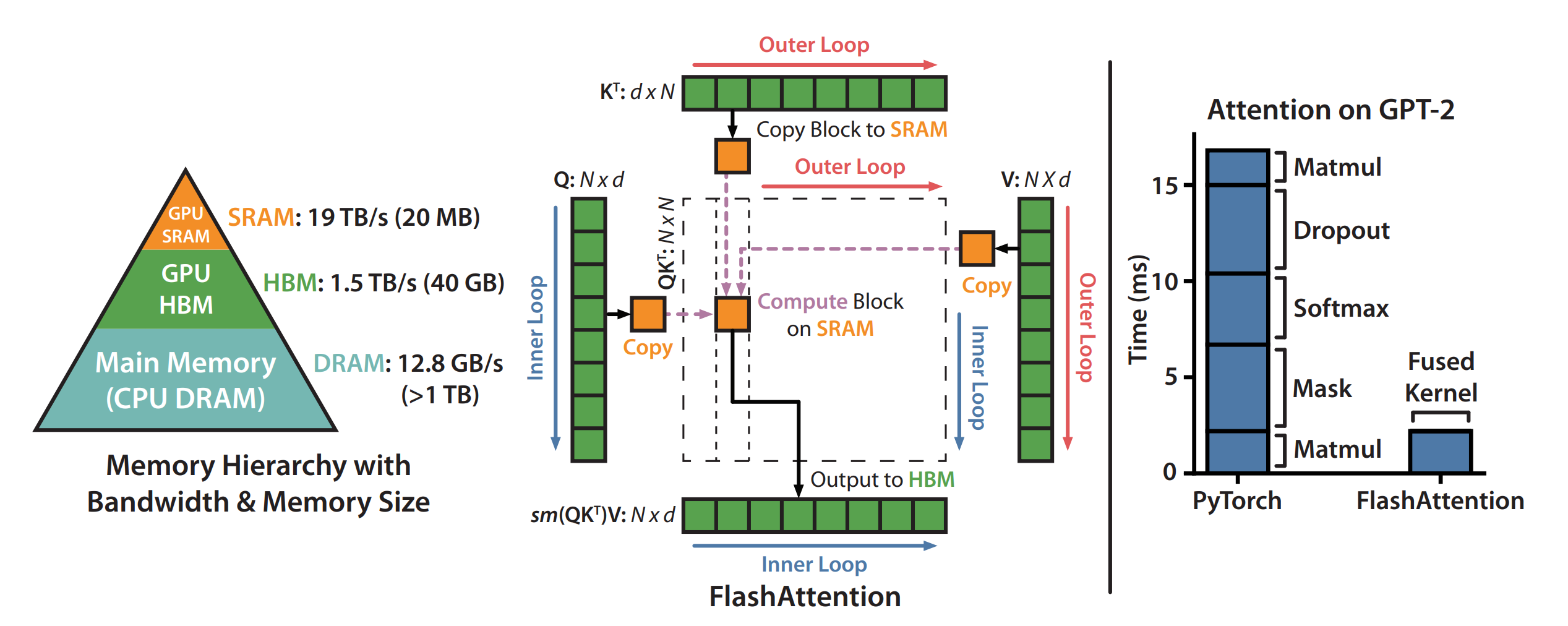
논문에 따르면 HBM 접근 빈도를 줄여서, 연산 횟수는 늘었음에도 빠르게 만들었다고 한다.

의사코드

$\text{Require: Matrices } Q, K, V \in \mathbb{R}^{N \times d} \text{ in HBM, on-chip SRAM of size } M.$
$N : \text{입력 토큰 수, }d : \text{임베딩 차원 수}$
1. $\text{블록 크기를 SRAM이 허용하는 범위에서 정의 : } B_c = \left\lceil \frac{M}{4d} \right\rceil, B_r = \min \left( \left\lceil \frac{M}{4d} \right\rceil, d \right).$
$\text{만약 SRAM이 허용해서, }B_r=d\text{이 된다면 } B_c : \text{한번에 처리가능한 토큰 수}$
2. $\text{Output배열 초기화 } O = (0)_{N \times d} \in \mathbb{R}^{N \times d}, \ell = (0)_N \in \mathbb{R}^N, m = (-\infty)_N \in \mathbb{R}^N \text{ in HBM.}$
3. $\text{Q를 } T_r = \left\lceil \frac{N}{B_r} \right\rceil \text{개의 블록 } Q_1, \ldots, Q_{T_r} \text{로 나누고, K와 V를 } T_c = \left\lceil \frac{N}{B_c} \right\rceil \text{개의 블록 } K_1, \ldots, K_{T_c} \text{ 및 } V_1, \ldots, V_{T_c}, \text{로 나눔. 각 블록 크기 } B_c \times d.$
4. $\text{O를 } T_r \text{개의 블록 } O_i, \ldots, O_{T_r} \text{로 나누고, } \ell \text{를 } T_r \text{개의 블록 } \ell_i, \ldots, \ell_{T_r} \text{로 나누고, } m \text{을 } T_r \text{개의 블록 } m_1, \ldots, m_{T_r} \text{로 나눔.}$
5. $\text{for } 1 \le j \le T_c \text{ do}$
6. $\quad HBM \rightarrow SRAM : K_j, V_j \text{를 로드.}$
7. $\quad \text{for } 1 \le i \le T_r \text{ do}$
8. $\quad \quad HBM \rightarrow SRAM : Q_i, O_i, \ell_i, m_i \text{를 로드.}$
9. $\quad \quad SRAM\text{에서 } S_{ij} = Q_i K_j^T \in \mathbb{R}^{B_r \times B_c} \text{ 계산.}$
10. $\quad \quad SRAM\text{에서 } \tilde{m}_{ij} = \text{rowmax}(S_{ij}) \in \mathbb{R}^{B_r}, \tilde{P}_{ij} = \exp(S_{ij} - \tilde{m}_{ij}) \in \mathbb{R}^{B_r \times B_c} \text{ (포인트별)}, \tilde{\ell}_{ij} = \text{rowsum}(\tilde{P}_{ij}) \in \mathbb{R}^{B_r} \text{ 계산.}$
11. $\quad \quad SRAM\text{에서 } m_{\text{new}i} = \max(m_i, \tilde{m}_{ij}) \in \mathbb{R}^{B_r}, \ell_{\text{new}i} = \exp(m_i - m_{\text{new}i}) \ell_i + \exp(\tilde{m}_{ij} - m_{\text{new}i}) \tilde{\ell}_{ij} \in \mathbb{R}^{B_r} \text{ 계산.}$
12. $\quad \quad \text{HBM에 } O_i \leftarrow \text{diag}(\ell_{\text{new}i})^{-1} (\text{diag}(\ell_i) \exp(m_i - m_{\text{new}i}) O_i + \exp(\tilde{m}_{ij} - m_{\text{new}i}) \tilde{P}_{ij} V_j) \text{ 쓰기.}$
13. $\quad \quad \text{HBM에 } \ell_i \leftarrow \ell_{\text{new}i}, m_i \leftarrow m_{\text{new}i} \text{ 쓰기.}$
14. $\quad \text{end for}$
15. $\text{end for}$
16. $\text{O 반환.}$

정리하면, 블록 사이즈를 잘 정의해서 블록 개수$(T_r)$만큼 HBM에 접근이 일어나게 했는데

• $HBM \rightarrow SRAM : Q_i, O_i, \ell_i, m_i$를 Load
• $HBM \leftarrow SRAM : O_i, \ell_{\text{new}i}, m_{\text{new}i}$를 Write

이는 $\Theta\left(\frac{N^2 d^2}{M}\right)$으로 기존 Attention 메커니즘의 $\Theta(Nd + N^2)$보다 크게 줄었다고 한다

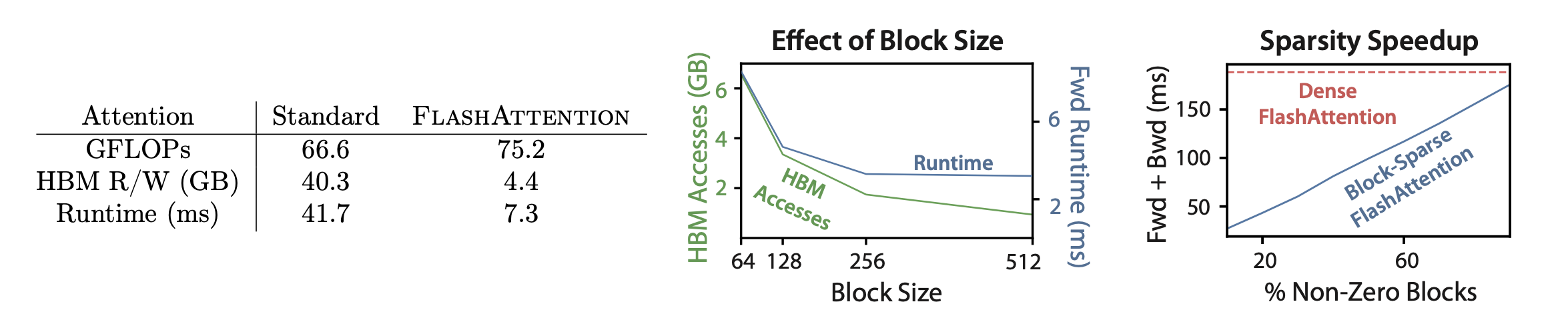
For typical values of $𝑑$ (64-128) and $𝑀$ (around 100KB), $d^2$ is many times smaller than $𝑀$, and thus FlashAttention requires many times fewer HBM accesses than standard implementation. This leads to both faster execution and lower memory footprint, which we validate in Section 4.3.

일반적인 $d$ 값(64-128)과 $M$ 값(약 100KB)에 대해 $d^2$는 $M$보다 훨씬 작습니다. 따라서 FlashAttention은 표준 구현에 비해 HBM 접근 횟수가 훨씬 적습니다. 이는 더 빠른 실행과 더 적은 메모리 사용을 초래하며, 이를 4.3절에서 검증합니다.

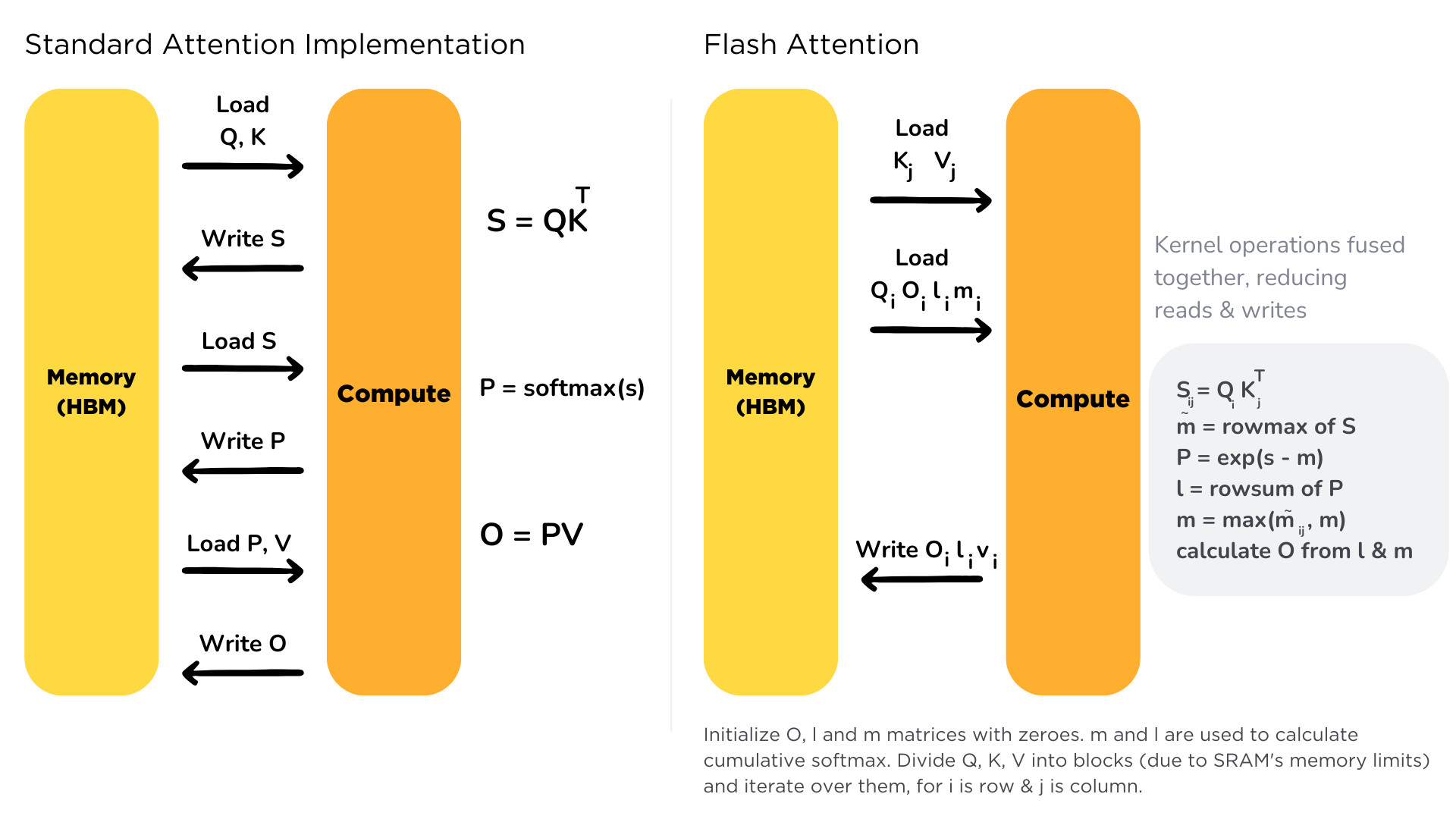
출처 : HuggingFace
그림으로 보면 더 이해하기 쉬운데, 연산량이 늘더라도
HBM의 접근을 최대한 줄여서 시간을 줄였음을 이해할 수 있다.
하드웨어에 따라 성능 변화가 다를 듯하다 (SRAM 크기, 연산 성능 등)