파이썬 알고리즘 058 | 동전 바꿔주기(DFS)

58. 동전 바꿔주기(DFS)

명보네 동네 가게의 현금 출납기에는 k가지 동전이 각각n1, n2, ... , nk개 씩 들어있다.
가게 주인은 명보에게 T원의 지폐를 동전으로 바꿔 주려고한다. 이때, 동전 교환 방법은 여러
가지가 있을 수 있다.예를 들어, 10원 짜리, 5원 짜리, 1원 짜리 동전이 각각2개, 3개, 5개씩
있을 때, 20원 짜리 지폐를 다음과 같은4가지 방법으로 교환할 수 있다.
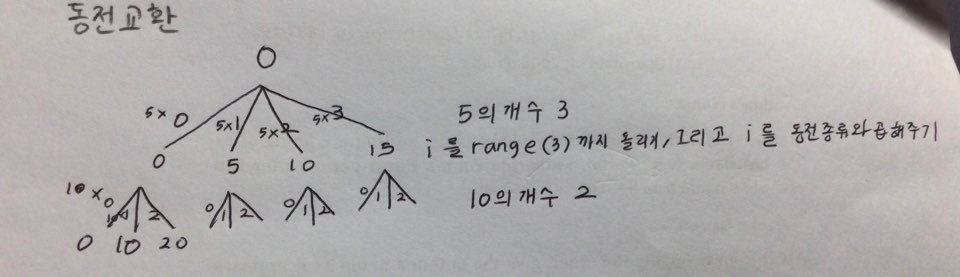
20 = 10×2
20 = 10×1+5×2
20 = 10×1+5×1+1×5
20 = 5×3+1×5
입력으로 지폐의 금액 T, 동전의 가지수 k, 각 동전 하나의금액 pi와 개수 ni가 주어질 때(i=1,2,...,k)지폐를 동전으로 교환하는 방법의 가지 수를 계산하는프로그램을 작성하시오. 방법의 수는 2^31을 초과하지않는 것으로 가정한다.
▣ 입력설명
첫째 줄에는지폐의 금액 T(0<T≤10,000), 둘째 줄에는 동전의 가지 수k(0<k≤10), 셋째 줄부터마지막 줄까지는 각 줄에 동전의금액 pi(0<pi≤T)와 개수 ni(0<ni≤10)가 주어진다. pi와 ni 사이에는 빈 칸이 하나씩 있다.
▣ 출력설명
첫 번째 줄에 동전 교환 방법의 가지 수를 출력한다.(교환할 수 없는 경우는 존재하지 않는다.)
▣ 입력예제 1
20
3
5 3
10 2
1 5
▣ 출력예제 1
4

<내 풀이>

• 이렇게 하면 ch로
  [0, 0, 0, 10, 10, 0, 0, 0, 0, 0][0, 0, 5, 0, 10, 1, 1, 1, 1, 1]
  [0, 0, 5, 10, 0, 1, 1, 1, 1, 1][0, 5, 0, 0, 10, 1, 1, 1, 1, 1]
  [0, 5, 0, 10, 0, 1, 1, 1, 1, 1][0, 5, 5, 0, 10, 0, 0, 0, 0, 0]
  [0, 5, 5, 10, 0, 0, 0, 0, 0, 0][5, 0, 0, 0, 10, 1, 1, 1, 1, 1]
  [5, 0, 0, 10, 0, 1, 1, 1, 1, 1][5, 0, 5, 0, 10, 0, 0, 0, 0, 0]
  [5, 0, 5, 10, 0, 0, 0, 0, 0, 0][5, 5, 0, 0, 10, 0, 0, 0, 0, 0]
  [5, 5, 0, 10, 0, 0, 0, 0, 0, 0][5, 5, 5, 0, 0, 1, 1, 1, 1, 1] 가 나온다

즉, 순서가 바뀌면 다른 걸로 인식을 해서 14개나 나온다
예를 들어 [5, 5, 0, 0, 10, 0, 0, 0, 0, 0] = [5, 5, 0, 0, 10, 0, 0, 0, 0, 0] 인데 다른걸로 취급 중

def dfs(x,s) : 
    global cnt
    if s>t:
        return
    if x==bbb:
        if s==t:
            print(ch)
        return
    else :
        ch[x]=0
        dfs(x+1,s)
        ch[x]=m[x]
        dfs(x+1,s+m[x])
        
if __name__=='__main__' :
    p=[]
    m=[]
    bb=[]
    cnt=0
    t=int(input())
    k=int(input())
    for i in range(k) :
        a,b=map(int,input().split())
        bb.append(b)
        for _ in range(b):
            m.append(a)
    bbb=sum(bb)
    ch=[0]*(bbb)
    dfs(0,0)
    

==> 설명 상태트리를 듣고 구현한 내 풀이

def dfs(x,s) : 
    global cnt
    if s>t:
        return
    if x==k:
        if s==t:
            cnt+=1
        return
    else :
        for i in range(num[x]+1):
            dfs(x+1,s+(tp[x]*i))

if __name__=='__main__' :
    cnt=0
    tp=[]
    num=[]
    t=int(input())
    k=int(input())
    for i in range(k):
        a, b=(map(int, input().split()))
        tp.append(a)
        num.append(b)
    dfs(0,0)
    print(cnt)

<풀이>

import sys
sys.stdin=open("input.txt", "r")
def DFS(L, sum):
    global cnt
    if sum>m:
        return
    if L==n:
        if sum==m:
            cnt+=1
    else:
        for i in range(cn[L]+1):
            DFS(L+1, sum+(cv[L]*i))

m=int(input())
n=int(input())
cv=list()
cn=list()
for i in range(n):
    a, b=map(int, input().split())
    cv.append(a)
    cn.append(b)
cnt=0
DFS(0, 0)
print(cnt)

<반성점>

• 상태트리를 구현할 때 부분집합 상태트리, 조합 상태트리 같은 걸로만 풀려고 사고를 확장하지 못했다
• 너무 부분집합으로만 해결하려고 무식하게 붙잡고 있던 것 같다
  기존에 배운 거 말고도 유연하게 사고를 장착하자.. i기준으로 돌리는 것이라던가

<배운 점>

• 새로운 유형의 상태트리!

<2차 내 풀이>

=> 정답은 나오지만 시간초과

def dfs(x,s) :
    global cnt
    if x>k:
        return
    if x==k :
        if s==m:
            cnt+=1
    else :
        for i in range(nn[x]+1) :
            dfs(x+1, s+(i*pp[x]))
if __name__=='__main__' :
    cnt=0
    pp=[]
    nn=[]
    m=int(input())
    k=int(input())
    for i in range(k) :
        a,b=map(int,input().split())
        pp.append(a)
        nn.append(b)
    dfs(0,0)
print(cnt)

=> def dfs(x,s) :
global cnt
if x>k or s>m: , 이 조건까지 추가해주니깐 시간 훨씬 단축