파이썬 알고리즘 082 | 위상정렬(그래프 정렬)

82. 위상정렬(그래프 정렬)

위상정렬은 어떤 일을 하는 순서를 찾는 알고리즘입니다.
각각의 일의 선후관계가 복잡하게 얽혀있을 때 각각 일의 선후관계를 유지하면서 전체 일의
순서를 짜는 알고리즘입니다.
만약 아래와 같은 일의 순서를 각각 지키면서 전체 일의 순서를 정한다면
1 4 //1번일을 하고 난 후 4번일을 해야한다.
5 4
4 3
2 5
2 3
6 2

전체 일의 순서는 1, 6, 2, 5, 4, 3과 같이 정할 수 있다. 전체 일의 순서는 여러 가지가 있습
니다 그 중에 하나입니다.
▣ 입력설명
첫 번째 줄에 전체 일의 개수 N과 일의 순서 정보의 개수 M이 주어집니다.
두 번째 줄부터 M개의 정보가 주어집니다.
▣ 출력설명
전체 일의 순서를 출력합니다.
▣ 입력예제 1
6 6
1 4
5 4
4 3
2 5
2 3
6 2
▣ 출력예제 1
1 6 2 5 4 3

<내 풀이>

접근방법을 알지 못함

<풀이>

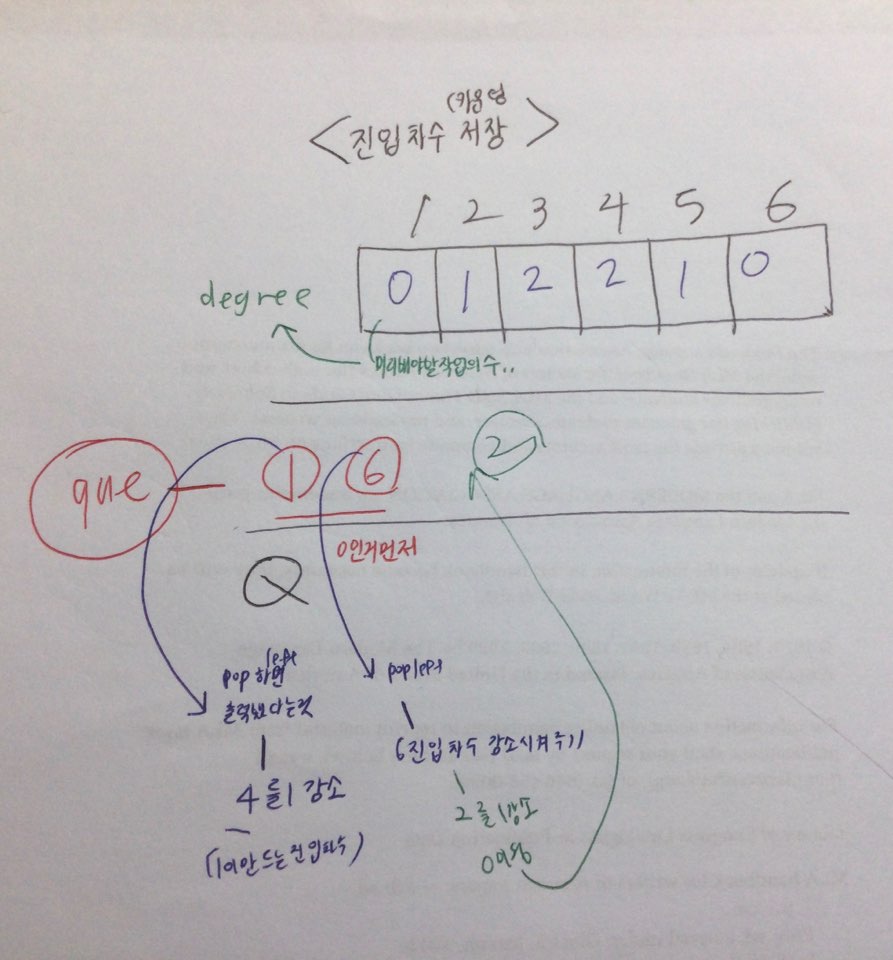
• 진입차수의 갯수 : 사전에 선행해서 수행되어야 할 임무
• 진입차수 입력해주는 값 만들고 유연하게 넣어줬다가 빼주면서
  그에 상응하는 동작 하기 (degree에서 값 빼주는 동작)

import sys
from collections import deque
sys.stdin=open("input.txt", "r")
n, m=map(int, input().split())
graph=[[0]*(n+1) for _ in range(n+1)]
degree=[0]*(n+1)
dQ=deque()
for i in range(m):
    a, b=map(int, input().split())
    graph[a][b]=1
    degree[b]+=1 #진입차수 수를 갱신해주는 것
for i in range(1, n+1):
    if degree[i]==0: #차수가 0이라서 선행해야 할 작업이 없는 애는 바로 q에 넣어버리면 됨
        dQ.append(i)
while dQ:
    x=dQ.popleft()
    print(x, end=' ')
    for i in range(1, n+1):
        if graph[x][i]==1: #얘가 진입차수 였던 애들한테서 진입차수의 갯수 하나씩 빼주기
            degree[i]-=1
            if degree[i]==0: #진입차수가 0이 되면 앞에서 더이상 처리해줄 값이 없으니깐 q에 넣어주기
                dQ.append(i)
                

<반성점>

<배운 점>

• 위상 정렬에서는 진입 차수가 중요하다 (나에게 들어오는 방향의 갯수)

• 진입 차수를 각 노드 마다 입력해줘야 한다 *

• 큐 활용해주기

  <2차 내 풀이>

 
n,m=map(int,input().split())
dy=[0]*(n+1)
for i in range(m) :
    a,b=map(int,input().split())
    dy[b]+=1
print(dy)

=> 진입 차수 카운팅 해주는 것까지만 기억남 ㅠㅠ

=> 인강 듣고 풀이 :

from collections import deque
n,m=map(int,input().split())
g=[[0]*(n+1) for _ in range(n+1)]
degree=[0]*(n+1)
q=deque()
p=[]

for i in range(m) :
    a,b=map(int,input().split())
    g[a][b]=1
    degree[b]+=1
for i in range(1,n+1) : 
    if degree[i]==0:
        q.append(i)
while q:
    k=q.popleft()
    p.append(k)
    for i in range(1,n+1) :
            if g[k][i]==1 :
                degree[i]-=1
                if degree[i]==0:
                    q.append(i)
print(p)