108. 골드바흐의 추측
1보다 큰 자연수 중에서 1과 자기 자신을 제외한 약수가 없는 자연수를 소수라고 한다. 예를 들어, 5는 1과 5를 제외한 약수가 없기 때문에 소수이다. 하지만, 6은 6 = 2 × 3 이기 때문에 소수가 아니다.
골드바흐의 추측은 유명한 정수론의 미해결 문제로, 2보다 큰 모든 짝수는 두 소수의 합으로 나타낼 수 있다는 것이다. 이러한 수를 골드바흐 수라고 한다. 또, 짝수를 두 소수의 합으로 나타내는 표현을 그 수의 골드바흐 파티션이라고 한다. 예를 들면, 4 = 2 + 2, 6 = 3 + 3, 8 = 3 + 5, 10 = 5 + 5, 12 = 5 + 7, 14 = 3 + 11, 14 = 7 + 7이다. 10000보다 작거나 같은 모든 짝수 n에 대한 골드바흐 파티션은 존재한다.
2보다 큰 짝수 n이 주어졌을 때, n의 골드바흐 파티션을 출력하는 프로그램을 작성하시오. 만약 가능한 n의 골드바흐 파티션이 여러 가지인 경우에는 두 소수의 차이가 가장 작은 것을 출력한다.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고 짝수 n이 주어진다.
출력
각 테스트 케이스에 대해서 주어진 n의 골드바흐 파티션을 출력한다. 출력하는 소수는 작은 것부터 먼저 출력하며, 공백으로 구분한다.
제한
4 ≤ n ≤ 10,000
예제 입력 1
3
8
10
16
예제 출력 1
3 5
5 5
5 11
1) 어떤 전략(알고리즘)으로 해결?
- 에라스토테네스
- 미리 maxnum 기준으로 소수들 구해놓기
- 그 다음에 입력값들 각각 경우 판별
=> 이때 만약 가능한 n의 골드바흐 파티션이 여러 가지인 경우에는 두 소수의 차이가 가장 작은 것을 출력한다 라는 조건이 있으므로 2부터~입력값 사이에 있는 소수들 중 가운데 있는 아이들을 찾아야 됨
1) 만약 소수의 갯수가 홀수개 -> 가운데 있는 아이
2) 만약 소수의 갯수가 짝수개 -> 나누기 2 하면 두개가 센터에 있을텐데 이 두개가 ㅇㅇ
2) 코딩 설명
<내 풀이>
import time
t=int(input())
inputs=[0]*t #입력값들 담는 배열
sosu=[0]*10000
index=0
for i in range(t) : #입력값들 받아주는 중
n=int(input())
inputs[index] =n
index+=1
maxinput = max(inputs) #입력값들 중에서 가장 큰 값 찾기
sosu[1]=1
for i in range(2,maxinput) :
if sosu[i]==0:
for j in range(i*2,maxinput,i) :
sosu[j]=1 #소수 아닌 것들은 체크
#sosu는 1부터 max 입력값까지의 인덱스를 가진아이
#start = time.time()
for i in range(t) :
for j in range(inputs[i]//2,1,-1) :
if sosu[j]==0 and sosu[inputs[i]-j]==0 :
print(j,inputs[i]-j)
break
#print("time :", time.time() - start) # 현재시각 - 시작시간 = 실행 시간
=> 우선 sosu 를 구해놓으면 sosu 아이를 잘 이용하도록 하자
=> sosu 배열의 인덱스만 잘 활용한다면 문제 clear
<내 틀린 풀이, 문제점 고쳐나가기 과정....>
t=int(input())
inputs=[0]*t #입력값들 담는 배열
sosu=[0]*10000
index=0
for i in range(t) : #입력값들 받아주는 중
n=int(input())
inputs[index] =n
index+=1
maxinput = max(inputs) #입력값들 중에서 가장 큰 값 찾기
sosu[1]=1
for i in range(2,maxinput) :
if sosu[i]==0:
for j in range(i*2,maxinput,i) :
sosu[j]=1 #소수 아닌 것들은 체크
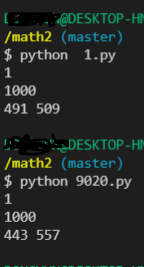
for i in range(t) :
index2=0
cntsosu=0 #입력값들마다 가지는 소수의 갯수다르므로 초기화 꼭!~
tempsosu=[0]*(inputs[i])
for j in range(2,inputs[i]) : #2부터 i번째 입력값 사이에 있는 소수 담기 작업
if(sosu[j]==0) :
cntsosu+=1 #소수의 갯수 , 여기서중간값 구해야 돼가지고
tempsosu[index2]=j #여기에 각 입력값까지의 소수들 담김
index2+=1
chk=0
print(tempsosu)
print(cntsosu)
print(cntsosu//2-1)
print(tempsosu[cntsosu//2-1])
if cntsosu%2==0 : #짝수라면 중간-1, 중간+1 두개 출력
while chk==0 and cntsosu<2*inputs[i]:
if inputs[i]-tempsosu[cntsosu//2-1] in tempsosu :
chk=1
a=inputs[i]-tempsosu[cntsosu//2-1]
b=tempsosu[cntsosu//2-1]
print("ab:",a,b)
else :
cntsosu+=2
else :
while chk==0 and cntsosu<2*inputs[i]:
if inputs[i]-tempsosu[cntsosu//2] in tempsosu :
chk=1
a=inputs[i]-tempsosu[cntsosu//2]
b=tempsosu[cntsosu//2]
print(a,b)
else :
cntsosu+=2
if a<b:
print(a,b)
else :
print(b,a)
=> 이렇게 하면 최소차이를 나타내는 아이를 찾을 수 없음
==> 따라서 여기에다가 끝까지 돌면서 min 이라는 차이 값이 최소인 애를 판별하는 변수를 넣어서
min을 비교하면서 최소 값을 가지는 두 수를 찾기로 결정
==> 아래의 코드로 구현
t=int(input())
inputs=[0]*t #입력값들 담는 배열
sosu=[0]*10000
index=0
for i in range(t) : #입력값들 받아주는 중
n=int(input())
inputs[index] =n
index+=1
maxinput = max(inputs) #입력값들 중에서 가장 큰 값 찾기
sosu[1]=1
for i in range(2,maxinput) :
if sosu[i]==0:
for j in range(i*2,maxinput,i) :
sosu[j]=1 #소수 아닌 것들은 체크
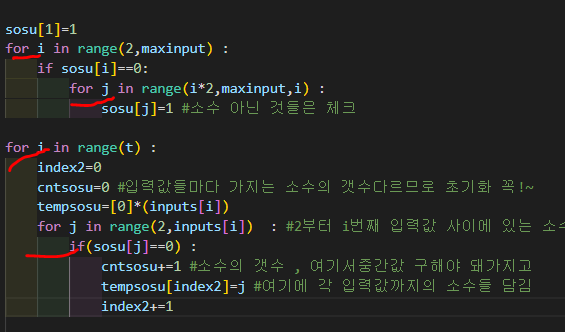
for i in range(t) :
index2=0
cntsosu=0 #입력값들마다 가지는 소수의 갯수다르므로 초기화 꼭!~
tempsosu=[0]*(inputs[i])
for j in range(2,inputs[i]) : #2부터 i번째 입력값 사이에 있는 소수 담기 작업
if(sosu[j]==0) :
cntsosu+=1 #소수의 갯수 , 여기서중간값 구해야 돼가지고
tempsosu[index2]=j #여기에 각 입력값까지의 소수들 담김
index2+=1
minvalue = inputs[i]+2
if cntsosu%2==0 : #짝수라면 중간-1, 중간+1 두개 출력
while cntsosu<2*inputs[i]:
if inputs[i]-tempsosu[cntsosu//2-1] in tempsosu :
if minvalue > abs((inputs[i]-tempsosu[cntsosu//2-1])-tempsosu[cntsosu//2-1]):
minvalue= abs(tempsosu[cntsosu//2-1]-(inputs[i]-tempsosu[cntsosu//2-1]))
a=inputs[i]-tempsosu[cntsosu//2-1]
b=tempsosu[cntsosu//2-1]
cntsosu+=2
else :
while cntsosu<2*inputs[i]:
if inputs[i]-tempsosu[cntsosu//2] in tempsosu :
if minvalue > abs((inputs[i]-tempsosu[cntsosu//2])-tempsosu[cntsosu//2]):
minvalue = abs((inputs[i]-tempsosu[cntsosu//2])-tempsosu[cntsosu//2])
a=inputs[i]-tempsosu[cntsosu//2]
b=tempsosu[cntsosu//2]
cntsosu+=2
if a<b:
print(a,b)
else :
print(b,a)
=> 답은 맞는데 시간초과가 걸린다.. 그럴만하지.. ㅡminvalue 찾느라 삥삥 돌아야 하니..
=> 시간 초과되는 부분을 어디에서 줄일 수 있을까!?
이 이중 for문도참 오래 걸릴 듯...
for i in range(t) : #소수를 따로 담아주는 리스트
index2=0
cntsosu=0 #입력값들마다 가지는 소수의 갯수다르므로 초기화 꼭!~
tempsosu=[0]*(inputs[i])
for j in range(2,inputs[i]) : #2부터 i번째 입력값 사이에 있는 소수 담기 작업
if(sosu[j]==0) :
cntsosu+=1 #소수의 갯수 , 여기서중간값 구해야 돼가지고
tempsosu[index2]=j #여기에 각 입력값까지의 소수들 담김
index2+=1
minvalue = inputs[i]+2
#소수 담은 리스트를
if cntsosu%2==0 : #짝수라면 중간-1, 중간+1 두개 출력
while cntsosu<2*inputs[i]:
if inputs[i]-tempsosu[cntsosu//2-1] in tempsosu :
if minvalue > abs((inputs[i]-tempsosu[cntsosu//2-1])-tempsosu[cntsosu//2-1]):
minvalue= abs(tempsosu[cntsosu//2-1]-(inputs[i]-tempsosu[cntsosu//2-1]))
a=inputs[i]-tempsosu[cntsosu//2-1]
b=tempsosu[cntsosu//2-1]
cntsosu+=2
else :
while cntsosu<2*inputs[i]:
if inputs[i]-tempsosu[cntsosu//2] in tempsosu :
if minvalue > abs((inputs[i]-tempsosu[cntsosu//2])-tempsosu[cntsosu//2]):
minvalue = abs((inputs[i]-tempsosu[cntsosu//2])-tempsosu[cntsosu//2])
a=inputs[i]-tempsosu[cntsosu//2]
b=tempsosu[cntsosu//2]
cntsosu+=2
if a<b:
print(a,b)
else :
print(b,a)=> 이 부분에서 맨 처음에 각 input의 소수담는 통을 따로따로 만드느라 오래걸려뜸.. 따라서 일단 소수 한번에 받아버리고,이 소수 카운트만 갱신하면 안될까?
<개선포인트들>
1) 골드바흐 파티션의 수들은 주어진 수의 1/2 보다 항상 작음
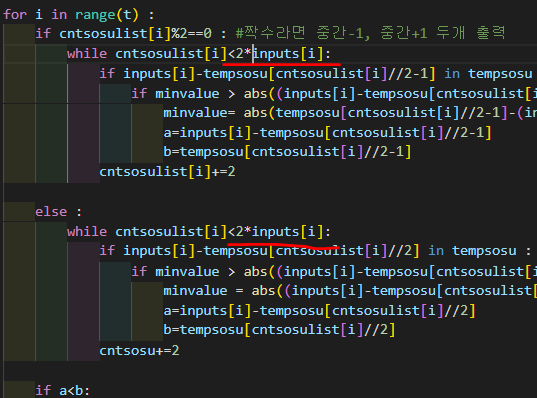
따라서 원래는 cntsosulist에 담긴 각 소수의 갯수들을 갱신할 때 (cntsosulist 에 담긴 수들을 사용할 때 항상 중간값 기준으로 실행하느라 나누기2를 하고 있었기 때문에) +2를 해주는데, 그 한계값을 입력값의 두배로 했었다, 근데 사실상 끝까지 갈 필요도 없고 해당값의 나누기 2만큼보다 작은 수가 최댓값이기 때문에 저 곱하기 2해준 부분을 제외시켜도 문제가 없다.
- 따라서 아래와 같이 inputs[i]에 갈 때까지만으로 수정했음
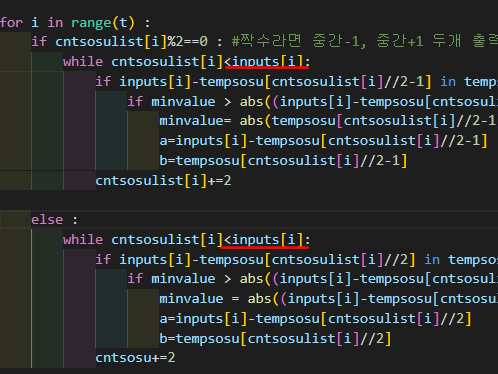
=> 기존 코드로 걸리던 시간

=> 개선 후 코드로 걸린 시간 , 무려 절반이나 덜 걸리게 된다
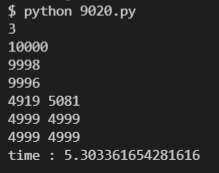
==> but 여전히 2초의 두배를 훌쩍 넘는 긴 시간이 걸린다.
==> time을 옮겨가면서 재보니 당연하게도 minvalue 측정하는 부분에서 너무 많이 걸림.
==> 최적의 방법이 있을까?
<반성 점>
-> 시간 복잡도를 잘 고려하자
-> 최대한 리팩토링 할 수 있는 만큼 하자
-> 입력 받는 위치를 식 안에 해도 된다
<배운 점>
-> 생각을 충분히 하고 문제를 푼다면 몸이 덜 고생할 것. . . . .

