파이썬 알고리즘 182번 | [백준 1463번] 1로 만들기 - DP

Yunny.Log ·2022년 6월 22일

Algorithm

목록 보기

185/318

182. 1로 만들기

1) 어떤 전략(알고리즘)으로 해결?

2) 코딩 설명

주석 설명

2023-01-24-스스로 다시 푼 풀이

import sys

n = int(sys.stdin.readline().rstrip())
dp = [int(1e9) for _ in range(n+1)]
cnt = 0 # 연산 횟수

# 1) X가 3으로 나누어 떨어지면, 3으로 나눈다. 
#       => 3으로 곱한다고 생각
# 2) X가 2로 나누어 떨어지면, 2로 나눈다. 
#       => 2를 곱한다고 생각
# 3) 1을 뺀다. 
#       => 1을 더한다고 생각 
# 정수 N이 주어졌을 때, 위와 같은 연산 세 개를 적절히 사용해서 
# 1을 만들려고 한다. 연산을 사용하는 횟수의 최솟값을 출력하시오.

# N에서 1을 만드는 것 -> 1에서 N을 만드는 것으로 생각하기 ! 

dp[1] = 0

for i in range(1,n+1) : 
    if i*2 <= n : 
        dp[i*2] = min(dp[i*2], dp[i]+1)
    if i*3 <= n : 
        dp[i*3] = min(dp[i*3], dp[i]+1)
    if i+1 <=n : 
        dp[i+1] = min(dp[i+1], dp[i]+1)

print(dp[n])

2022-06-22 풀이(다른 분의 코드를 본 후 풀이만 적은 것)

코드 및 설명 출처 : https://hongcoding.tistory.com/46

n = int(input())

dp = [0] * (n+1) # 0 으로 처음에 초기화해준다. 

for i in range(2, n+1): 
# 2부터 도는 이유는 1이 되면 계산할 겨를 X , 어차피 1이니깐 연산 멈춤

# 덮어씌워즬 우선 순위 
# (1) 1빼는 과정(직전 아이 +1) => 카운트 많이 필요
# (2) 2 나누는 과정 (1) 보다는 카운트 덜 필요 (2) 보다는 많이 필요
# (3) 3 나누는게 제일 빠르니 얘를 마지막에 

    dp[i] = dp[i-1] + 1 # 자기 직전의 아이의 카운트에 1을 더한 수를 자신으로 

    if i % 2 == 0: 

# 자기 이전 아이 (빼기 1) + 지금연산(1) VS 나를 2로 나눈 수가 2배한 아이의 카운트 + 지금연산(1)
        dp[i] = min(dp[i], dp[i//2]+1)

# 자기 이전 아이 (빼기 1 OR 2로나눈 아이 카운트 ) + 지금연산(1) VS 
# 나를 2로 나눈 수가 2배한 아이의 카운트 + 지금연산(1)
    if i % 3 == 0:
        dp[i] = min(dp[i], dp[i//3] + 1)

print(dp[n])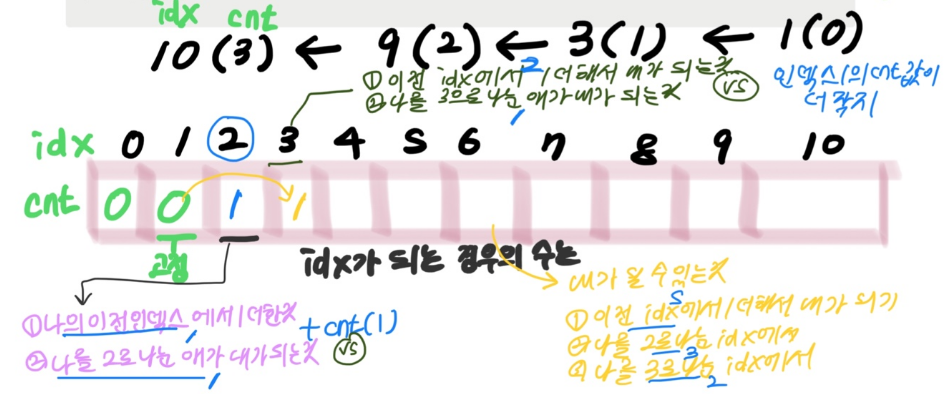

n = int(input())

dp = [0] * (n+1) # 0 으로 처음에 초기화해준다. 

for i in range(2, n+1): 
# 2부터 도는 이유는 1이 되면 계산할 겨를 X , 어차피 1이니깐 연산 멈춤

    if i % 2 == 0: #2로 나눠지면 자기 자신(1 더했던 것)
        dp[i] = min(dp[i-1] + 1, dp[i//2]+1) # 1은 언제나 뺄 수 있어서 
    if i % 3 == 0:
        dp[i] = min(dp[i-1] + 1, dp[i//3] + 1)

print(dp[n])

<내 틀렸던 풀이, 문제점>

시간 제한이 있는 걸 봤음에도 한번 시도해본 재귀로 모든 경우의 수 다 탐색해보는 풀이 ㅎㅎ


import sys

n= int(sys.stdin.readline().rstrip())
cnt=0
lis =[]
def recur(n, cnt) :
    global lis
    if n==1 :
        lis.append(cnt)
        return
    else : 
        nn1 = n
        nn2 = n
        nn3 = n
        cnt+=1

        if (n-1)%2==0 or (n-1)%3==0 or (n-1)==1 :
            nn3-=1
            recur(nn3, cnt)

        if n%2==0 : 
            nn1//=2
            recur(nn1, cnt)
        if n%3==0 : 
            nn2//=3
            recur(nn2, cnt)
        
recur(n, cnt)

print(min(lis))