241. 최단경로
1) 어떤 전략(알고리즘)으로 해결?
다익스트라
2) 코딩 설명
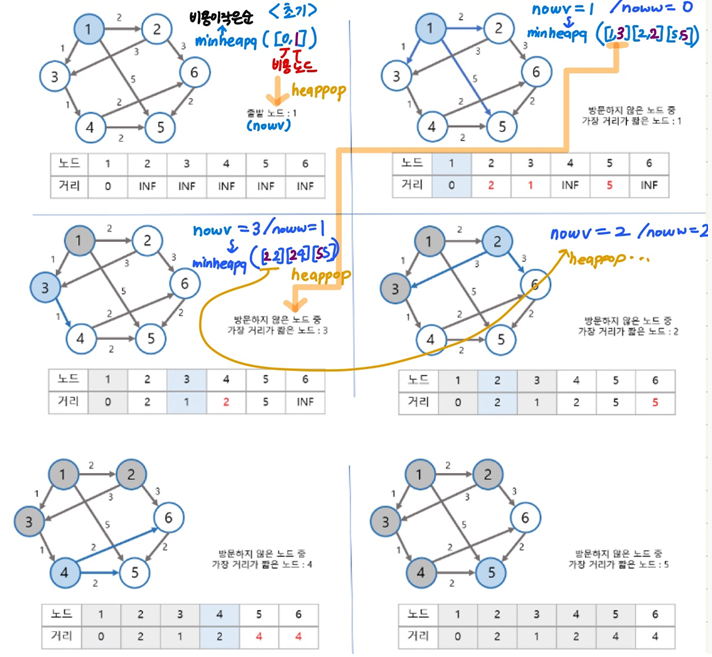
<내 풀이>
import heapq
import sys
V,E = map(int , sys.stdin.readline().rstrip().split())
start = int(sys.stdin.readline())
graph = [ [] for _ in range(V+1)]
answer = [int(1e9)for _ in range(V+1)]
for i in range(E) :
u,v,w = map(int , sys.stdin.readline().rstrip().split())
graph[u].append((v,w))
def dijkstra(start):
minheapq=[]
heapq.heappush(minheapq, (0,start))
# w,v - 시작점으로부터 시작점 w : 0 / 시작점 노드부터 시작
answer[start] = 0
while minheapq: # 가장 w가 작은 노드부터 검사 (bfs 와 비슷 흐름)
noww, nowv = heapq.heappop(minheapq)
if answer[nowv] < noww :
# nowv의 최단거리라고 기록돼있는 것이 noww 보다 작으면 더 이상 작아질 수 없다
# (왜냐면 이제부터는 noww+알파 로 최단경로 기록되니깐)
# nowv 보다 작다는 것은 이미 이 노드는 heappop 됐었다는 증거
# (처음에 heappop 될 수록 nowc가 가장 작은 상태)
# => 이는 방문 완료, 이미 확정됐다는 증거
# 한번 방문할 때 최단 경로가 이미 기록되어있다는 뜻이므로 방문 했을 시엔 검사할 필요 x
continue
for i in graph[nowv]: # 방문 안 한 노드라면 인접 노드 체크 필요
cmpv, cmpw = i[0], i[1] # 그래프에 (v,w) 로 담았었음
tmpcost = noww + cmpw # 현재 answer[cmpv] 에 기록된 최단경로와 비교해볼 대상
if tmpcost < answer[cmpv]: # 현재 answer[cmpv] 에 기록된 최단경로보다 더 짧은 경로라면
answer[cmpv] = tmpcost # answer[cmpv] 를 비교대상으로 대체
heapq.heappush( minheapq, ( tmpcost, cmpv ) ) #
dijkstra(start)
for i in range(1,V+1) :
if answer[i]<1e9 :
print(answer[i])
else : print("INF")
<내 틀렸던 풀이, 문제점>
메모리초과
import sys
from collections import deque
#####################################################################
v,e = map(int, sys.stdin.readline().rstrip().split())
start = int(sys.stdin.readline().rstrip())
mapp = list([0 for _ in range(v+1)] for _ in range(v+1))
#####################################################################
for i in range(e) :
uu,vv,ww = map(int, sys.stdin.readline().rstrip().split())
if mapp[uu][vv] :
if mapp[uu][vv] > ww :
mapp[uu][vv] = ww
else :
mapp[uu][vv] = ww
#####################################################################
# 검사할 큐 / 타겟 노드 / 길이 갱신 / 방문 처리
def bfs(deq, target_node, visit) :
global minim
global possible
while deq :
now, now_weight = deq.popleft()
if now == target_node :
# print(now, "|||", minim, length)
possible = True # 한번이라도 타켓 도달하면 가능 , INF 아님
if now_weight < minim :
minim = now_weight
return minim
for m in range(1,v+1) : # m[0] 은 weight, m[1] 은 v, 간선
# print(now, mapp[now][m])
# mapp[now][m] = 가중치 now->m 갈때
# m이 간선이다.
if mapp[now][m]!=0 and visit[m] != 1 : # 방문안했을 때
visit[m] = 1
deq.append((m, now_weight+mapp[now][m]))
# bfs(deq, target_node, length+m[0], visit)
# visit[mapp[now][m]] = 0
######################################################################
for i in range(v) :
#print(i, "번 째지이이이이")
if start == i+1 : # 시작점 자신은 0으로 출력
print(0)
else : # 경로가 존재하지 않는 경우에는 INF를 출력
q = deque()
q.append((start, 0))
visit = [0 for _ in range(v+1)]
minim = 1000000001
possible = False
res = bfs(q, i+1, visit)
#print(possible)
if possible : # 한번이라도 POSSIBLE = TRUE
# 였다면 경우의 수 존재
#print("hiiiiiiii")
print(res)
else :
#print("h9oojo")
print("INF")
<반성 점>
<배운 점>
- 다익스트라 개념 - 우선수위큐 (가중치 기준), BFS
- 플로이드와 다익스트라의 비교 - https://loosie.tistory.com/146

- 다익스트라
- 다익스트라 알고리즘은 우선순위 큐 + BFS의 형태를 가지고 있다.
- 각 정점까지의 최단 거리를 저장하는 배열 dp[]를 유지하며, 정점을 방문할 때마다 인접한 정점을 모두 검사한다.
- 간선 (u, v)를 검사한다고하면 u까지의 최단 거리에 (u, v)의 가중치를 더해 v까지의 경로의 길이를 찾는다.
- 만약 이 길이가 최단거리라면 dp[v]를 갱신하고, (v, dp[v])를 큐에 넣는다.
- 플로이드
- 다익스트라나 벨만포드는 한 시작점에서 다른 모든 정점까지의 거리를 구해준다.
- 모든 쌍 간의 최단 거리를 구하고 싶다면 플로이드 와샬 알고리즘을 사용하면 된다.

