파이썬 알고리즘 294번 | [백준 11780번] 플로이드 2 - 플로이드 워셜, 다익스트라 & 경로 추적

Yunny.Log ·2023년 1월 22일

Algorithm

목록 보기

298/318

294. 플로이드 2

1) 어떤 전략(알고리즘)으로 해결?

플로이드 워셜, 다익스트라 알고리즘
최소 비용으로 경로 구하는 것

2) 코딩 설명

2-1 ) 플로이드 워셜

플로이드 워셜은 DP 방식
dp 의 초기값을 무한대 (가장 큰 값) 로 설정해줍니다.
이후 3중 FOR문을 통해서 dp로 지금 dp 에 저장된 경로를 갱신시켜주는 방식입니다.
- 주의해야 할 점은 거쳐가는 부분이 가장 첫번째 for 문으로 와야한다는 점입니다.


for k in range(1,n+1) : # 이게 먼저 ! 
    for i in range(1,n+1) : 
        for j in range(1,n+1) :
            dp[i][j] = dp[i][k] + dp[k][j]

근데 이 문제에서 특이한 점은 그 최소 경로를 추적해야 한다는 것이었습니다.
이는 재귀함수를 통해서 경로를 추적할 수 있다고 합니다.
i에서 j로 갈때 거쳐가야 하는 k 가 갱신될 때마다 klist[i][j] = k 로 k를 기록해줘야 합니다.
그리고 위에서 dp와 klist 를 다 채우고나면 , 이제 경로도 출력해줘야 한다.

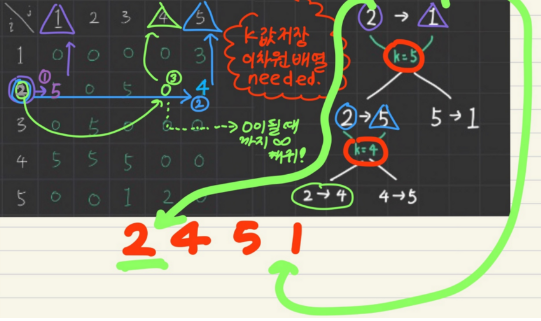
(위 검정색 이미지 출처 : https://hooongs.tistory.com/325)
이때 i에서 j로 가는 경로를 출력하면

시작점(i) - < 거쳐간 k 들 > - 끝 점(j)

로 출력이 될 것, 이때 거쳐간 k들은 계속 재귀함수를 돌면서 출력해주면 됩니다.
이때 재귀함수의 종료 조건은 find_path(i,j) 로 들어온 i,j 사이에 거치는 k가 없을 때입니다. 이때는 거치는 k가 없다는 뜻이므로 빈 리스트를 돌려주면 됩니다.
만약 0이 아니라면 k가 존재한다는 뜻이므로, k를 klis[i][j] 로 설정 후 , 이 i~k , k , k~j 를 거쳐가는 경로를 거치는 것이 확실시 되었으므로 이를 반환 값으로 설정해줍니다. 다만 i~k 와 k~j 사이에는 또 거치는 k가 존재할 수도 있으니 이 두개는 다시 한번 재귀함수를 호출해줍니다.
```
# 최소 비용 경로를 구하는 재귀함수
def find_path(i, j):
   if klis[i][j] == 0: # 끝
       return []
   k = klis[i][j] # 거치는 것 사이에 또 존재
   return find_path(i, k) + [k] + find_path(k, j)
```

그 다음, 도시 i에서 도시 j로 가는 경로를

for i in range(1, n+1):
for j in range(1, n+1):

    # 갈 수 없는 길이면 경로 no
    if dp[i][j] == 1e9 or dp[i][j] == 0 : 
        print(0)
        continue
    path = [i] + find_path(i, j) + [j] 
    # 경로 수 & 경로를 공백으로 구분해 출력
    print(len(path), end=' ' ) # 경로 수
    print(*path) # 경로

 
### 2-2 다익스트라 
- 시작하는 아이의 비용을 일단 0으로 설정 
- 출발 아이로부터 주변 노드들 검사하면서, 어떤 주변 노드로 갔을 때 제일 작을 지 체크하고 , 최소비용 갱신하고, heap에다가 넣어주는 방식 

<**기본 다익스트라**>
```python
def dijkstra(start):
    q=[]
    heapq.heappush(q,(0,start))
    distance[start]=0

    while q:
        # 가장 최단거리가 짧은 노드에 대한 정보 꺼내기
        dist, now = heapq.heappop(q)
        # 현재 처리된적이 있는 노드라면 pass
        if distance[now]<dist:
            continue
        # 현재 노드와 연결된 다른 인접한 노드들을 확인
        for i in graph[now]:
            cost = dist + i[1]
            # 현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
            if cost < distance[i[0]]:
                distance[i[0]]=cost
                heapq.heappush(q,(cost,i[0]))

여기에 경로 추적을 더해주려면 갱신하는 과정에서
- 현재 노드를 거쳐 내 주변의 노드 중 하나의 노드로 갈 때(최소비용이 드는) , 이 경로에 대해 현재노드를 기록해주면 됩니다.
- 즉 현재노드 -> 주변노드 경로를 갈 때 , 이 경로에 대한 값을 현재노드를 기록해주면 되는 것이지요.
- 결과를 출력할 때는 현재 노드로부터 부모 노드를 계속 가면서, 부모 노드를 프린트해주면서 나아가다가 루트 노드를 만나면 그만 출력하게 하면 되는 것입니다.


def dijkstra(start):
    q=[]
    heapq.heappush(q,(0,start))
    distance[start][0]=0

    while q:
        # 가장 최단거리가 짧은 노드에 대한 정보 꺼내기
        dist, now = heapq.heappop(q)
        # 현재 처리된적이 있는 노드라면 pass
        if distance[now][0]<dist:
            continue
        # 현재 노드와 연결된 다른 인접한 노드들을 확인
        for i in graph[now]:
            cost = dist + i[1]
            # 현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
            if cost < distance[i[0]][0]:
                distance[i[0]][0]=cost # 최단거리 갱신
                distance[i[0]][1]=now  # 부모노드 저장
                heapq.heappush(q,(cost,i[0]))
                
dijkstra(start)

<내 풀이> - 플로이드 워셜 이용


import sys

n = int(sys.stdin.readline().rstrip())
m = int(sys.stdin.readline().rstrip())
dp = [ list(int(1e9) for _ in range(n+1)) for _ in range(n+1)]
klis = [ list( 0 for _ in range(n+1)) for _ in range(n+1)]

for i in range(n+1) :
    dp[i][i] = 0

for _ in range(m) : 
    a,b,c = map(int,sys.stdin.readline().rstrip().split())
    # dp[a][b] = c
    dp[a][b] = min(dp[a][b], c) # 똑같은 경로에 대한 비용 들어올 수 있음 **

for k in range(1,n+1) : 
    for i in range(1,n+1) :
        for j in range(1,n+1) :
            # dp[i][j] = min( dp[i][j]  , dp[i][k]+ dp[k][j]) - 기존 플로이드 워셜
            if dp[i][j] > dp[i][k]+ dp[k][j] : 
                dp[i][j] = dp[i][k]+ dp[k][j]
                klis[i][j] = k

#  도시의 개수 k를 출력한다. 

for d in range(1,n+1) :
    for e in range(1,n+1) :
        if(dp[d][e]==(1e9)) :
            print(0)
        else : 
            print(dp[d][e], end= " ")
    print()
    
# 최소 비용 경로를 구하는 재귀함수
def find_path(i, j):
    if klis[i][j] == 0: # 끝
        return []
    k = klis[i][j] # 거치는 것 사이에 또 존재
    return find_path(i, k) + [k] + find_path(k, j)

# 그 다음, 도시 i에서 도시 j로 가는 경로를 
for i in range(1, n+1):
    for j in range(1, n+1):
        # 갈 수 없는 길이면 경로 no
        if dp[i][j] == 1e9 or dp[i][j] == 0 : 
            print(0)
            continue
        path = [i] + find_path(i, j) + [j]
        # 경로 수 & 경로를 공백으로 구분해 출력
        print(len(path), end=' ' ) # 경로 수
        print(*path) # 경로