2025.04.10 ~ 04.11
Algorithm
탐색
순차 탐색(Linear Search)
- 리스트의 처음부터 끝까지 하나씩 비교하며 원하는 값을 찾음
- 반복문을 통해 요소를 순서대로 탐색하는 것을 의미
- for(초기값;조건식;증감식){} 구조로 사용
- O(n), 데이터가 많아질수록 느려짐
이진 탐색(Binary Search)
- 반복문 중간에 피벗(middle 값)을 두어서 절반씩 범위를 줄이며 탐색
- 반복문, 재귀로 구현 가능
- O(log n)
DFS(깊이 탐색)
BFS(너비 탐색)
-> Stack, Queue를 이용, 재귀호출도 연관
방문배열
- 탐색을 이미 완료한 노드를 또 방문하게 되면 불필요한 작업을 진행하게 된다.
- 방문배열이라는 비어있는 배열을 선언을 하고 방문했던 노드에 대한 정보를 저장해 놓는 배열을 선언한다.
- 보통 boolen 타입 배열로 들렸는지 안들렸는지 확인한다.
- 노드는 보통 1부터 시작하고 배열은 0부터 인덱스가 시작된다.
- 노드와 인덱스의 수를 맞추기 위해 노드의 수보다 하나 많게 배열을 설정하고 인덱스 0을 사용하지 않는다.
간선
- 노드와 노드 간의 연결선
- edge
- List<List< Integer>> / int[][] 형태로 그래프 표현
- 방향이 있는 경우, 방향이 없는 경우로 나누어진다.
- 방향 그래프, 무방향 그래프, 가중치 그래프
DFS(깊이 탐색), BFS(너비 탐색)을 사용하는 문제
- 그래프 전체를 탐색하거나 연결 요소 개수 구하기 : DFS > BFS
- 도달 가능 여부만 확인 (도착할 수 있는가?) : DFS > BFS
- 모든 경로 탐색 (모든 경우의 수) : DFS
- 가능한 모든 조합 : DFS
- 최단 거리 : BFS
- 단계적 상태 변화 (감염 확산, 물 퍼지기 등) : BFS
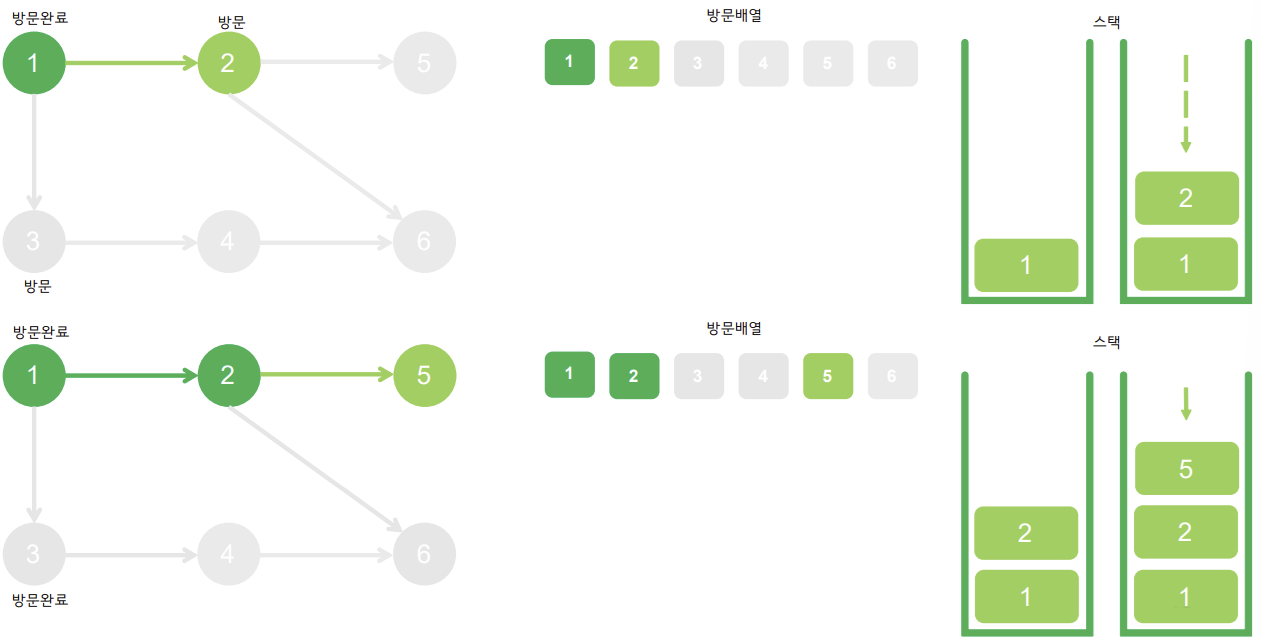
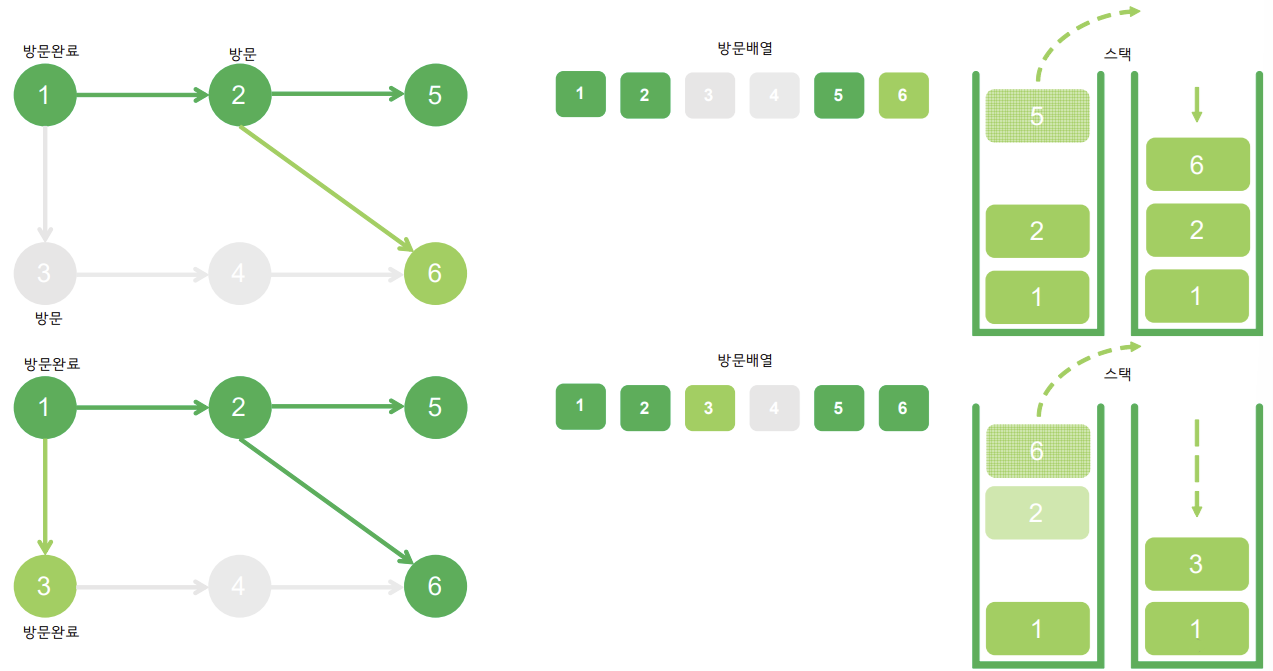
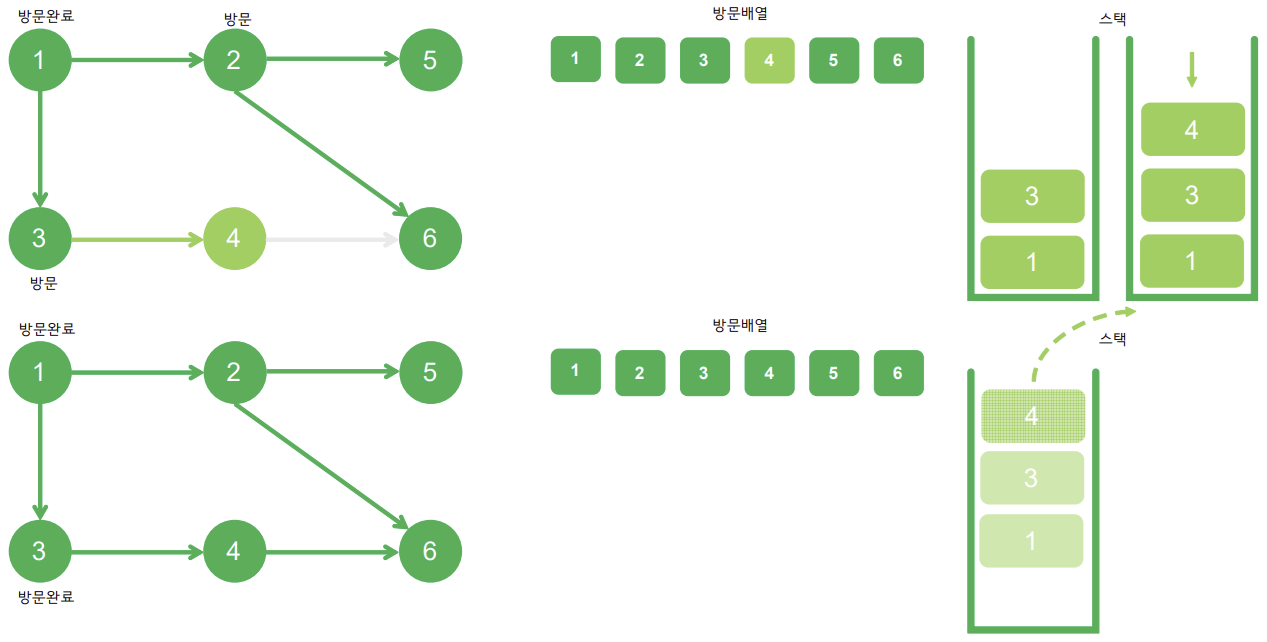
깊이 우선 탐색 DFS(Depth-First Search)
후입선출(LIFO : last in, first out) 구조인 stack, 재귀함수를 활용해 한쪽 분기를 정하여 최대 깊이까지 탐색을 맞친 후, 다른 쪽 분기로 이동하여 탐색을 수행하는 알고리즘
- 미로 탐색, 백트래킹 문제 등에서 활용
- 그래프 구조에서 모든 노드를 빠짐없이 탐색하는 데 유용

static int node, edge; <!-- 노드, 간선 -->
static int[][] map; <!-- 인접 행렬로 그래프를 나타내기 위함 -->
static boolean[] visit; <!-- 노드를 방문했을 때 TRUE를 넣어서 다시 방문하지 않도록 함 -->
<!-- 그래프의 간선 연결 정보를 이차원 배열로 표현 -->
map = new int[node + 1][node + 1]; <!-- 0번 인덱스 제외하고 사용 -->
<!-- 방문 배열 생성 (지나간 노드를 다시 방문하지 않기 위함) -->
visit = new boolean[node + 1];
<!-- 무방향 그래프 간선 연결 둘 다 1로 설정 -->
map[a][b] = map[b][a] = 1;- 재귀 함수로 DFS 알고리즘 구현 메소드
private static void dfsRecursive(int start) {
<!-- 해당 노드를 방문했으므로 방문 배열에 표기 -->
visit[start] = true;
<!-- start 노드의 이웃을 탐색하는 과정 -->
for(int i = 1; i <= node; i++) {
<!-- start 정점의 이웃 중 방문하지 않은 이웃을 찾는다. -->
if(map[start][i] == 1 && !visit[i]) {
<!-- 연결된 이웃 노드를 찾은 것이므로 count를 증가시키고
해당 이웃 노드를 방문해서 다시 이웃노드를 재귀적으로 탐색한다. -->
count++;
dfsRecursive(i);
}
}
}- stack으로 DFS 알고리즘 구현 메소드
private static void dfsStack(int start) {
Stack<Integer> stack = new Stack<>();
stack.push(start);
visit[start] = true;
while(!stack.isEmpty()) {
int current = stack.pop();
for(int i = 1; i <= node; i++) {
// 그래프의 노드가 있을 때 방문하지 않은 경우
if(map[current][i] == 1 && !visit[i]) {
stack.push(i);
visit[i] = true;
count++;
}
}
}
}재귀함수, stack 사용 시점
재귀함수 사용시점
- 노드 수가 적고 노드의 제한 개수가 정해져 있을 때
- 해당하는 노드가 간선으로 통해서 많은 그래프로 연결되어 있지 않을 때
- 방문 배열을 적절하게 사용하지 않을 때 무한 루프에 빠질 수 있다.
stack 사용 시점
- 노드의 제한 개수가 없을 때, 노드가 너무 많아 질 때
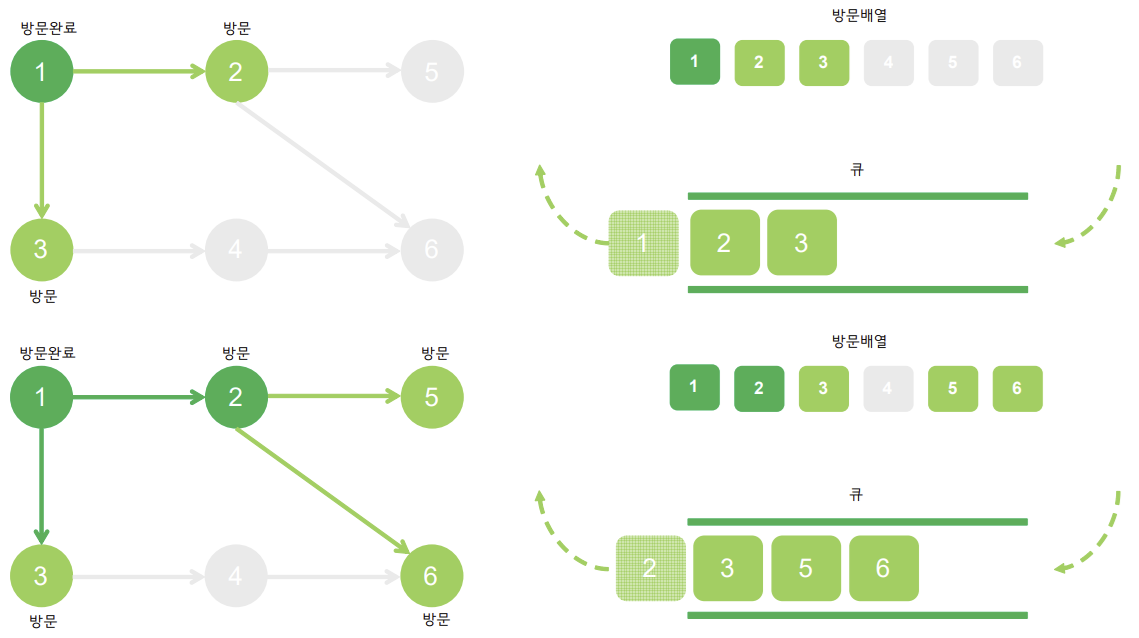
너비 우선 탐색 BFS(Breadth-First Search)
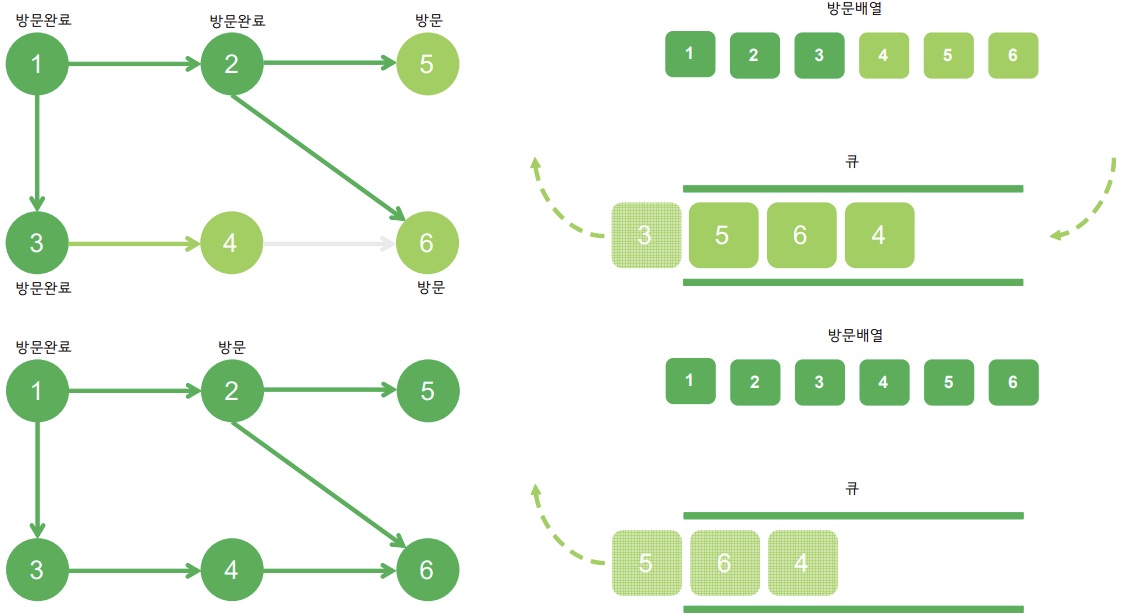
선입선출(FIFO : first in, first out) 구조인 queue를 활용해 탐색 시작 노드와 가까운 노드를 우선하여 탐색하는 알고리즘
- 격자형(2차원 좌표계)를 이용해 그래프의 범위를 체크하는 로직
- 4방향(상하좌우), 8방향으로 탐색
- 목표 노드에 도착하는 경로가 여러 개일 때 최단 경로를 보장
- 방문을 하면 시작 좌표(x, y)를 큐에 삽입하고 방문을 표시한다.
- 큐에서 꺼낸 좌표를 기준으로 4방향 탐색
- 배열 범위안, 방문하지 않은 경우, 유효한 값이라면 큐에 다시 넣고 방문처리(인접 노드 삽입)
- 이 과정을 반복해서 큐에 남아있는 노드가 없을때 까지 반복한다.
- 상하좌우 등 방향을 나타내는 경우 너비 우선 탐색을 사용하는 것이 유리함

static int M, N, K; <!-- 가로, 세로, 개수 -->
static int[][] map; <!-- 인접 행렬로 그래프를 나타내기 위함 -->
static boolean[] visit; <!-- 노드를 방문했을 때 TRUE를 넣어서 다시 방문하지 않도록 함 -->
<!-- 상하좌우, 같은 인덱스의 X,Y를 한 쌍으로 본다. -->
static int[] dirX = {0, 0, -1, 1}; // x축(열) 이동
static int[] dirY = {-1, 1, 0, 0}; // y축(행) 이동
<!-- x(열)와 y(행) 좌표를 가지는 Node 클래스 -->
<!-- 한 지점을 큐에 넣을 때, 그 지점의 한 쌍의 좌표를 함께 기억하기 위한 노드 -->
<!-- java는 좌표를 저장할 수 있는 node 클래스가 없기 때문에 따로 지정 -->
static class Node {
int x;
int y;
public Node(int x, int y) {
this.x = x;
this.y = y;
}
}
- 인덱스와 좌표를 맞추지 않는 경우
<!-- 현재 좌표 -->
static int cx, cy;
static Queue<Node> queue = new LinkedList<>();
<!-- 좌표 범위 확인 -->
static boolean rangeCheck() {
return cx >= 0 && cy >= 0 && cx < M && cy < N;
}
<!-- 행, 열의크기를 바꾸지 않는다 -->
map = new int[M][N];
visit = new boolean[M][N];
bfs(i, j);
static void bfs(int x, int y) {
<!-- 해당 좌표를 방문한 좌표에 삽입 -->
visit[x][y] = true;
<!-- 큐에 좌표 한 쌍으로 삽입 -->
queue.offer(new Node(x, y));
<!-- 큐의 저장해 놓았던 것을 꺼내와서 탐색을 한다. -->
while(!q.isEmpty()) {
Node node = q.poll();
<!-- 상하좌우 살펴보기 -->
for(int i = 0; i < 4; i++) {
cx = node.x + dirX[i];
cy = node.y + dirY[i];
<!-- 가장 모서리 혹은 끝에 있는 요소들은 상하좌우를 판단하려고 할 때
없는 공간을 참조할 수 있게 된다.
IndexOutOfBound Exception 이 발생하기 때문에
외부에 Error 방지용 메서드 선언 -->
<!-- 범위 확인 && 중복 방문 확인(아직 방문하지 않을 경우 실행)
&& 해당 좌표가 실제로 존재하는지 확인(존재하면 탐색 큐에 다시 넣고 탐색) -->
if(rangeCheck() && !visit[cx][cy] && map[cx][cy] == 1) {
queue.offer(new Node(cx, cy));
visit[cx][cy] = true;
}
}
}
}- 인덱스와 좌표를 맞추는 경우
<!-- 행, 열의크기를 바꾼다. -->
map = new int[N][M];
visit = new boolean[N][M];
bfs(j, i);
static void bfs(int x, int y) {
<!-- 해당 좌표를 방문한 좌표에 삽입 -->
visit[y][x] = true;
<!-- 큐에 좌표 한 쌍으로 삽입 -->
queue.offer(new Node(x, y));
<!-- 큐의 저장해 놓았던 것을 꺼내와서 탐색을 한다. -->
while(!queue.isEmpty()) {
Node node = queue.poll();
<!-- 상하좌우 살펴보기 -->
for(int i = 0; i < 4; i++) {
cx = node.x + dirX[i];
cy = node.y + dirY[i];
<!-- 범위 확인 && 중복 방문 확인(아직 방문하지 않을 경우 실행)
&& 해당 좌표가 실제로 존재하는지 확인(존재하면 탐색 큐에 다시 넣고 탐색) -->
if(rangeCheck() && !visit[cy][cx] && map[cy][cx] == 1) {
queue.offer(new Node(cx, cy));
visit[cy][cx] = true;
}
}
}
}최단거리(BFS)
먼저 방문한 노드를 기준으로 가장 가까운 노드부터 탐색
- 시작점에서 출발하여 거리 1 노드를 모두 방문한 후, 거리 2 노드를 방문하는 방식으로 진행
- 어떤 노드에 도달했을 때, 처음 도달한 순간이 곧 최단 거리
static int N, M;
static int[][] map;
static boolean[][] visit;
static int[] dirX = {0, 0, -1, 1};
static int[] dirY = {-1, 1, 0, 0};
static class Node {
int x;
int y;
public Node(int x, int y) {
this.x = x;
this.y = y;
}
}
static Queue<Node> queue = new LinkedList<>();
<!-- 출발 지점 -->
bfs(0, 0);
static void bfs(int x, int y) {
queue.add(new Node(x, y));
visit[x][y] = true;
<!-- 시작 지점에서부터 큐를 이용해서 큐에 담기는 노드가 제거 될 때까지 너비 우선 탐색을 진행 -->
while(!queue.isEmpty()) {
<!-- 현재 탐색을 진행할 노드 -->
Node node = queue.poll();
<!-- 해당 정점에서 상하좌우를 살펴보는 반복문 -->
for(int i = 0; i < 4; i++) {
int cx = node.x + dirX[i];
int cy = node.y + dirY[i];
<!-- 좌표가 전체 범위를 넘어간다면 확인이 불필요하므로 다음 방향 확인 -->
if(cx < 0 || cy < 0 || cx >= N || cy >= M) continue;
<!-- 방문 했던 좌표이거나 갈 수 없는 곳이라면 확인이 불필요하므로 다음 방향 확인 -->
if(visit[cx][cy] || map[cx][cy] == 0) continue;
<!-- 유효한 좌표이면 탐색 대상 큐에 추가 -->
<!-- 현재 좌표까지의 거리 +1을 저장 (이동 거리 누적) -->
queue.offer(new Node(cx, cy));
visit[cx][cy] = true;
map[cx][cy] = map[node.x][node.y] + 1;
}
}
}
좌표와 인덱스의 차이
좌표 f(x, y)
- x 증가 -> 오른쪽 이동
- y 증가 -> 위로 이동
인덱스[row][col]
- col 증가 -> 오른쪽 이동
- row 증가 -> 아래쪽 이동
좌표와 인덱스 차이를 신경써야되는 문제
- 회전연산 문제
- 색칠 문제
- 패턴 찾기 문제(오목, 퍼즐, 테트리스)
문자열을 나누는 방법
입력 받는 문자열이 공백 없이 한 줄로 붙어 있는 경우
- toCharArray()를 이용해 한 글자씩 분리
- Character.getNumericValue()를 이용해 정수로 변환
for(int i = 0; i < N; i++) {
<!-- .toCharArray() : 한 줄씩 읽어서 문자 배열로 변환 -->
char[] ch = br.readLine().toCharArray();
for(int j = 0; j < ch.length; j++) {
<!-- .getNumericValue() : 문자를 정수로 변환 -->
map[i][j] = Character.getNumericValue(ch[j]); // '1' -> 숫자 1
}
}문자로 된 노드를 정수 인덱스로 바꾸는 방법
아스키 코드 값을 이용해 알파벳에서 'A','a'을 빼준다.
- 뺀 값을 인덱스의 값으로 입력한다.
char parent = st.nextToken().charAt(0);
int idx = parent - 'A';
참고
그래프 탐색 문제는 노드 시작번호를 기준으로 코드를 작성하기 때문에 인덱스와 좌표를 맞춰주는 것이 좋다.
격자형(2차원 좌표계)는 인덱스 자체가 (x, y)좌표 역할을 한다. 좌표가 0부터 시작하므로 별도로 인덱스를 맞출 필요가 없다.
