2025.04.25 ~ 04.28
Algorithm
Dynamic programming (동적 계획법)
복잡한 문제를 여러 개의 간단한 문제로 분할하여 해결하고, 그 결과를 재사용함으로써 전체 문제의 해답을 효율적으로 구하는 방법
수행 방법
- 큰 문제를 작은 문제로 나눈다.
- 작은 문제들이 반복되어 나타나며 작은 문제들의 결과값은 항상 같다.(작은 문제들은 이미 최적의 값을가지고있다.)
- 각 작은 문제의 결과를 한 번만 계산하여 DP 테이블(배열 등)에 저장, 이후에는 저장된 결과를 재사용 → Memoization
- 상향식(top-down) 방식 혹은 하향식(botton-up) 방식으로 구현 가능
탑 다운(top-down) 방식
큰 문제를 해결하기 위해 작은 문제를 호출
- 재귀 함수를 사용하여 문제 해결
- 메모이제이션(Memoization) : 연산 결과를 메모리에 저장해 두었다가 동일한 연산을 반복할 때 이전에 계산 된 결과를 재활용하는 기법
static int[] dp = new int[50];
public static int getFibonacciNumberDP(int n) {
if(n == 0)
return 0;
else if(n == 1)
return 1;
<!-- 1. 확인 : 함수 호출 전 해당 입력에 대한 저장된 결과가 없다면 계산 -->
if(dp[n] == 0) {
<!-- 2. 저장 : 계산 되지 않은 값은 연산 후 특정 자료 구조에 저장 -->
dp[n] = getFibonacciNumberDP(n - 1) + getFibonacciNumberDP(n - 2);
}
<!-- 3. 재활용 : 저장 된 결과가 있다면 다시 계산하지 않고 저장 된 값을 반환 -->
return dp[n];
}바텀 업(botton-up) 방식
가장 작은 문제들부터 답을 구해가며 전체 문제의 답을 찾는 방식
- 재귀 함수를 사용하지 않고 반복문을 통해서 문제 해결
- 타뷸레이션(Tabulation) : 문제를 부분 문제로 나눈 뒤 작은 문제부터 차례로 그 결과를 테이블에 저장하는 방식
static int getFibonacciNumberIter(int n) {
int[] arr = new int[n + 1];
arr[0] = 0;
arr[1] = 1;
if(n == 0) return arr[0];
else if(n == 1) return arr[1];
else {
for(int i = 2; i <= n; i++) arr[i] = arr[i-1] + arr[i-2];
return arr[n];
}
}동적계획법 적용 조건
- 겹치는 부분 문제
- 동일한 작은 문제들이 반복하여 나타나는 경우 -> 점화식으로 표현
- 부분 문제가 반복되지 않는 경우 값을 재사용할 수 없기 때문에 부문 문제가 중복되지 않는 경우 사용 불가능
- 최적 부분 구조
- 문제에 대한 최종 해결 방법은 부분 문제에 대한 최적 문제 해결 방법으로 구성
Tiling(타일 채우기)
2×n 타일을 1×2, 2×1 타일로 채우는 경우의 수
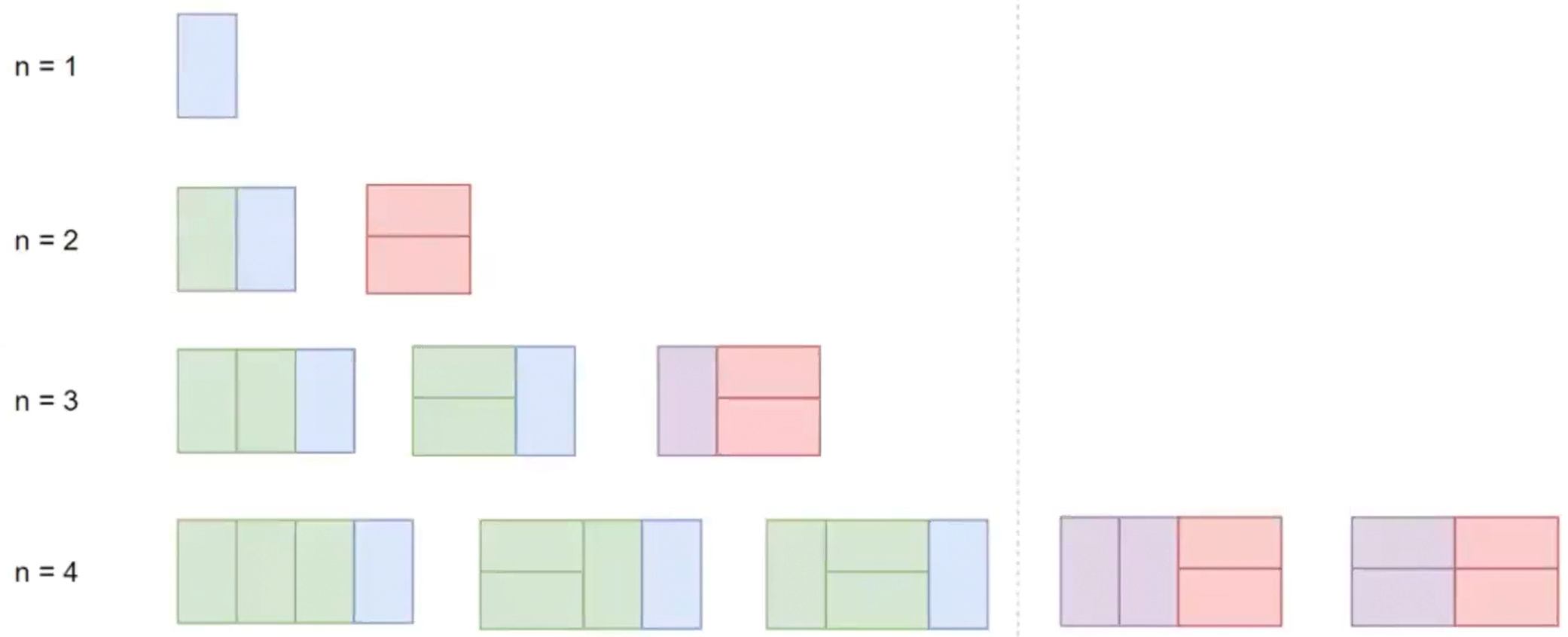
- 점화식: dp[n] = dp[n-1] + dp[n-2]
public static int solution(int n) {
<!-- int 는 큰 값을 넣어서 비교 -->
int[] dp = new int[n + 1];
dp[0] = dp[1] = 1;
for(int i = 2; i <= n; i++) {
dp[i] = dp[i-1] + dp[i-2];
}
return dp[n];
}파도반 수열 (Padovan Sequence)
특정 규칙에 따라 길이가 늘어나는 삼각형의 변의 길이
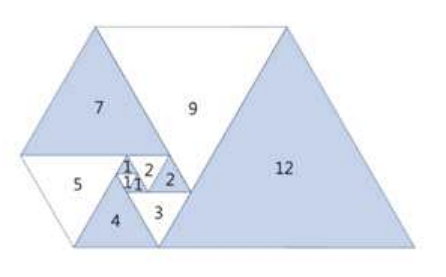
- 점화식 : f(n) = f(n-2) + f(n-3)
<!-- Integer는 null 값으로 비교 -->
static Integer[] dp = new Integer[101];
public static int solution(int n) {
<!-- 초기 값 설정 -->
dp[1] = dp[2] = dp[3] = 1;
<!-- 1. 탑다운 방식 (재귀 호출) -->
return padovan(n);
}
private static int padovan(int n) {
<!-- 연산 해야 하는지 확인 -->
if(dp[n] == null) {
dp[n] = padovan(n - 2) + padovan(n - 3);
}
return dp[n];
}<!-- Integer는 null 값으로 비교 -->
static Integer[] dp = new Integer[101];
public static int solution(int n) {
<!-- 초기 값 설정 -->
dp[1] = dp[2] = dp[3] = 1;
<!-- 2. 바텀업 방식 (반복문) -->
for(int i = 4; i <= n; i++) {
dp[i] = dp[i-2] + dp[i-3];
}
return dp[n];
}
private static int padovan(int n) {
<!-- 연산 해야 하는지 확인 -->
if(dp[n] == null) {
dp[n] = padovan(n - 2) + padovan(n - 3);
}
return dp[n];
}삼각형의 누적 최대값
위에서 아래로 이동하면서 얻을 수 있는 최대 합 구하기
- 마지막 줄에서 가장 큰 값이 정답

- dp[i][j] = max(dp[i-1][j-1], dp[i-1][j]) + t[i][j]
BufferedReader br = new BufferedReader(new StringReader(input));
int n = Integer.parseInt(br.readLine());
<!-- 삼각형 데이터 저장 -->
int[][] t = new int[n + 1][n + 1];
<!-- 내려오면서 가지는 최대 값을 기억할 배열 -->
int[][] dp = new int[n + 1][n + 1];
for(int i = 1; i <= n; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
for(int j = 1; j <= i; j++) {
t[i][j] = Integer.parseInt(st.nextToken());
<!-- dp[i][j]의 값은 dp[i-1][j-1] 또는 dp[i-1][j] 에
기록 된 값 중 큰 값을 선택 한 뒤 현재 값을 누적 연산해서 계산 -->
dp[i][j] = Math.max(dp[i-1][j-1], dp[i-1][j]) + t[i][j];
}
System.out.println(Arrays.toString(t[i]));
}
<!-- dp 배열의 맨 아랫줄에서 최대 값을 구해서 반환 -->
int anwser = 0;
for(int i = 1; i <= n; i++) {
if(anwser < dp[n][i]) anwser = dp[n][i];
}
return anwser;계단오르기
계단 오르기 규칙
1. 계단은 한 번에 1칸 또는 2칸씩만 오를 수 있다.
2. 연속된 세 개의 계단을 모두 밟으면 안된다.
3. 시작점은 계단에 포함되지 않고 마지막 도착 계단은 반드시 밟아야 한다.
public static int solution(String input) throws IOException {
BufferedReader br = new BufferedReader(new StringReader(input));
int n = Integer.parseInt(br.readLine()); // 계단의 개수
<!-- 계단별 점수 -->
int[] arr = new int[n + 1];
<!-- 최적(최대 점수 합계)의 값 누적 -->
int[] dp = new int[n + 1];
for(int i = 1; i <= n; i++) {
arr[i] = Integer.parseInt(br.readLine());
}
<!-- 초기값 설정 -->
dp[1] = arr[1];
if(n >= 2) dp[2] = dp[1] + arr[2];
<!-- 점화식은 3번 계단부터 적용 할 예정 -->
for(int i = 3; i <= n; i++) {
<!-- 가능 상황 1. 직전 계단에서 올라오는 상황
-> 연달아 밟지 않아야 하므로 i-3 -> i-1 -> i 로 이동해야만 함 -->
<!-- 가능 상황 2. 두 계단 전에서 올라오는 상황 -> i-2 전의 상황을 고려할 필요 X -->
<!-- 1번 : dp[i-3] + arr[i-1] vs 2번 : dp[i-2] + arr[i] (현재 계단 점수) -->
dp[i] = Math.max(dp[i-3]+arr[i-1], dp[i-2]) + arr[i];
}
return dp[n];
}Knapsack (분할 불가능 배낭 문제)
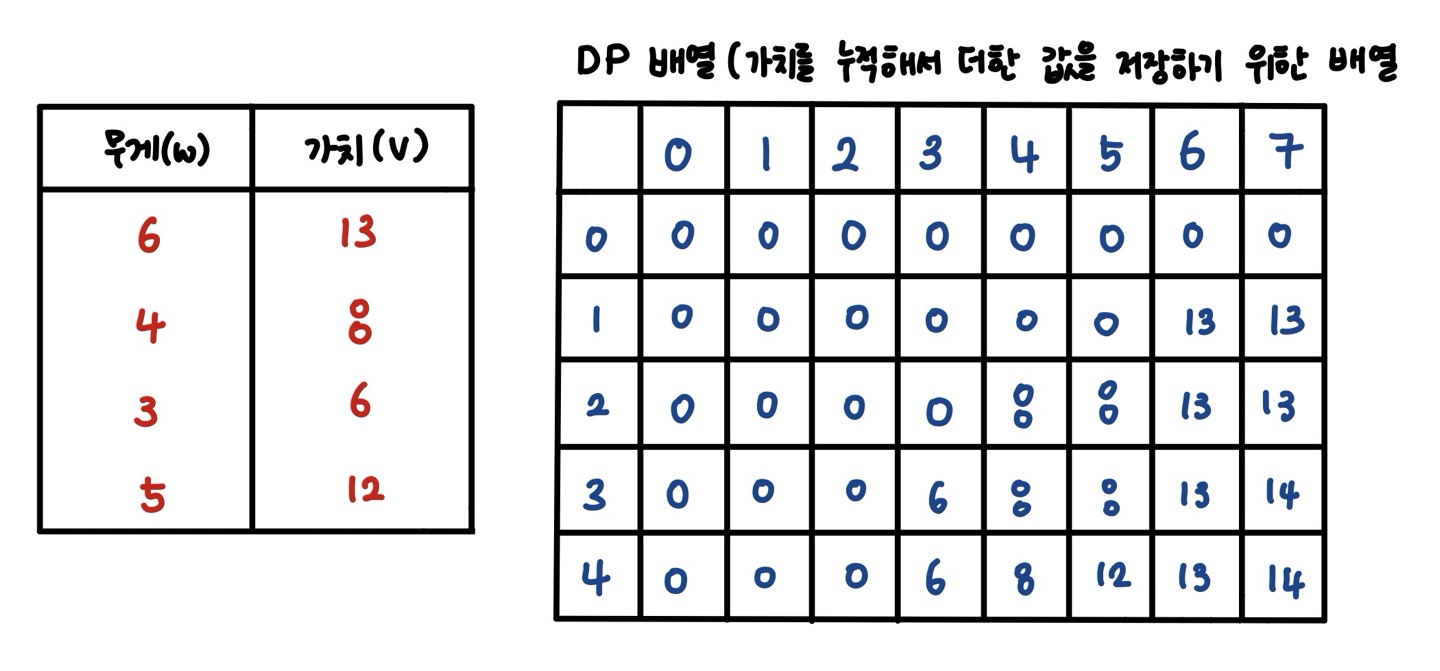
dp 배열에 누적 연산(최대 가치 갱신)을 통해 최적해를 구한다
- 각 물건은 한 번만 선택 가능
- Greedy는 최적해를 보장하지 못한다
v + dp[i-1][j-w]
- 물건 i를 담으려면 무게 w만큼 공간이 필요
- 남은 공간은 j - w
- 현재 물건의 가치 + 남은 공간에 담을 수 있는 최적의 이전 가치
BufferedReader br = new BufferedReader(new StringReader(input));
StringTokenizer st = new StringTokenizer(br.readLine());
<!-- 물건의 개수 -->
int n = Integer.parseInt(st.nextToken());
<!-- 가방 무게 -->
int k = Integer.parseInt(st.nextToken());
<!-- dp[물건인덱스][무게] = 최적 가치값 -->
int[][] dp = new int[n + 1][k + 1];
for(int i = 1; i <= n; i++) {
st = new StringTokenizer(br.readLine());
<!-- 현재 물건의 무게 -->
int w = Integer.parseInt(st.nextToken());
<!-- 현재 물건의 가치 -->
int v = Integer.parseInt(st.nextToken());
<!-- 각 물건에 대한 dp 배열의 행의 값을 채워 나가는 작업
가방의 키로수까지 반복 -->
for(int j = 1; j <= k; j++) {
<!-- 물건이 가방에 들어갈 수 있는지 확인 -->
if(j < w) {
<!-- 1. 들어갈 수 없는 경우 : 가치값의 변화가 없으므로 이전 행의 값을 그대로 반영 -->
dp[i][j] = dp[i-1][j];
} else {
<!-- 2. 들어갈 수 있는 경우 :
담는다 : 물건 가치 + 해당 무게 빼고 남는 가치
안 담는다 : 이전 행의 값 -> 두 가지를 비교해서 높은 값을 반영 -->
dp[i][j] = Math.max(v + dp[i-1][j-w], dp[i-1][j]);
}
}
}
return dp[n][k];Fractional Knapsack (분할 가능 배낭 문제)
- 물건을 쪼갤 수 있음 (부분 담기 가능)
- 가치/무게 비율을 기준으로 Greedy 방식 적용
- 정렬 또는 우선순위 큐 사용하여 가성비(가치/무게)가 높은 순서대로 담는다
- 남은 용량이 부족할 경우 → 해당 물건을 분할해서 일부만 넣는다
- Greedy 방식으로 항상 최적해를 구할 수 있음
LIS(Longest Increasing Subsequence) : 최대 부분 증가 수열
주어진 수열에서 원래의 순서를 유지하면서, 증가하는 순서를 만족하는 부분 수열 중 가장 긴 길이를 찾는 문제
BufferedReader br = new BufferedReader(new StringReader(input));
int n = Integer.parseInt(br.readLine());
int[] arr = new int[n + 1];
int[] dp = new int[n + 1];
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 1; i <= n; i++) {
arr[i] = Integer.parseInt(st.nextToken());
<!-- 자기 자신 하나만으로도 길이 1의 수열이 되므로 초기값은 1 -->
dp[i] = 1;
}
int max = 1;
<!-- 입력 된 arr 배열의 각 인덱스를 기준 삼아 앞으로 탐색할 반복문 -->
for(int i = 1; i <= n; i++) {
for(int j = 1; j < i; j++) {
<!-- i : 현재 기준 인덱스, j : 이전의 인덱스들과 비교 -->
if(arr[i] > arr[j]) {
<!-- 현재 값은 증가 수열의 일부라고 판단 dp[i] = dp[j] + 1
10(1) 20(2) 10(1) 30 -> 2 + 1 = 3이 30에 들어갈 수 있도록 하려면
dp[i]와 dp[j]+1 중 큰 값을 골라서 계속 업데이트 해야 한다. -->
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
<!-- 마지막 값으로 출력하게 되면 가장 마지막 값이 감소하는 경우 최대값으로 나오지 않는다.
따라서 모든 동작이 완료된 후 가장 큰 값을 찾아줘야 한다. -->
max = Math.max(max, dp[i]);
}
return max;LCS(Longest Common Subsequence) : 최장 공통 부분 수열
두 개의 문자열(또는 수열)에서, 각 문자열의 원래 순서를 유지하면서 공통으로 나타나는 부분 수열 중에서 가장 긴 수열을 찾는 문제
- 연속될 필요 없다
- 예를 들어, 문자열 "ABCBDAB"과 "BDCABA"가 주어졌을 때, 공통 부분 수열인 "BCBA" 또는 "BDAB" 등이 있을 수 있으며, 이들 중 길이가 가장 긴 수열을 찾는다.
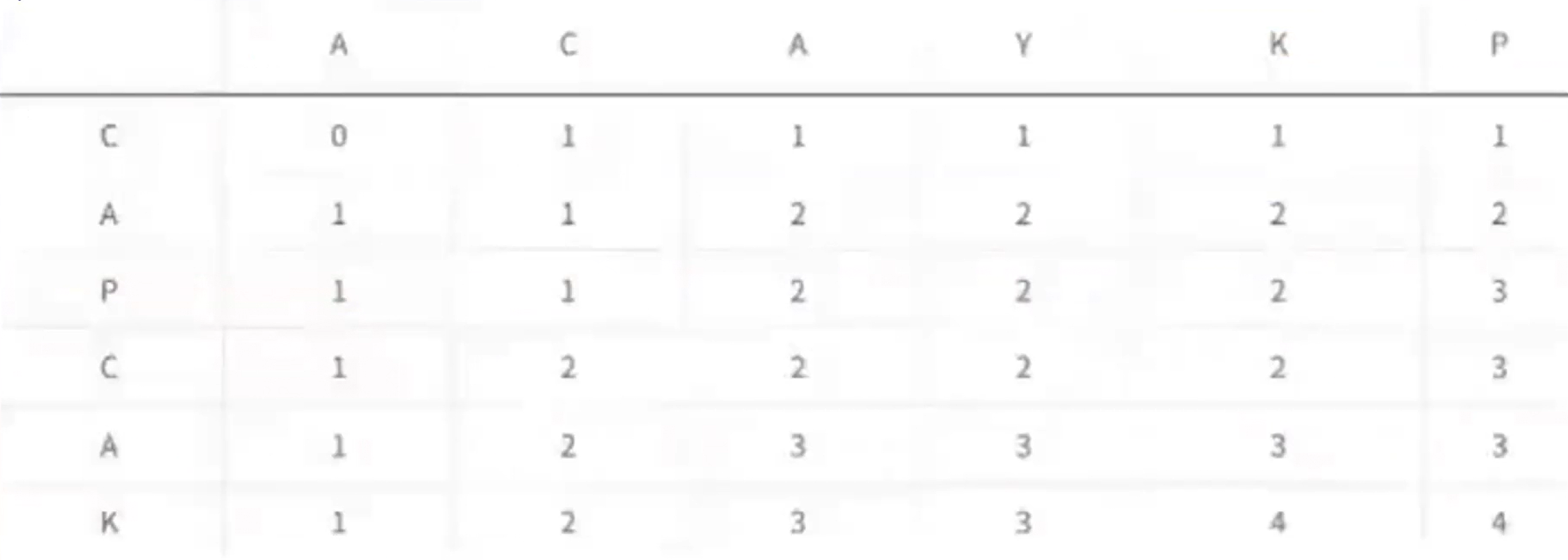
static char[] arr1;
static char[] arr2;
static Integer[][] dp;
public static int solution(String input) throws IOException {
BufferedReader br = new BufferedReader(new StringReader(input));
arr1 = br.readLine().toCharArray();
arr2 = br.readLine().toCharArray();
dp = new Integer[arr1.length][arr2.length];
<!-- 탑 다운 방식 (재귀 호출) -->
return lcs(arr1.length-1, arr2.length-1);
}
static int lcs(int x, int y) {
<!-- 재귀 호출 종료 조건 - 문자열 범위를 벗어나면 0 -->
if(x < 0 || y < 0) return 0;
<!-- 연산 되어 있지 않은 경우에만 연산을 수행 -->
if(dp[x][y] == null) {
if(arr1[x] == arr2[y]) {
<!-- 서로 같은 문자가 발견 되는 경우
이전까지의 문자열의 최적해 값이 x-1, y-1 인덱스에 있고 1을 추가 -->
dp[x][y] = lcs(x-1, y-1) + 1;
} else {
<!-- 같은 문자가 아닌 경우
x 방향 또는 y 방향에서 큰 값을 반영한다 -->
dp[x][y] = Math.max(lcs(x-1, y), lcs(x, y-1));
}
}
return dp[x][y];
}<!-- Bottom-up 방식 -->
for (int i = 1; i <= arr1.length; i++) {
for (int j = 1; j <= arr2.length; j++) {
if (arr1[i - 1] == arr2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
