2025.04.03,
DataStructure
복잡도
복잡도에 따른 표기법
- Big-O 표기법 (Big-O notation) : 최악의 경우를 산정해서 분석 (일반적)
- Big-Ω 표기법 (Big-Omega notation : 최선의 경우를 산정해서 분석
- Big-θ 표기법 (Big-Theta notation) : 위 두경우의 평균을 산정해서 분석
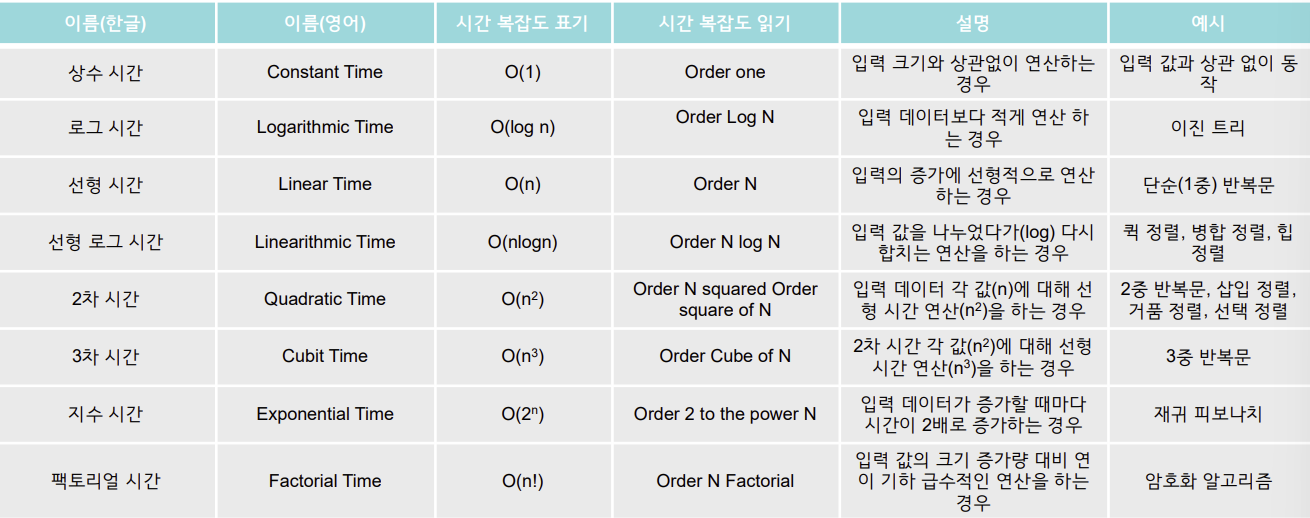
시간 복잡도
로직이 실행되는데 입력 값에 걸리는 시간
- 입력 값과 문제를 해결하는 데 걸리는 시간을 함수 관계로 나타낸 것(input에 따른 시간 증가도)
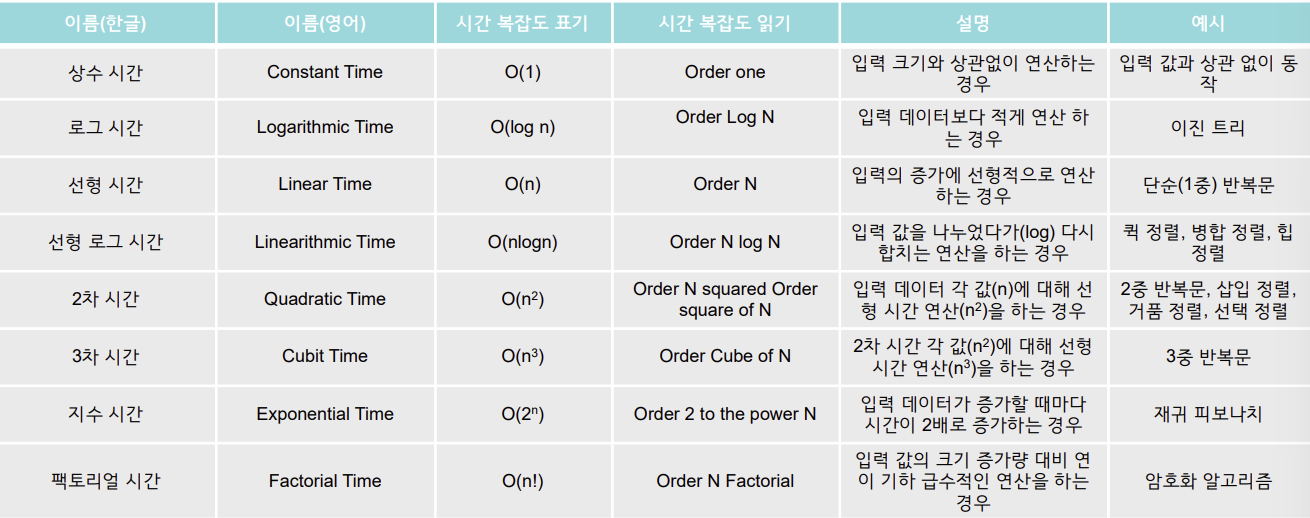
- 로그, 선형, 선형 로그, 2차, 지수 시간은 알아두는 것이 좋다.
로그 시간 O(log n) 이진 트리
public static int binarySearch(int[] arr, int target){
<!-- 초기 세팅 배열 오름차순 -->
Arrays.sort(arr);
<!-- 배열의 처음과 끝을 지정하는 인덱스 번호 변수 -->
int left = 0, right = arr.length -1;
while (left <= right){
int mid = left + (right - left) / 2;
<!-- 타겟과 mid 값이 일치하는 경우
if (target == arr[mid]){
return mid;
<!-- 타겟보다 mid 값이 작으면 현재 mid의 하나 큰 값으로 이동한다. -->
} else if (arr[mid] < target) {
left = mid + 1;
<!-- 타겟보다 mid 값이 크면 현재 mid의 하나 작은 값으로 이동한다. -->
} else {
right = mid -1;
}
}
return -1;
}선형 시간 복잡도 O(n) 단순(1중) 반복문
public static int[] reverse(int[] arr){
int[] reversed = new int[arr.length];
for (int i = 0; i < arr.length; i++){
reversed[i] = arr[arr.length -1 -i];
}
return reversed;
}지수 시간 복잡도 O(2^n) 재귀 피보나치
public static int fibonacci(int n){
<!-- n 이 0 또는 1인 경우 -->
if(n<=1){
return n;
}
return fibonacci(n-1) + fibonacci(n-2);
}시간 복잡도를 구하는 요령
- 하나의 루프를 사용하여 단일 요소 집합을 반복하는 경우 : O(n)
- 컬렉션의 절반 이상을 반복하는 경우 : O(n/2) -> O(n)
- 두 개의 다른 루프를 사용하여 두 개의 개별 컬렉션을 반복하는 경우 : O(n+m)-> O(n)
- 두 개의 중첩 루프를 사용하여 단일 컬렉션을 반복하는 경우 : O(n^2)
- 컬렉션 정렬을 사용하는 경우 : O(n*log(n))
공간 복잡도
로직 연산에 사용되는 메모리 공간으로 총 공간 요구 = 고정 공간 요구 + 가변 공간 요구
- 얼마나 많은 메모리 공간을 사용하는지 확인
- 고정 공간 : 알고리즘과 무관하게 요구되는 공간
- 가변 공간 : 알고리즘과 밀접한 공간
List
순서가 있는 데이터의 집합
- 인덱스나 포인터로 접근할 수 있는 자료구조
ArrayList
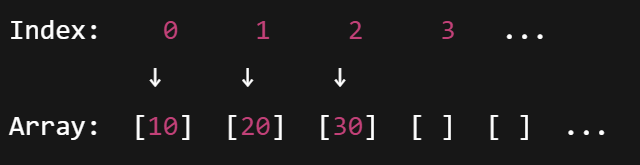
- index, value 형식으로 저장됨
- 출력 시 [요소1, 요소2, ...] 형식으로 출력
- 정적 데이터를 저장하고 순차적으로 접근할 때 사용
- 인덱스를 이용해 O(1) 시간 복잡도로 빠르게 접근 가능
- 연속된 메모리 공간을 사용하므로 캐시 히트율이 높아 성능이 좋음
- 처음 할당된 크기를 변경하기 어렵고, 크기를 늘리려면 새 배열 생성 후 기존 데이터 복사 필요
- 중간에 데이터를 추가하거나 삭제할 때 데이터 이동이 필요해 O(n) 시간이 걸림
List<Integer> list = new ArrayList<>();
<!-- 요소 추가 -->
list.add(E e); // 리스트 끝에 요소 추가
list.add(int index, E e); // 특정 위치에 요소 삽입
<!-- 요소 조회 -->
list.get(int index); // 해당 인덱스의 요소 반환
<!-- 요소 제거 -->
list.remove(int index); // 해당 인덱스 요소 제거 및 뒤 요소 이동
<!-- 리스트 크기 -->
list.size(); // 현재 요소 개수 반환
<!-- 요소 여부 확인 -->
list.isEmpty(); // 요소가 비어 있는지 확인
<!-- 초기화 -->
list.clear(); // 리스트 전체 비우기
LinkedList

- Head(머리) 노드: 연결 리스트의 시작점
- Tail(꼬리) 노드: 마지막 노드, 다음 노드가 null
- 출력 시 [요소1, 요소2, ...] 형식으로 출력
- 동적 데이터 관리, 삽입과 삭제가 빈번한 경우에 사용
- 각 노드는 데이터 + 다음 노드를 가리키는 포인터로 구성
- 동적으로 노드를 추가/삭제할 수 있어 메모리를 효율적으로 사용 가능
- 중간에 데이터를 추가하거나 삭제할 때 이동할 필요 없이 포인터만 변경하면 됨 (O(1) 또는 O(n) – 위치 찾기 필요)
- 원하는 데이터를 찾으려면 처음부터 순차적으로 탐색해야 하므로 O(n) 시간이 걸림
- 각 노드가 데이터 외에도 다음 노드를 가리키는 포인터를 저장해야 하므로 메모리 오버헤드가 발생함
List<Integer> list2 = new LinkedList<>();
<!-- 요소 추가 -->
list2.add(E e); // 리스트 끝에 요소 추가
list2.add(int index, E e); // 특정 위치에 요소 삽입
<!-- 요소 조회 -->
list2.get(int index); // 해당 인덱스의 요소 반환
<!-- 요소 제거 -->
list2.remove(int index); // 해당 인덱스 요소 제거 및 뒤 요소 이동
<!-- 리스트 크기 -->
list2.size(); // 현재 요소 개수 반환
<!-- 요소 여부 확인 -->
list2.isEmpty(); // 요소가 비어 있는지 확인
<!-- 초기화 -->
list2.clear(); // 리스트 전체 비우기Stack
LIFO(Last In, First Out) 방식으로 데이터를 관리하는 자료구조
- Vector 클래스를 상속
- Vector는 내부적으로 배열을 사용하여 데이터를 저장
- 출력 시 [요소1, 요소2, ...] 형식으로 출력, 마지막 값이 top
- top: 스택의 가장 위 요소 (맨 마지막에 들어온 값)
- 배열의 동적 크기 조정 기능을 활용하여 스택의 요소를 관리
- 함수 호출 관리 : 함수 호출 시 반환 주소를 저장하고 복귀 시 사용
- 연산자 우선순위 처리 : 계산기나 컴파일러에서 연산자 우선순위를 처리할 때 사용
- 현재 잘 사용하진 않는다.
Stack<Integer> stack = new Stack<>();
<!-- 요소 추가 -->
stack.push(E e);
<!-- 요소 조회 -->
stack.peek(); //스택의 맨 위 데이터를 제거하지 않고 반환
<!-- 요소 제거 -->
stack.pop(); // 스택의 맨 위 데이터를 제거하고 반환
<!-- 스택 비어있는지 확인 -->
stack.isEmpty();
<!-- 스택 크기 -->
stack.size();
<!-- 초기화 -->
stack.clear();
ArrayStack

배열 기반으로 스택을 구현
- 배열을 사용해 데이터를 저장
- top : 스택의 상단 인덱스
- 자바에서 기본 제공하지 않기 때문에 ArrayStack은 직접 구현해야 사용 가능함
LinkedListStack

연결 리스트 기반으로 스택을 구현
- 각 요소가 Node로 구성, 포인터로 연결
- top은 항상 head (가장 최근 삽입된 노드)
- 인덱스로 직접 접근 불가
- 자바에서 기본 제공하지 않기 때문에 LinkedListStack은 직접 구현해야 사용 가능함
알고리즘 문제 풀이
-> 배열을 사용한다?
-> 첫 요소, 끝 요소, 중간 요소 변수를 미리 선언해 놓는다.
-> 스택을 사용한다?
-> 탑 요소를 어떻게 관리 할 것인가?
Queue
FIFO(First In, First Out) 방식으로 데이터를 관리하는 자료구조
- 작업 스케줄링 : 운영 체제에서 작업을 순차적으로 처리할 때 사용
- 데이터 스트림 처리 : 네트워크 데이터 패킷을 순차적으로 처리할 때 사용
- 출력 시 [요소1, 요소2, ...] 형식으로 출력
ArrayQueue
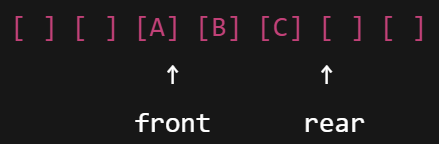
자바 표준 라이브러리에는 존재하지 않기 때문에 직접 구현해야 한다
- 배열 기반으로 만든 큐 구현체
- 일반적으로 순환 큐(원형 큐) 구조를 사용하여 공간 낭비를 방지
- 사용자의 입장에서 원형 큐처럼 동작하지는 않는다- ArrayDeque는 크기가 가득 차면 자동으로 확장
- front와 rear 인덱스를 관리
- 삭제 : front, 삽입 : rear
LinkedListQueue
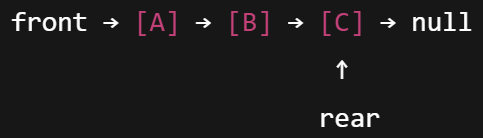
- 각 요소가 Node로 구성, 포인터로 연결
- 삭제 노드 : front, 삽입 노드 : rear
Queue<Integer> queue = new LinkedList<>();
<!-- 요소 추가 -->
queue.offer(E e); // 큐의 끝에 요소 추가 (성공 여부 반환)
<!-- 요소 조회 -->
queue.peek(); // 큐의 맨 앞 요소를 제거하지 않고 반환 (비어있으면 null)
<!-- 요소 제거 -->
queue.poll(); // 큐의 맨 앞 요소를 제거하고 반환 (비어있으면 null)
<!-- 큐 비어있는지 확인 -->
queue.isEmpty();
<!-- 큐 크기 -->
queue.size();
<!-- 초기화 -->
queue.clear();Deque
양쪽 끝에서 삽입과 삭제를 허용하는 자료구조
- front와 rear 인덱스를 관리
- front : 삭제/삽입 가능, rear : 삭제/삽입 가능
- 스크롤/문서 편집기: undo/redo 기능
- 웹 브라우저: 방문 기록 관리
- 스케줄링: 양방향 큐를 통한 작업 관리
- 출력 시 [요소1, 요소2, ...] 형식으로 출력
ArrayDeque
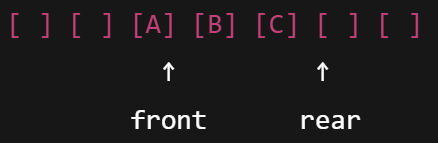
순환 배열을 사용하여 양쪽 끝에서의 삽입과 삭제를 효율적으로 처리
Deque<Integer> deque = new ArrayDeque<>();
<!-- 요소 추가 -->
deque.addFront(E e); // 데이터 x를 덱의 앞쪽에 추가
deque.addRear(E e); // 데이터 x를 덱의 뒤쪽에 추가
<!-- 요소 조회 -->
deque.getFront(); // 덱의 앞쪽 데이터를 반환 (제거하지 않음)
deque.getRear(); // 덱의 뒤쪽 데이터를 반환 (제거하지 않음)
<!-- 요소 제거 -->
deque.deleteFront(); // 덱의 앞쪽에서 데이터를 제거
deque.deleteRear(); // 덱의 뒤쪽에서 데이터를 제거
<!-- 큐 비어있는지 확인 -->
deque.isEmpty();
<!-- 큐 크기 -->
deque.size();
<!-- 초기화 -->
deque.clear();LinkedListDeque

Tree
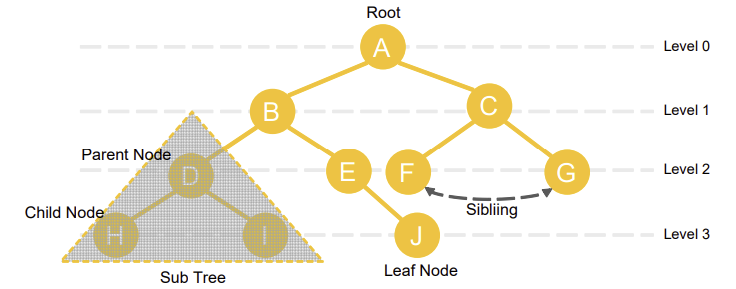
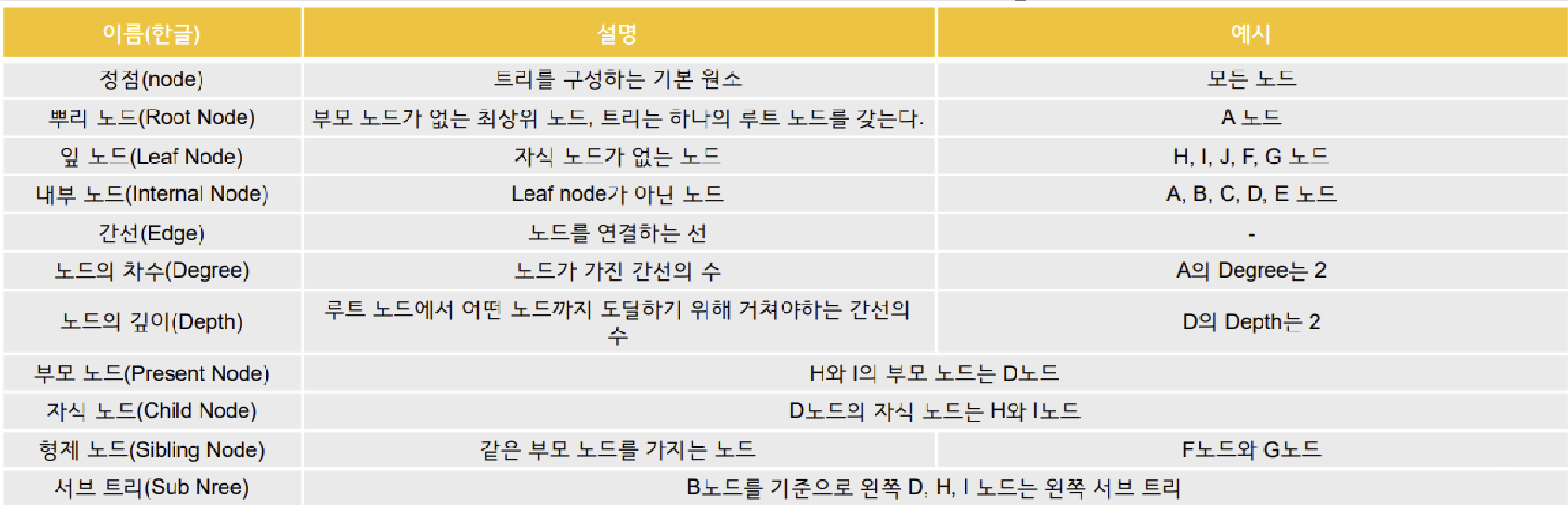
계층적인 구조로 노드와 자식 노드들로 구성된 자료구조
정점과 간선으로 연결된 그래프의 특수한 형태(그래프의 부분 집합)
- 그래프와 다르게 부모-자식 개념을 가지는 비순환적 경로로 연결되어 있다.
- 이진 트리: 각 노드가 최대 두 개의 자식을 가지는 트리 구조
- AVL 트리: 높이 균형을 유지하는 이진 탐색 트리
- 레드-블랙 트리: 색상 속성을 사용하여 균형을 유지하는 이진 탐색 트리
- B-트리: 다중 자식을 가지는 트리로, 디스크 I/O를 최소화하여 대량의 데이터를 효율적
으로 관리 - Java Collection Framework에서는 TreeSet, TreeMap 등에서 트리 구조를 활용하고 있는데 내부적으로 레드-블랙 트리로 관리
- 이진 트리를 가장 많이 사용한다.
- 알고리즘 문제에서 트리를 단독으로 사용하는 문제는 많이 없지만 greedy, dp에서 트리 개념이 사용된다.
이진 트리
각 노드가 최대 두 개의 자식을 가지는 트리 구조
- 왼쪽 자식과 오른쪽 자식으로 구성
- 모든 트리의 기본 형태
Skewed Binary Tree(편향 이진 트리)
노드들이 한쪽(왼쪽/오른쪽)으로만 연결
- 구조적으로 연결 리스트처럼 동작 -> 굳이 트리로 작성하는 것이 의미가 없음
Balanced Binary Tree(균형 이진트리)
왼쪽과 오른쪽 서브트리의 높이 차이가 최소
- AVL 트리, 레드-블랙 트리
포화 이진 트리
트리의 높이가 모두 일정하며 리프 노드가 꽉찬 트리
- 모든 리프 노드가 같은 level에 위치
완전 이진 트리
마지막 레벨을 제외하고 노드들이 완전히 채워져 있고, 마지막 레벨은 왼쪽부터 채워진 트리
이진 탐색 트리(BST)
이진 트리의 구조를 가지면서 추가로 왼쪽 서브트리의 모든 노드는 현재 노드 값 보다 작고, 오른쪽 서브 트리의 모든 노드는 현재 노드 값보다 크다는 규칙(정렬 속성)을 만족
- 왼쪽 노드와 오른쪽 노드로 구성
- 이진 트리 구조 + 정렬 속성(왼쪽<루트<오른쪽)
전위 순회 (Preorder)
트리를 복사, 전위 표기법을 구하는데 주로 사용
- 루트 → 왼쪽 → 오른쪽
public void preOrder(Node node) {
if(node != null) {
System.out.print(node.data + " ");
if(node.left != null) preOrder(node.left);
if(node.right != null) preOrder(node.right);
}
}중위 순회 (Inorder)
이진 탐색트리에서 오름차순/내림차순으로 값을 가져올 때 주로 사용
- 왼쪽 → 루트 → 오른쪽
public void inOrder(Node node) {
if(node != null) {
if(node.left != null) inOrder(node.left);
System.out.print(node.data + " ");
if(node.right != null) inOrder(node.right);
}
}후위 순회 (Postorder)
트리를 삭제할 때 주로 사용
- 왼쪽 → 오른쪽 → 루트
public void postOrder(Node node) {
if(node != null) {
if(node.left != null) postOrder(node.left);
if(node.right != null) postOrder(node.right);
System.out.print(node.data + " ");
}
}레드-블랙 트리
균형 잡힌 이진 탐색 트리
- 각 노드에 색상을 부여하여 균형 유지
- 루트 노드 : 블랙, 레드노드의 자식 노드는 모두 블랙
- 모든 경로에서 루트부터 리프 노드까지의 블랙 노드 수는 동일
- 모든 리프 노드는 블랙
TreeSet
중복 불허, 자동정렬(기본은 오름차순)
TreeSet<Integer> set = new TreeSet<>();
<!-- 삽입 -->
set.add(value);
<!-- 삭제 -->
set.remove(value);
<!-- 포함 여부 확인 -->
set.contains(value);
<!-- 비어있는지 확인 -->
set.isEmpty();
<!-- 요소 개수 확인 -->
set.size();
<!-- 초기화 -->
set.clear();TreeMap
키를 기준으로 정렬되는 map
- 삽입 시 자동으로 키 기준 정렬
- 내부적으로 레드-블랙 트리 기반 BST구조
TreeMap<Integer, String> map = new TreeMap<>();
<!-- 삽입 -->
map.put(key, "value");
<!-- 삭제 -->
map.remove(key);
<!-- 키 존재 여부 확인 -->
map.containsKey(key);
<!-- 키에 해당하는 값 조회 -->
map.get(key);
<!-- 비어있는지 확인 -->
map.isEmpty();
<!-- 요소 개수 확인 -->
map.size();
<!-- 초기화 -->
map.clear();Heap
완전 이진 트리 구조를 가지며, 우선순위 큐를 구현하기 위한 자료구조
- Java Collection Framework 에서 heap을 직접 지원하는 클래스는 없다
- PriorityQueue 클래스를 이용하여 heap을 구현
- 배열을 사용하여 힙을 구현
- 부모-자식 노드 간의 인덱스 관계를 이용해 데이터에 접근
- 우선순위 큐: 작업의 우선순위를 기준으로 데이터를 관리
- 정렬 알고리즘: 힙 정렬을 통해 데이터를 정렬
- 스케줄링: 작업 스케줄링에서 우선순위에 따라 작업을 처리
PriorityQueue<Integer> heap = new PriorityQueue<>();
<!-- 요소 추가 -->
heap.offer(value);
<!-- 큐에서 가장 앞에 있는 값 조회 -->
<!-- PriorityQueue는 기본이 최소 힙, 작은 값이 먼저 나옴
숫자가 작을수록 우선순위가 높다 -->
heap.peek();
<!-- 삭제하면서 반환 -->
heap.poll();
<!-- 비어있는지 확인 -->
heap.isEmpty();
<!-- 요소 개수 확인 -->
heap.size();
<!-- 전체 초기화 -->
heap.clear();- 최대합으로 조회
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Collections.reverseOrder());
or
<!-- 사용자 정의 정렬기준
PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);Graph
정점(node 또는 vertex)과 간선(edge)으로 이루어진 자료구조
- 다양한 관계와 경로를 표현
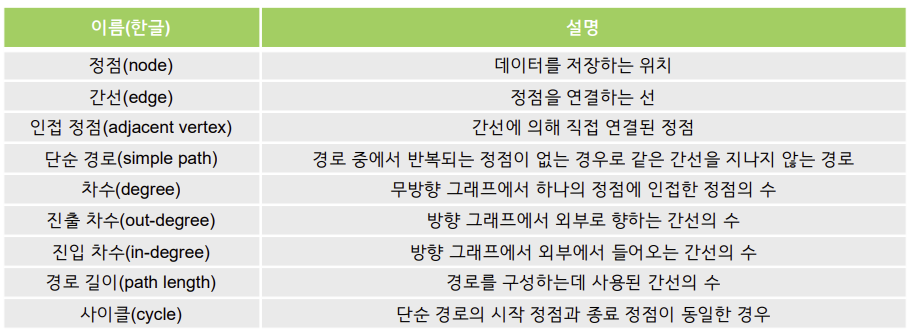
그래프 종류
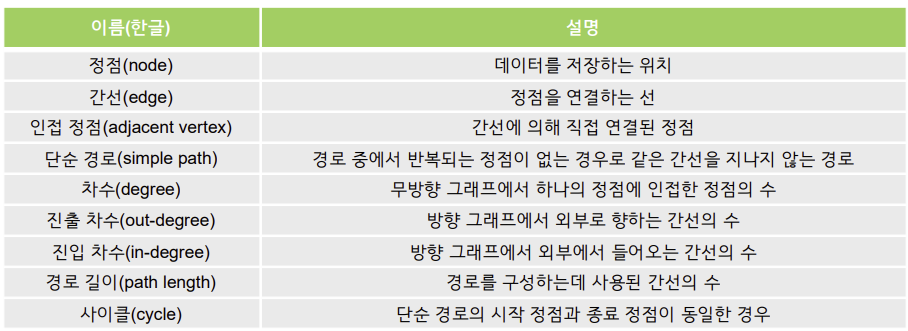
- 무방향 그래프 : 두 정점을 연결하는 간선에 방향이 없다.
- 방향 그래프 : 두 정점을 연결하는 간선에 방향이 있고 간선이 가리키는 방향으로만 이동 기능
- 가중치 그래프 : 두 정점을 이용할 때 비용이 드는 그래프
그래프의 연산
인접 행렬
2차원 배열을 사용하여 노드 간의 연결 관계를 표현
- 노드와 간선의 개수가 많지 않고, 노드 간의 연결 여부를 빠르게 확인해야 하는 경우 사용
인접 리스트
각 노드에 연결된 노드 목록을 리스트로 표현
- 노드의 개수가 많고, 각 노드에 연결된 간선의 수가 적은 경우 사용
트리와 그래프의 비교

참고
인텔리제이 디버그 모드 단축키
- 디버그 모드 실행 : 벌레모양 / shift + F9
- 한줄씩 내려가면서 실행 단축키 : F8
- 참조하는 메소드나 호출되는 메소드 확인 : F7