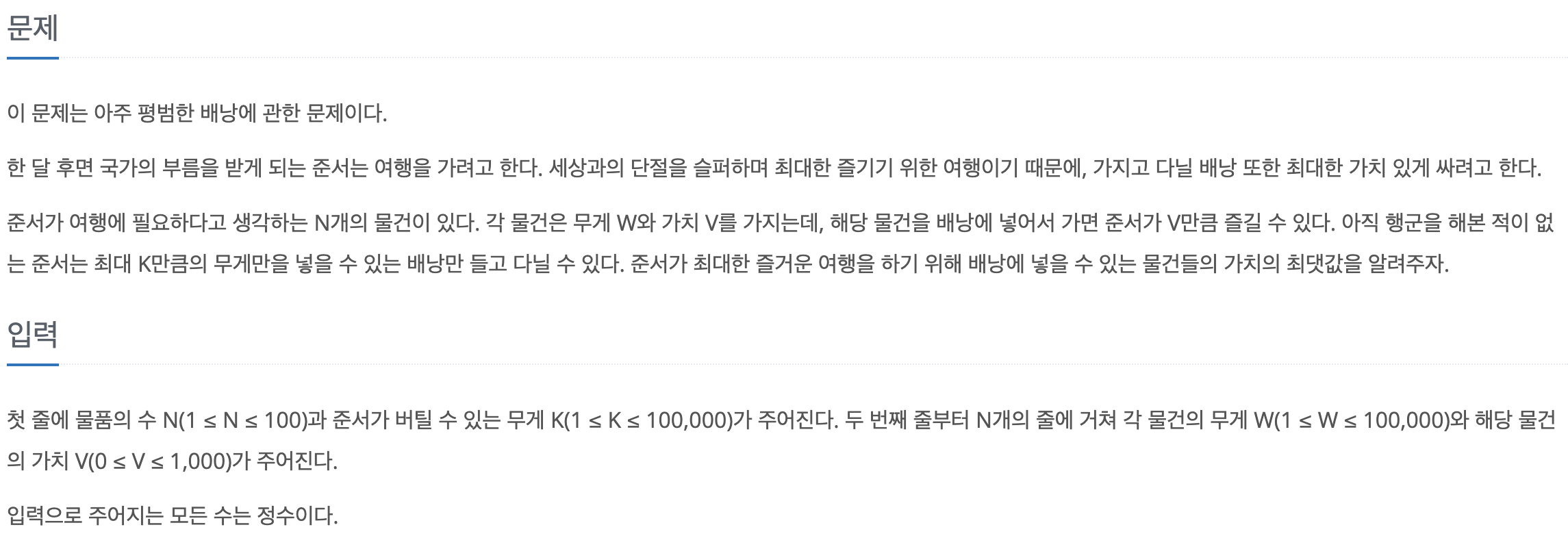
📖문제

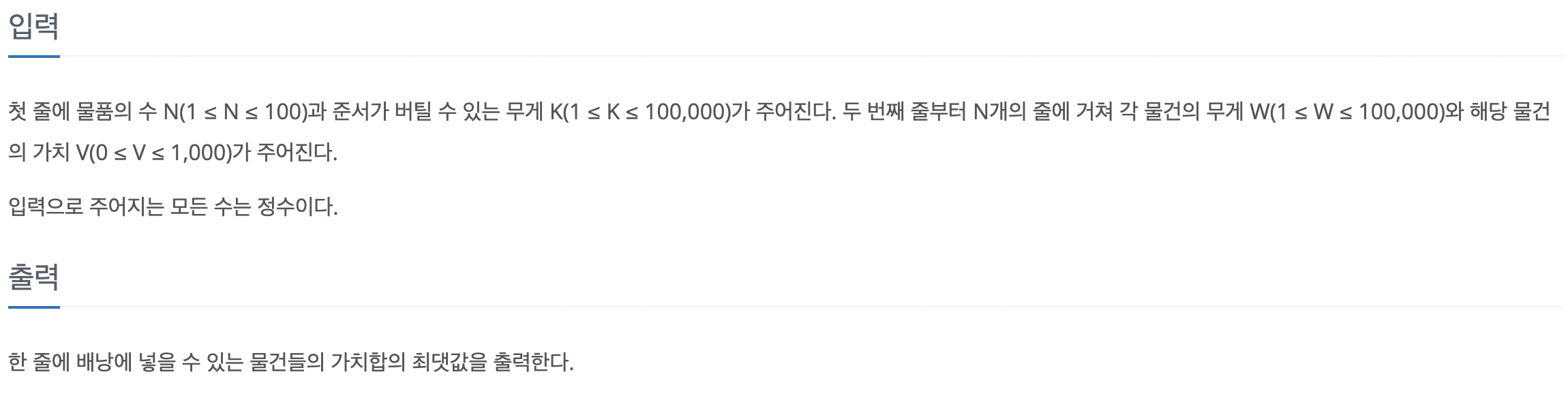
💡입&출력 예시

❓접근

동적 프로그래밍(Dynamic Programming)을 책으로 공부할 때 나온다는 대표적인 문제이다.
(배낭에 넣을 물건들은 잘라서 넣을 수 없는 0-1 Knapsack 문제)

문제에 대한 이해를 위해

가로 축 : 가방이 넣을 수 있는 무게(K까지)
세로 축 : 넣어야하는 물건의 무게

인 표를 작성했다.

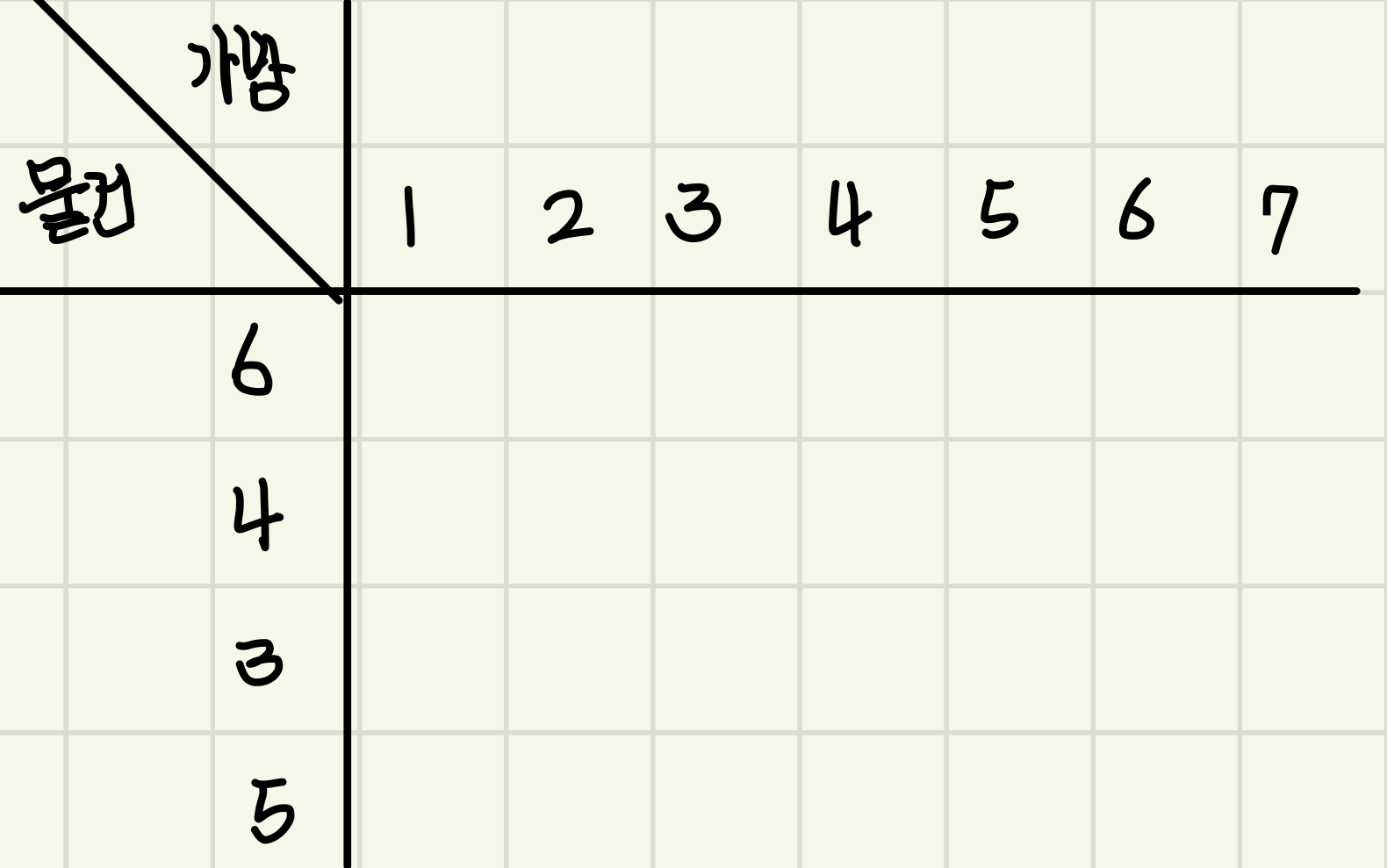
표 내부는 무게가 6, 4, 3, 5kg인 물건을 순서대로 넣어가며 해당 가방에 넣을 수 있는 가방의 최대 가치 값을 구해 볼 것이다.

1단계 : 6kg인 물건을 가방에 넣을 때

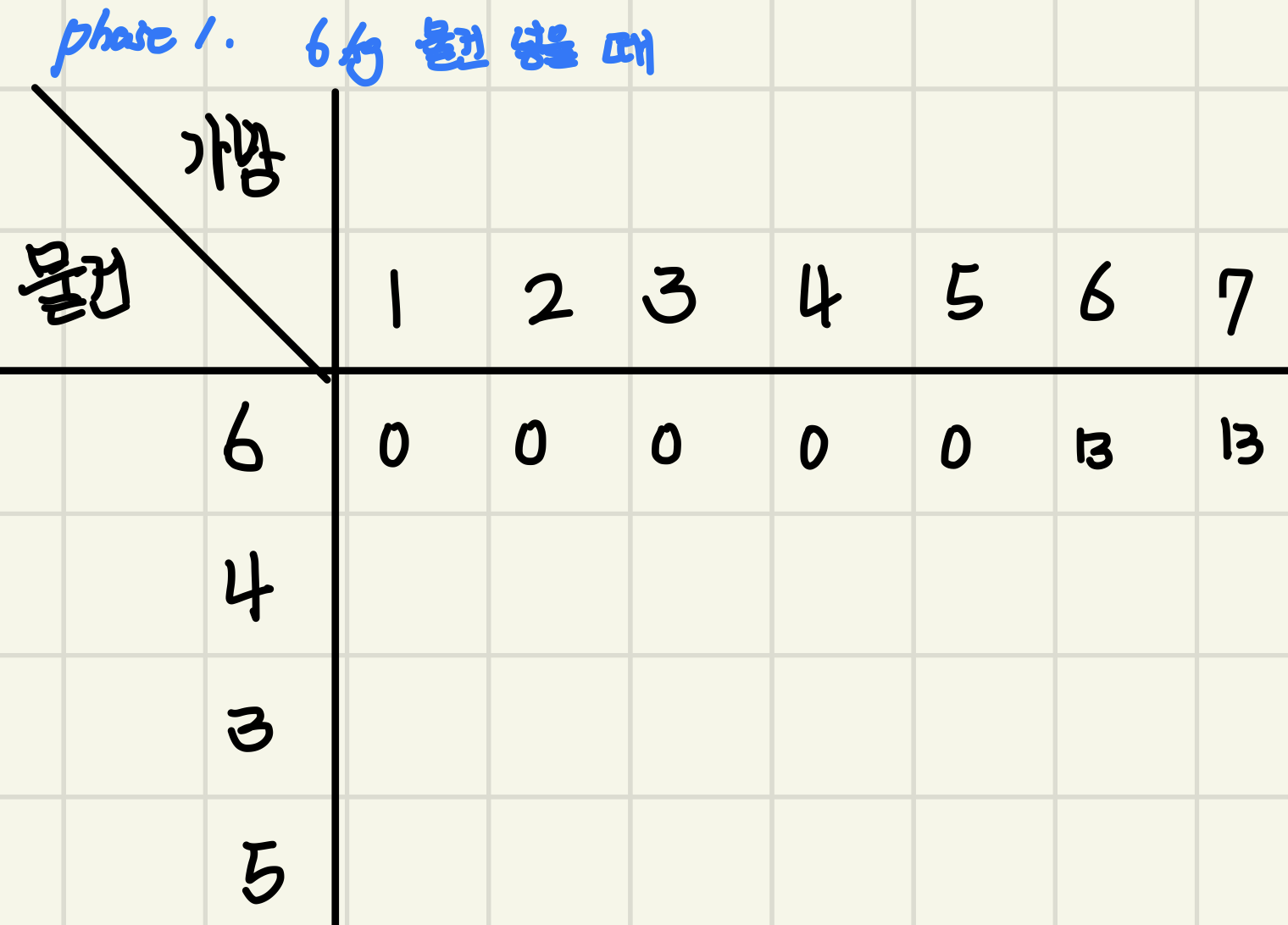
1단계는 6kg인 물건을 넣는데 6, 7가방에만 물건이 들어가므로 해당 가방에 넣은 물건의 값을 기입한다.

2단계 : 4kg인 물건을 가방에 넣을 때

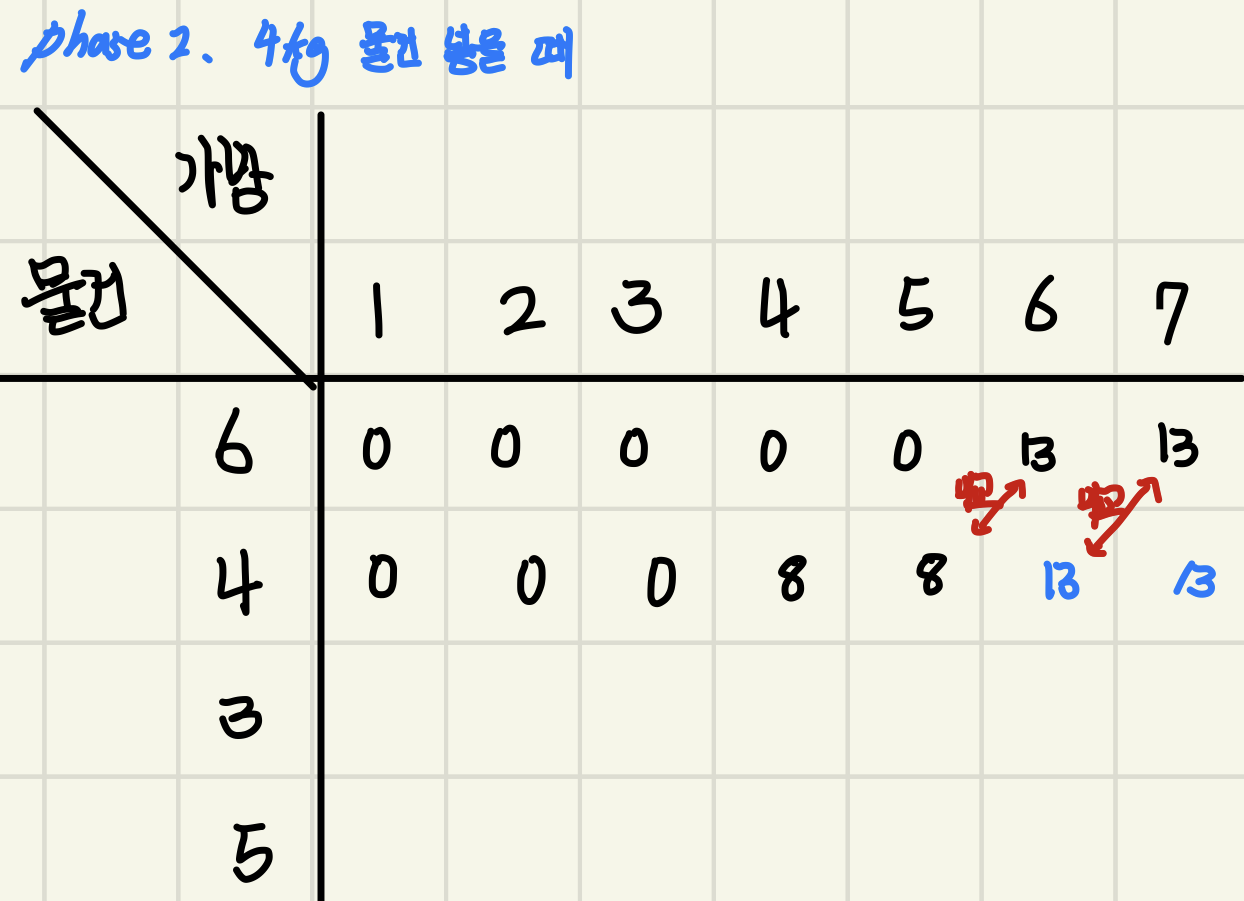
4kg인 가방을 넣을 때 4,5가방엔 4kg인 무게만 들어가므로 4,5가방의 최대 값는 8이지만, 6,7 가방은 앞서 1단계의 값이 더 크기 때문에 13을 기입해준다.

이를 코드로 나타내면 다음과 같다.

table[행][열] = max(table[행-1][열], 현재 값))

### 3단계 : 3kg인 물건을 가방에 넣을 때  3kg인 물건은 7인 가방에서 3kg물건과, 4kg인 물건을 동시에 넣을 수 있기에 두개 합친 값을 이전 2단계 7인 가방 값과 비교를 해줘야 한다. 이 때 4kg인 물건의 값은

이를 코드로 나타내면 다음과 같다.

table[행][열] = max(table[행-1][열], table(table[행-1][열-현재 무게]+현재 값))

4단계 : 5kg인 물건을 가방에 넣을 때

5kg인 물건은 동시에 넣을 수 있는 물건이 없으므로, 1,2단계와 동일하게 앞 단계의 값들과 비교해주면서 최신화해주면 된다.

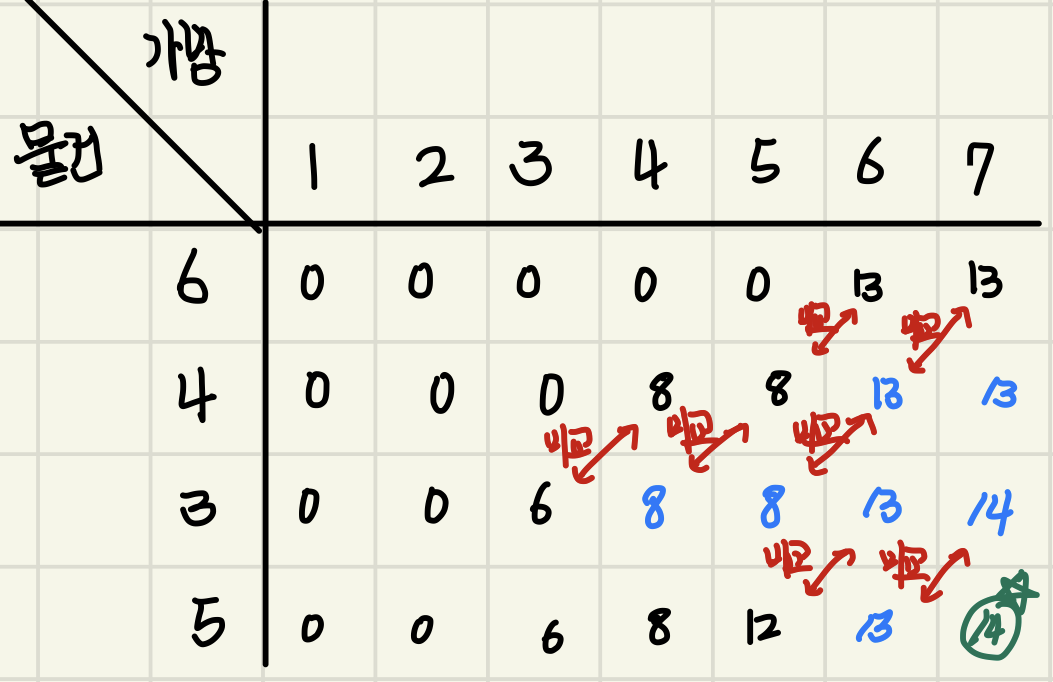
마지막 단계이므로 이 표의 가장 마지막 값이 우리가 원하는 배낭에 넣을 수 있는 최대 가치 값이다!!!!

🖥 코드

import sys
input = sys.stdin.readline

n, k = map(int, input().split())
item = [[0,0]]
#배낭에 넣을 물건들
for i in range(n):
    item.append(list(map(int, input().split())))
dp = [[0] * (k+1) for _ in range(n+1)]
#앞서 설명한 테이블
for i in range(1, n+1):
    for j in range(1, k+1):
        w = item[i][0]
        v = item[i][1]

        if j < w:
            dp[i][j] = dp[i-1][j]
        else:
            dp[i][j] = max(dp[i-1][j], dp[i-1][j-w]+v)

print(dp[n][k])

💡결과

구글링을 해보니 1차원 배열로 푸는 분들도 계시던데 아직 동적 프로그래밍에 대해 익숙하지 않다보니 2차원 배열이 가시성이 좋아서 2차원으로 풀었는데,
역시나...메모리를 많이 잡아먹는거 같다.

코딩테스트에 자주 등장하는 단골이니 빨리 익숙해져야겠다🥲

동적 프로그래밍 공부 요약