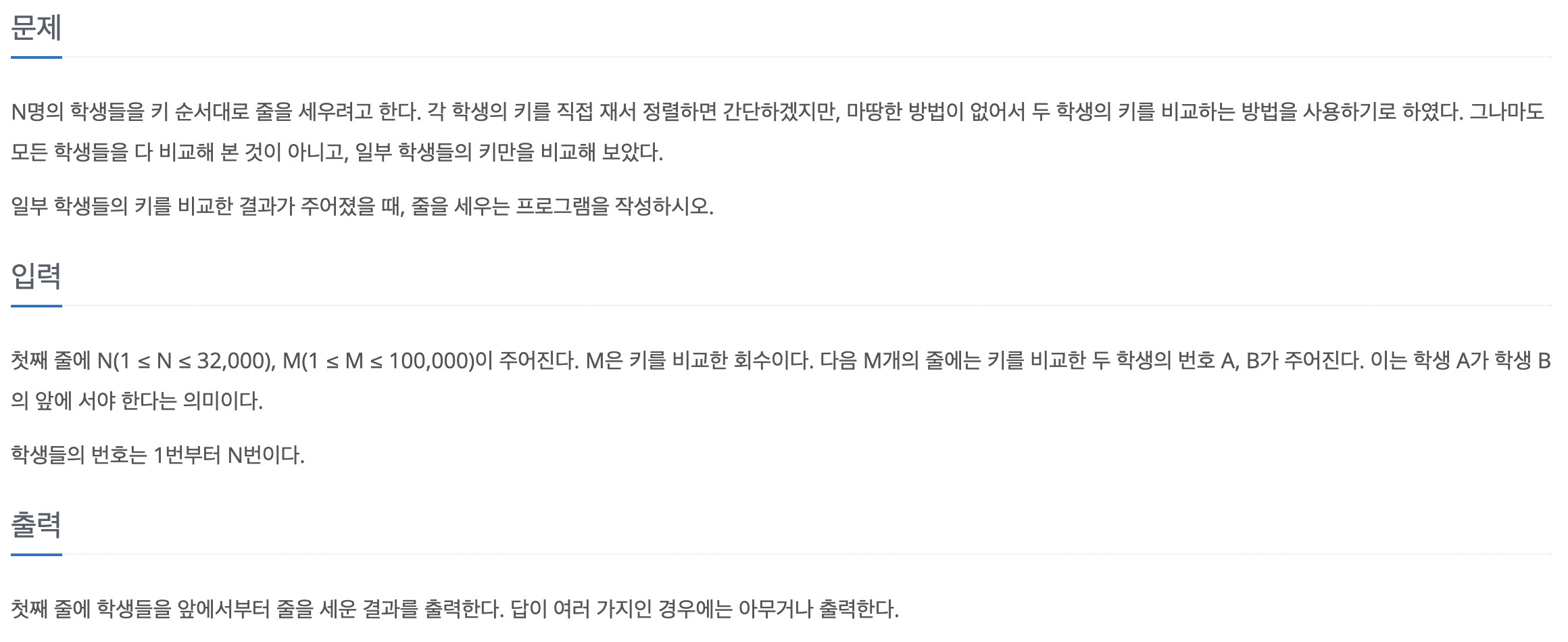
📖문제

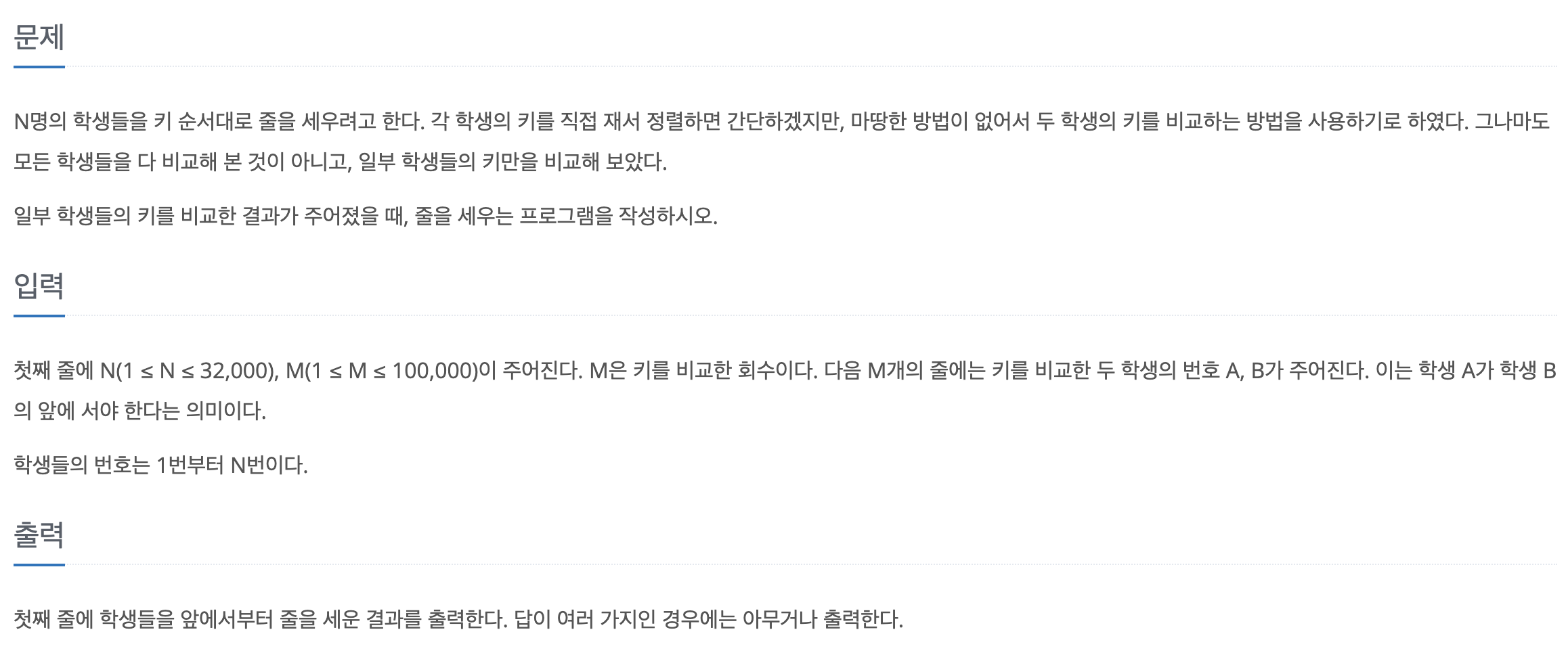
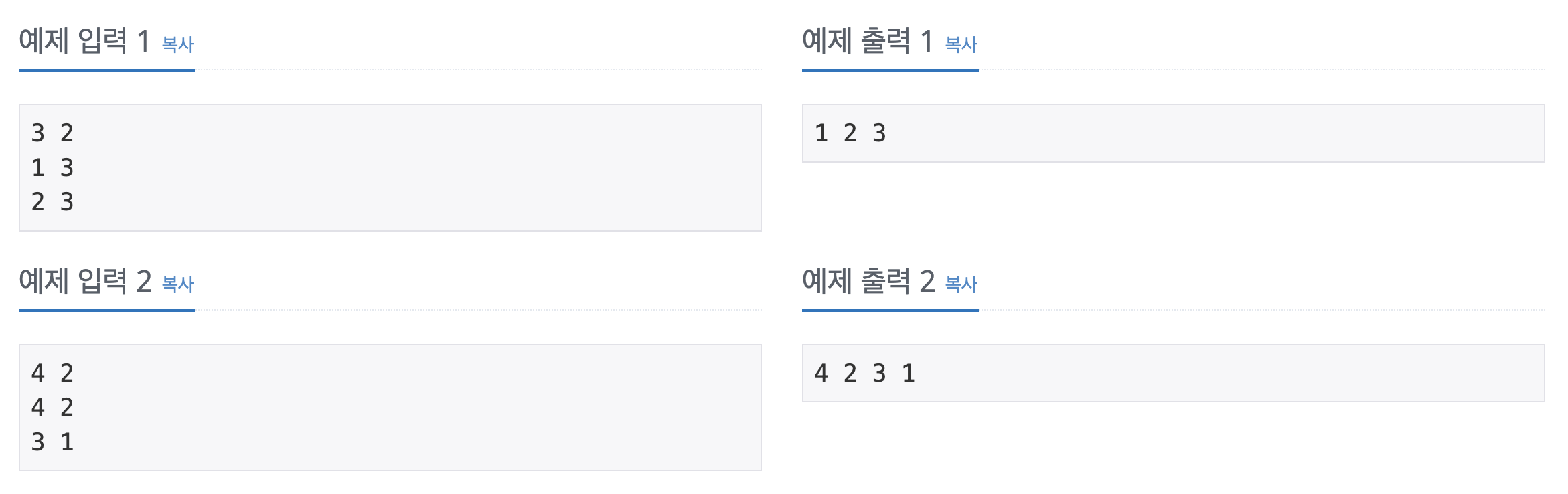
💡입&출력 예시

❓접근

알고리즘이 위상 정렬로 분류되어 있어 위상 정렬에 대해 알고 풀면 좋을 것이다.

🤔위상정렬이란?

위상정렬이란 순서가 정해져 있는 작업을 수행할 때 그 순서를 결정하기 위한 알고리즘을 말한다.

위상정렬을 적용하기 위한 조건은

DAG(Direted Acyclic Graph) 즉, 사이클이 발생하지 않는 방향그래프에만 적용이 가능하다.

DAG의 예시

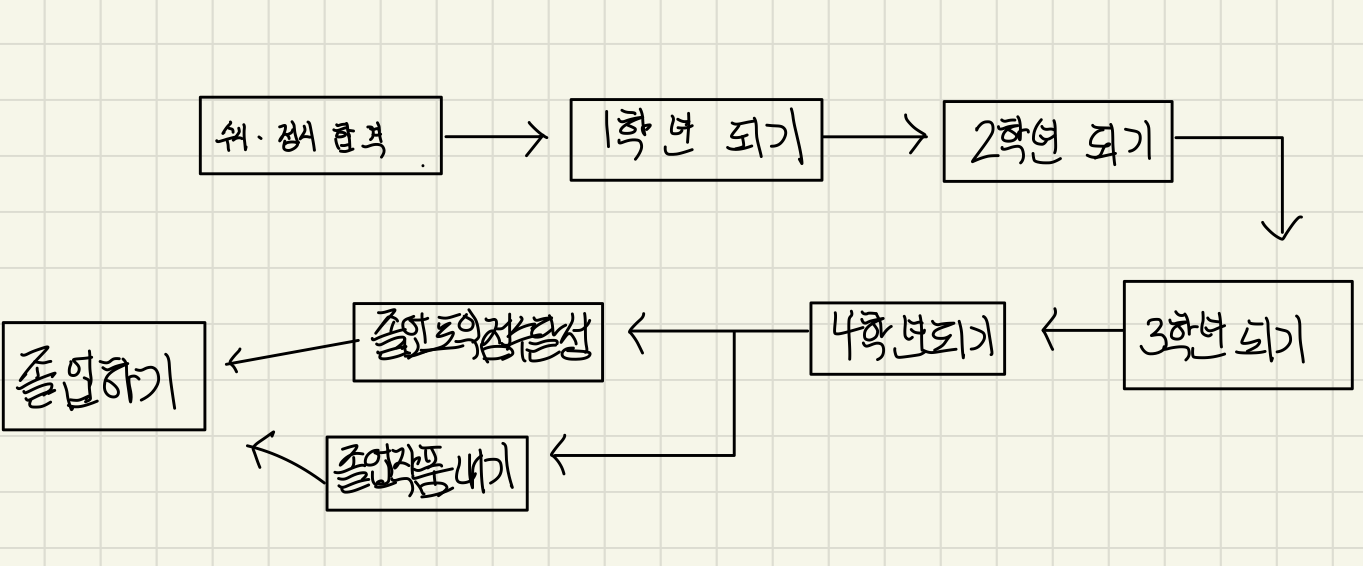
DAG가 아닌 예시

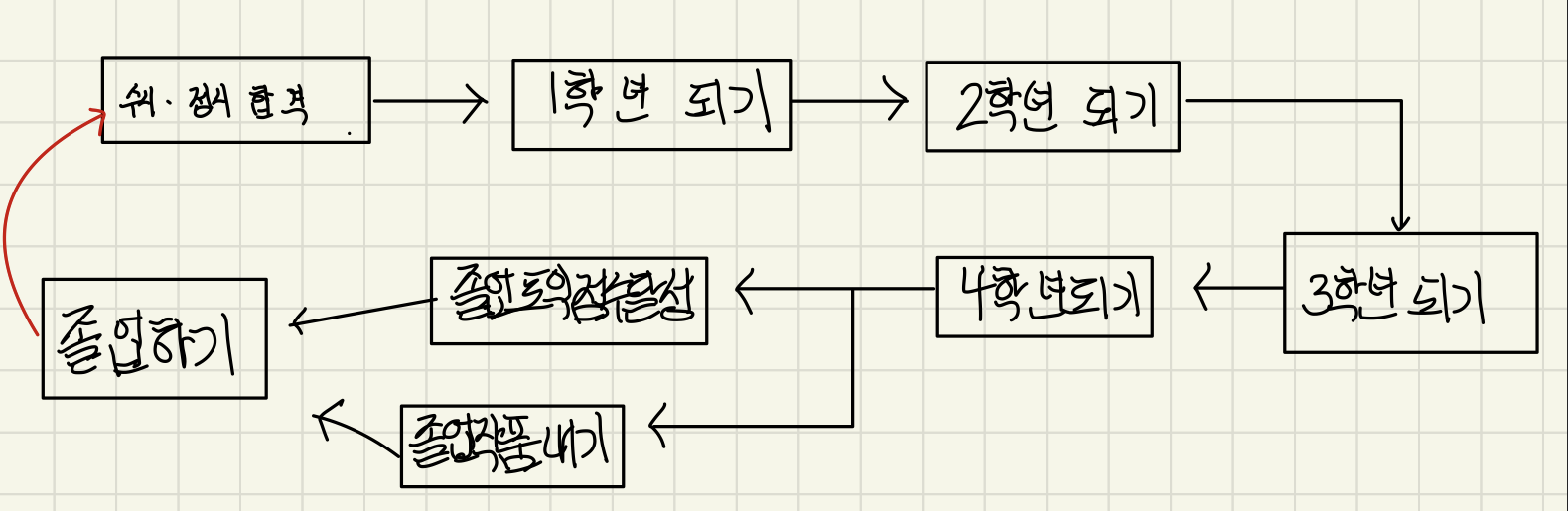
두번째 그림처럼 순환이 발생할 경우 위상정렬 알고리즘을 적용할 수 없다.

(물론 다시 수시 정시를 보고싶지도 않다🥕)

문제로 돌아가서 해당 문제는 위상정렬로 접근이 가능하다.

문제의 입력예시1을 보면
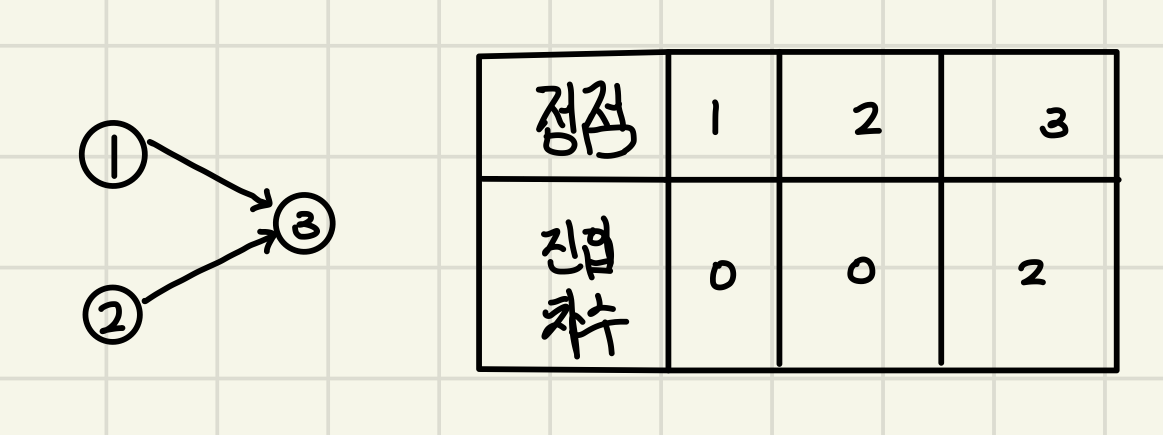
1번 학생 뒤에 3번학생, 2번학생 뒤에 3번학생이 서야 하므로 그래프는 다음과 같이 나타낼 수 있다.

사이클이 발생하지 않는 방향 그래프이기 때문에 위상 정렬로 구현 가능하다.

💡구현 방법

1. 진입차수 확인
2. 진입차수가 0인 정점을 큐에 삽입
3. 큐의 원소들을 꺼내 연결된 모든 간선 제거
4. 간선 제거 이후 진입차수가 0인 정점 큐에 삽입
5. 큐가 빌 때까지 2~4번 과정 반복
   (모든 원소를 방문했다면 큐에서 꺼낸 순서가 위상정렬의 결과)

진입차수 확인

입력예시 1을 기준으로 진입차수는 다음과 같다

🖥 코드

import sys
from collections import deque

ans = []
n,m = map(int, sys.stdin.readline().split())
queue = deque([])
degree = [0] * (n+1)
adj = [[] for _ in range(n+1)]

#1. 진입차수 확인
for _ in range(m):
  a,b = map(int, sys.stdin.readline().rstrip().split())
  adj[a].append(b)
  degree[b]+=1

#2.진입차수가 0인 정점을 큐에 삽입
for i in range(1, n+1):
  if(degree[i] == 0):
      queue.append(i)


while queue:
#3  큐의 원소들을 꺼내 연결된 모든 간선 제거
  temp = queue.popleft()
  ans.append(temp)
  for i in adj[temp]:
#4. 간선 제거 이후 진입차수가 0인 정점 큐에 삽입(반복)
      degree[i]-=1
      if degree[i] == 0 :
          queue.append(i)
#출력
print(*ans)

💡 백준 제출 결과

처음에 위상정렬이라는 개념을 모르고 문제를 풀다 보니 개념이 많이 생소했는데 다른 기술 블로그를 보며 개념을 익히는데 도움을 많이 받았습니다.

항상 열심히 배운다는 자세로 겸손하게 공부를 해야겠단 생각이 들었습니다.


참조:
안경잡이 개발자
hongcoding.tistory.com
동빈나 유투브