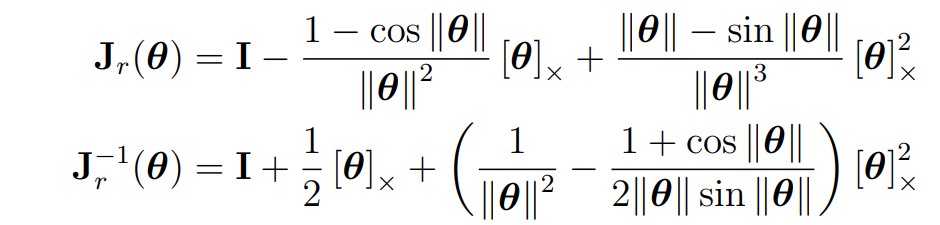참고자료 : Quaternion kinematics for the error-state Kalman filter
1. 쿼터니언의 정의 및 성질
쿼터니언은 a + b i a+bi a + b i q = q w + q x i + q y j + q z k ∈ H q = q_w + q_xi + q_yj + q_zk \in H q = q w + q x i + q y j + q z k ∈ H w h e r e { q w , q x , q y , q z } ∈ R a n d { i , j , k } i s i m a g i n a r y u n i t n u m b e r s where \space \{q_w, q_x, q_y, q_z\} \in R \space and \space \{i,j,k\} \space \space is \space imaginary \space unit \space numbers w h e r e { q w , q x , q y , q z } ∈ R a n d { i , j , k } i s i m a g i n a r y u n i t n u m b e r s
쿼터니언의 유용한 점 중 하나는 norm = 1인 unit quaternion을 이용해 3D 공간 상의 회전을 기술할 수 있다는 것이다. 이는 unit complex number을 이용해 2D rotation을 기술하는 것을 확장한 것으로 보면 편하다.
unit quaternion : q u = e ( u x i + u y j + u z k ) θ / 2 q_u=e^{(u_xi+u_yj+u_zk)\theta/2} q u = e ( u x i + u y j + u z k ) θ / 2 x ′ = q u ⊗ x ⊗ q u ∗ x'=q_u\otimes x \otimes q_u^* x ′ = q u ⊗ x ⊗ q u ∗
general quaternion : q = q w + q v = [ q w q v ] = [ q w q x q y q z ] q=q_w + q_v = \begin{bmatrix}q_w\\q_v\end{bmatrix}=\begin{bmatrix}q_w\\q_x\\q_y\\q_z\end{bmatrix} q = q w + q v = [ q w q v ] = ⎣ ⎢ ⎢ ⎢ ⎡ q w q x q y q z ⎦ ⎥ ⎥ ⎥ ⎤
real quaternion : q w = [ q w 0 ] q_w=\begin{bmatrix}q_w\\0\end{bmatrix} q w = [ q w 0 ]
pure quaternion : q v = [ 0 q v ] q_v=\begin{bmatrix}0\\q_v\end{bmatrix} q v = [ 0 q v ]
quaternion sum : p + q = [ p w ± q w p v ± q v ] p+q=\begin{bmatrix}p_w\pm q_w\\p_v \pm q_v\end{bmatrix} p + q = [ p w ± q w p v ± q v ]
quaternion product p ⊗ q = [ p w q w − p v T q v p w q v + q w p v + p v × q v ] p\otimes q=\begin{bmatrix}p_wq_w-p_v^Tq_v\\p_wq_v+q_wp_v+p_v\times q_v\end{bmatrix} p ⊗ q = [ p w q w − p v T q v p w q v + q w p v + p v × q v ]
quaternion product를 행렬 연산으로 대체하기 위해 left/right quaternion product matrix를 정의할 수 있다.q 1 ⊗ q 2 = [ q 1 ] L q 2 = [ q 2 ] R q 1 q_1\otimes q_2=[q_1]_Lq_2=[q_2]_Rq_1 q 1 ⊗ q 2 = [ q 1 ] L q 2 = [ q 2 ] R q 1
[ q ] L = q w I 4 + [ 0 3 − q v T q v [ q v ] × ] [q]_L=q_wI_4+\begin{bmatrix}0_3&-q_v^T\\q_v&[q_v]_\times\end{bmatrix} [ q ] L = q w I 4 + [ 0 3 q v − q v T [ q v ] × ]
[ q ] R = q w I 4 + [ 0 3 − q v T q v − [ q v ] × ] [q]_R=q_wI_4+\begin{bmatrix}0_3&-q_v^T\\q_v&-[q_v]_\times\end{bmatrix} [ q ] R = q w I 4 + [ 0 3 q v − q v T − [ q v ] × ]
skew operator : [ w ] × = [ 0 − w z w y w z 0 − w x − w y w x 0 ] , [ a ] × b = a × b [w]_\times=\begin{bmatrix}0&-w_z&w_y\\w_z&0&-w_x\\-w_y&w_x&0\end{bmatrix}, \quad [a]_\times b=a\times b [ w ] × = ⎣ ⎢ ⎡ 0 w z − w y − w z 0 w x w y − w x 0 ⎦ ⎥ ⎤ , [ a ] × b = a × b
identity quaternion : q 1 = 1 = [ 1 0 v ] q_1=1=\begin{bmatrix}1\\0_v\end{bmatrix} q 1 = 1 = [ 1 0 v ]
conjugate of quaternion : q ∗ = q w − q v = [ q w − q v ] q^*=q_w-q_v=\begin{bmatrix}q_w\\-q_v\end{bmatrix} q ∗ = q w − q v = [ q w − q v ]
norm of quaternion : ∣ ∣ q ∣ ∣ = q ⊗ q ∗ = q w 2 + q x 2 + q y 2 + q z 2 ||q||=\sqrt{q\otimes q^*}=\sqrt{q_w^2+q_x^2+q_y^2+q_z^2} ∣ ∣ q ∣ ∣ = q ⊗ q ∗ = q w 2 + q x 2 + q y 2 + q z 2
inverse of quaternion : q − 1 = q ∗ / ∣ ∣ q ∣ ∣ 2 , q ⊗ q ∗ = q ∗ ⊗ q = q 1 q^{-1}=q^*/||q||^2,\quad q\otimes q^*=q^* \otimes q=q_1 q − 1 = q ∗ / ∣ ∣ q ∣ ∣ 2 , q ⊗ q ∗ = q ∗ ⊗ q = q 1
unit quaternion : ∣ ∣ q ∣ ∣ = 1 , q − 1 = q ∗ , q = [ c o s θ u ∗ s i n θ ] ||q||=1, \space q^{-1}=q^*,\space q=\begin{bmatrix}cos\theta\\u*sin\theta\end{bmatrix} ∣ ∣ q ∣ ∣ = 1 , q − 1 = q ∗ , q = [ c o s θ u ∗ s i n θ ]
exponential of pure quaternion v = v x i + v y j + v z k v=v_xi+v_yj+v_zk v = v x i + v y j + v z k e v = e u θ = [ c o s θ u ∗ s i n θ ] e^v=e^{u\theta}=\begin{bmatrix}cos\theta\\u*sin\theta\end{bmatrix} e v = e u θ = [ c o s θ u ∗ s i n θ ]
exponential of general quaternion e q = e q w e q v = e q w e u θ e^q=e^{q_w}e^{q_v}=e^{q_w}e^{u\theta} e q = e q w e q v = e q w e u θ e q = e w q [ c o s ∣ ∣ q v ∣ ∣ q v ∣ ∣ q v ∣ ∣ s i n ∣ ∣ q v ∣ ∣ ] e^q=e^q_w\begin{bmatrix}cos||q_v||\\\frac{q_v}{||q_v||}sin||q_v||\end{bmatrix} e q = e w q [ c o s ∣ ∣ q v ∣ ∣ ∣ ∣ q v ∣ ∣ q v s i n ∣ ∣ q v ∣ ∣ ]
logarithm of unit quaternion l o g q = l o g ( c o s θ + u s i n θ ) = l o g ( e u θ ) = u θ log\space q=log(cos\theta+u\space sin\theta)=log(e^{u\theta})=u\space \theta l o g q = l o g ( c o s θ + u s i n θ ) = l o g ( e u θ ) = u θ u = q v ∥ ∣ q v ∣ ∣ u=q_v\||q_v|| u = q v ∥ ∣ q v ∣ ∣ θ = a r c t a n ( ∣ ∣ q v ∣ ∣ , q w ) \theta=arctan(||q_v||,q_w) θ = a r c t a n ( ∣ ∣ q v ∣ ∣ , q w )
logarithm of general quaternion l o g q = l o g ∣ ∣ q ∣ ∣ + u θ = [ l o g ∣ ∣ q ∣ ∣ u θ ] log\space q=log||q||+u\theta=\begin{bmatrix}log||q||\\u\theta\end{bmatrix} l o g q = l o g ∣ ∣ q ∣ ∣ + u θ = [ l o g ∣ ∣ q ∣ ∣ u θ ]
unit quaternion의 거듭제곱 : q t = e x p ( t u θ ) = [ c o s ( t θ ) u s i n ( t θ ) ] q^t=exp(t\space u\space \theta)=\begin{bmatrix}cos(t\theta)\\u\space sin(t\theta)\end{bmatrix} q t = e x p ( t u θ ) = [ c o s ( t θ ) u s i n ( t θ ) ]
2. rotation과의 상호 관계
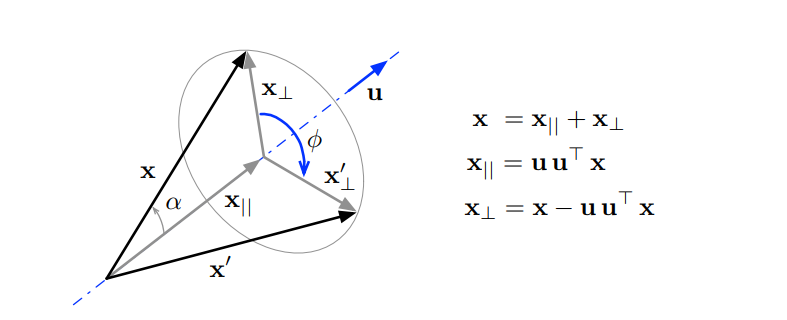
vector x x x u u u ϕ \phi ϕ x x x u u u x = x ∥ + x ⊥ x=x_{\parallel}+x_{\bot} x = x ∥ + x ⊥ x ∥ = u u T x , x ⊥ = x − u u T x x_{\parallel}=uu^Tx,\quad x_{\bot}=x-uu^Tx x ∥ = u u T x , x ⊥ = x − u u T x
x ′ = x ∥ + x ⊥ c o s ϕ + ( u × x ) s i n ϕ x'=x_{\parallel}+x_{\bot}cos\phi+(u\times x)sin\phi x ′ = x ∥ + x ⊥ c o s ϕ + ( u × x ) s i n ϕ
exponential map of rotation matrix R = E x p ( ϕ ) = e x p ( [ ϕ ] × ) R=Exp(\phi)=exp([\phi]_{\times}) R = E x p ( ϕ ) = e x p ( [ ϕ ] × )
여기서 vector ϕ ∈ R 3 \phi \in R^3 ϕ ∈ R 3 ϕ ∈ R \phi \in R ϕ ∈ R u u u
Rodrigues rotation formula R = e [ ϕ ] × = e ϕ [ u ] × = I 3 c o s ϕ + [ u ] × s i n ϕ + u u T ( 1 − c o s ϕ ) R=e^{[\phi]_{\times}}=e^{\phi[u]_{\times}}=I_3cos\phi+[u]_{\times}sin\phi+uu^T(1-cos\phi) R = e [ ϕ ] × = e ϕ [ u ] × = I 3 c o s ϕ + [ u ] × s i n ϕ + u u T ( 1 − c o s ϕ )
logarithmic map of rotation matrix l o g ( R ) = ϕ [ u ] × log(R)=\phi[u]_{\times} l o g ( R ) = ϕ [ u ] × ϕ = a r c c o s ( t r ( R ) − 1 2 ) , u = ( R − R T ) ∨ 2 s i n ϕ \phi=arccos(\frac{tr(R)-1}{2}),\quad u=\frac{(R-R^T)^{\vee}}{2sin\phi} ϕ = a r c c o s ( 2 t r ( R ) − 1 ) , u = 2 s i n ϕ ( R − R T ) ∨
L o g ( R ) = u ϕ Log(R)=u\phi L o g ( R ) = u ϕ
rotation using rotation matrix x ′ = R x = E x p ( u ϕ ) x = x ∥ + ( u × x ) s i n ϕ + x ⊥ c o s ϕ x'=Rx=Exp(u\phi)\space x=x_{\parallel}+(u\times x)sin\phi+x_{\bot}cos\phi x ′ = R x = E x p ( u ϕ ) x = x ∥ + ( u × x ) s i n ϕ + x ⊥ c o s ϕ
exponential map V ∈ H p V \in H_p V ∈ H p e x p ( V ) = e V exp(V)=e^V e x p ( V ) = e V
rotation vector ϕ ∈ R 3 \phi \in R^3 ϕ ∈ R 3 R 3 R^3 R 3 E x p ( ϕ ) = e x p ( ϕ / 2 ) = e ϕ / 2 Exp(\phi)=exp(\phi/2)=e^{\phi/2} E x p ( ϕ ) = e x p ( ϕ / 2 ) = e ϕ / 2
이로부터 rotation벡터에 대응되는 unit quaternion을 얻을 수 있다.q = E x p ( ϕ u ) = e ϕ u / 2 = [ c o s ( ϕ / 2 ) u s i n ( ϕ / 2 ) ] q=Exp(\phi u)=e^{\phi u/2}=\begin{bmatrix}cos(\phi/2)\\u\space sin(\phi/2)\end{bmatrix} q = E x p ( ϕ u ) = e ϕ u / 2 = [ c o s ( ϕ / 2 ) u s i n ( ϕ / 2 ) ]
logarithmic map l o g ( q ) = u θ = u ϕ / 2 log(q)=u\theta=u\phi/2 l o g ( q ) = u θ = u ϕ / 2
L o g ( q ) = u ϕ Log(q)=u\phi L o g ( q ) = u ϕ
unit quaternion으로부터 angle-axis 값을 아래와 같이 얻을 수 있다.
ϕ = 2 a r c t a n ( ∣ ∣ q v ∣ ∣ , q w ) \phi=2arctan(||q_v||, q_w) ϕ = 2 a r c t a n ( ∣ ∣ q v ∣ ∣ , q w ) u = q v / ∣ ∣ q v ∣ ∣ u=q_v/||q_v|| u = q v / ∣ ∣ q v ∣ ∣
rotation using quaternion
r ( x ) = q ⊗ x ⊗ q ∗ = x ∥ + ( u × x ) s i n ϕ + x ⊥ c o s ϕ r(x)=q\otimes x\otimes q^*=x_{\parallel}+(u\times x)sin\phi+x_{\bot}cos\phi r ( x ) = q ⊗ x ⊗ q ∗ = x ∥ + ( u × x ) s i n ϕ + x ⊥ c o s ϕ
2.5. rotation matrix와 quaternion
ϕ , x ∈ R 3 , q = E x p ( ϕ ) , R = E x p ( ϕ ) \phi,x \in R^3, \quad q=Exp(\phi), \quad R=Exp(\phi) ϕ , x ∈ R 3 , q = E x p ( ϕ ) , R = E x p ( ϕ ) q ⊗ x ⊗ q ∗ = R x q\otimes x \otimes q^*=Rx q ⊗ x ⊗ q ∗ = R x
R = ( q w 2 − q v T q v ) I 3 + 2 q v q v T + 2 q w [ q v ] × R=(q_w^2-q_v^Tq_v)I_3+2q_vq_v^T+2q_w[q_v]_\times R = ( q w 2 − q v T q v ) I 3 + 2 q v q v T + 2 q w [ q v ] ×
2.6. rotation composition
q A C = q A B ⊗ q B C , R A C = R A B R B C q_{AC}=q_{AB}\otimes q_{BC}, \quad R_{AC}=R_{AB}R_{BC} q A C = q A B ⊗ q B C , R A C = R A B R B C
3. 쿼터니언 컨벤션
쿼터니언을 표현하는 2가지 컨벤션이 존재한다.
Hamilton type : q = ( q w , q v ) q=(q_w,q_v) q = ( q w , q v ) q = ( q v , q w ) q=(q_v,q_w) q = ( q v , q w )
C++ Eigen library의 경우 Hamilton type(w, x, y, z 순서)을 사용한다.
또한 q.coeffs() 메서드를 사용해서 값을 받아왔을 때도 JPL type(x, y, z, w 순서)으로 값이 저장되어있다.
여기서는 Hamilton 타입을 사용한다.
Active vs Passive x ′ = q a c t i v e ⊗ x ⊗ q a c t i v e ∗ x'=q_{active}\otimes x \otimes q_{active}^* x ′ = q a c t i v e ⊗ x ⊗ q a c t i v e ∗ x ′ = R a c t i v e x x'=R_{active}x x ′ = R a c t i v e x
Passive interpretation : vector는 그대로이고, 좌표계가 회전. frame transformation.x B = q p a s s i v e ⊗ x A ⊗ q p a s s i v e ∗ x_B=q_{passive} \otimes x_{A} \otimes q_{passive}^* x B = q p a s s i v e ⊗ x A ⊗ q p a s s i v e ∗ x B = R p a s s i v e x A x_{B}=R_{passive}x_{A} x B = R p a s s i v e x A
A , B A, B A , B x A , x B x_{A},x_{B} x A , x B x x x
아래와 같은 관계를 가진다.q a c t i v e = q p a s s i v e ∗ q_{active}=q_{passive}^* q a c t i v e = q p a s s i v e ∗ R a c t i v e = R p a s s i v e T R_{active}=R_{passive}^T R a c t i v e = R p a s s i v e T
4. Perturbation / Derivative / Integral
4.1. additive, subtractive operators in SO3
q S = q R ⊕ θ = q R ⊗ E x p ( θ ) q_S=q_R \oplus \theta=q_R \otimes Exp(\theta) q S = q R ⊕ θ = q R ⊗ E x p ( θ ) R S = R R ⊕ θ = R R E x p ( θ ) R_S=R_R \oplus \theta=R_R Exp(\theta) R S = R R ⊕ θ = R R E x p ( θ )
θ = q S ⊖ q R = L o g ( q R ∗ ⊗ q S ) \theta=q_S \ominus q_R=Log(q_R^* \otimes q_S) θ = q S ⊖ q R = L o g ( q R ∗ ⊗ q S ) θ = R S ⊖ R R = L o g ( R R T R S ) \theta=R_S \ominus R_R=Log(R_R^TR_S) θ = R S ⊖ R R = L o g ( R R T R S )
4.3. Jacobians of the rotation
Jacobian respect to vector
∂ ( q ⊗ a ⊗ q ∗ ) ∂ a = ∂ ( R a ) ∂ a = R \frac{\partial(q\otimes a \otimes q^*)}{\partial a}=\frac{\partial (Ra)}{\partial a}=R ∂ a ∂ ( q ⊗ a ⊗ q ∗ ) = ∂ a ∂ ( R a ) = R
Jacobian respect to quaternion
∂ ( q ⊗ a ⊗ q ∗ ) ∂ q = 2 [ w a + v × a ∣ v T a I 3 + v a T − a v T − w [ a ] × ] ∈ R 3 × 4 \frac{\partial(q \otimes a \otimes q^*)}{\partial q}=2[wa+v\times a | v^TaI_3+va^T-av^T-w[a]_\times] \in R^{3\times 4} ∂ q ∂ ( q ⊗ a ⊗ q ∗ ) = 2 [ w a + v × a ∣ v T a I 3 + v a T − a v T − w [ a ] × ] ∈ R 3 × 4
Right Jacobian of SO(3)
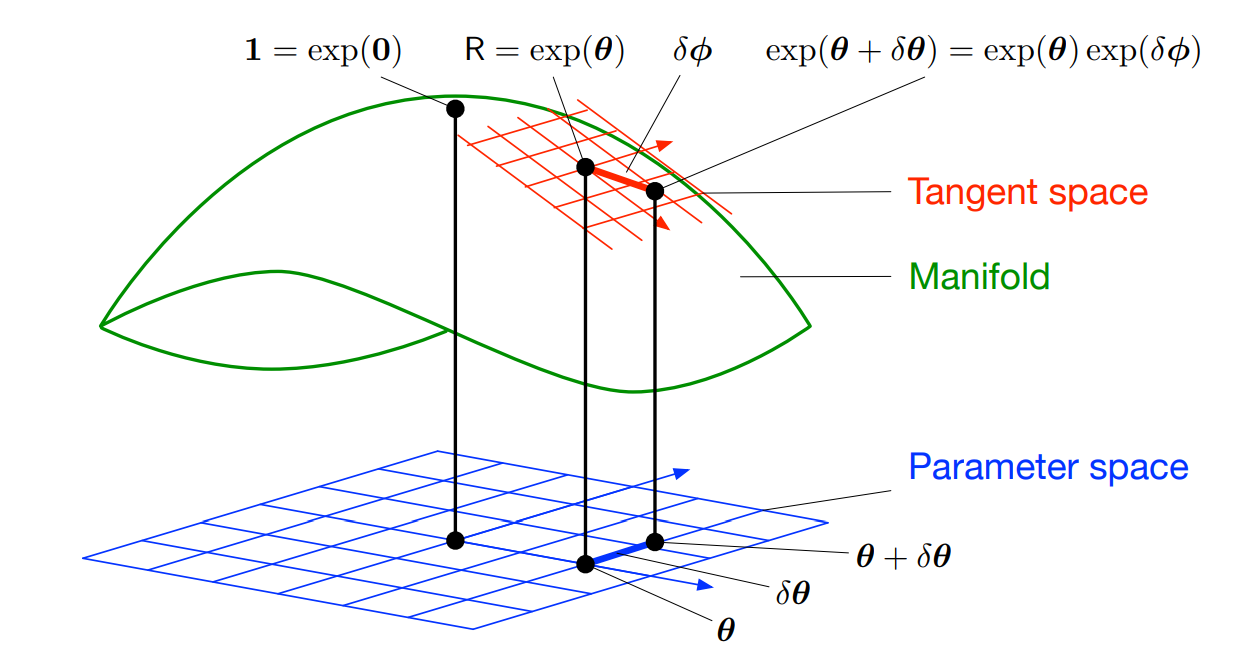
rotation vector θ ∈ R 3 \theta \in R^3 θ ∈ R 3 δ θ \delta \theta δ θ δ ϕ ∈ R 3 \delta \phi \in R^3 δ ϕ ∈ R 3
E x p ( θ ) ⊗ δ ϕ = E x p ( θ + δ θ ) Exp(\theta) \otimes \delta \phi=Exp(\theta+\delta \theta) E x p ( θ ) ⊗ δ ϕ = E x p ( θ + δ θ )
δ ϕ = L o g ( E x p ( θ ) − 1 ∘ E x p ( θ + δ θ ) ) = E x p ( θ + δ θ ) ⊖ E x p ( θ ) \delta \phi =Log(Exp(\theta)^{-1} \circ Exp(\theta+\delta \theta))=Exp(\theta+\delta \theta) \ominus Exp(\theta) δ ϕ = L o g ( E x p ( θ ) − 1 ∘ E x p ( θ + δ θ ) ) = E x p ( θ + δ θ ) ⊖ E x p ( θ )
Right Jacobian : J r = ∂ δ ϕ ∂ δ θ = ∂ E x p ( θ ) ∂ θ J_r=\frac{\partial \delta \phi}{\partial \delta \theta}=\frac{\partial Exp(\theta)}{\partial \theta} J r = ∂ δ θ ∂ δ ϕ = ∂ θ ∂ E x p ( θ )
Right Jacobian의 closed form은 아래와 같다.
Right Jacobian은 아래와 같은 특성을 가진다.E x p ( θ + δ θ ) ≈ E x p ( θ ) E x p ( J r ( θ ) δ θ ) Exp(\theta+\delta \theta) \approx Exp(\theta)Exp(J_r(\theta)\delta \theta) E x p ( θ + δ θ ) ≈ E x p ( θ ) E x p ( J r ( θ ) δ θ ) E x p ( θ ) E x p ( δ θ ) ≈ E x p ( θ + J r − 1 ( θ ) δ θ ) Exp(\theta)Exp(\delta \theta) \approx Exp(\theta+J_r^{-1}(\theta)\delta \theta) E x p ( θ ) E x p ( δ θ ) ≈ E x p ( θ + J r − 1 ( θ ) δ θ ) L o g ( E x p ( θ ) E x p ( δ θ ) ) ≈ θ + J r − 1 ( θ ) δ θ Log(Exp(\theta)Exp(\delta \theta)) \approx \theta + J_r^{-1}(\theta)\delta \theta L o g ( E x p ( θ ) E x p ( δ θ ) ) ≈ θ + J r − 1 ( θ ) δ θ
Jacobian respect to rotation vector ∂ ( q ⊗ a ⊗ q ∗ ) ∂ δ θ = ∂ ( R a ) ∂ δ θ = − R θ [ a ] × J r ( θ ) \frac{\partial (q \otimes a \otimes q^*)}{\partial \delta \theta}=\frac{\partial (Ra)}{\partial \delta \theta}=-R{\theta}[a]_\times J_r(\theta) ∂ δ θ ∂ ( q ⊗ a ⊗ q ∗ ) = ∂ δ θ ∂ ( R a ) = − R θ [ a ] × J r ( θ )
4.4 Perturbation / Uncertainty / Noise
local perturbation q ~ = q ⊗ Δ q L \tilde{q}=q \otimes \Delta q_{L} q ~ = q ⊗ Δ q L R ~ = R Δ R L \tilde{R}=R \Delta R_L R ~ = R Δ R L
local perturbation을 rotation vector form으로 표현하면,
q L ~ = q L ⊗ E x p ( Δ ϕ L ) \tilde{q_L}=q_L \otimes Exp(\Delta\phi_L) q L ~ = q L ⊗ E x p ( Δ ϕ L ) R L ~ = R L E x p ( Δ ϕ L ) \tilde{R_L}=R_L Exp(\Delta \phi_L) R L ~ = R L E x p ( Δ ϕ L )
Δ ϕ L = L o g ( q L ∗ ⊗ q L ~ ) = L o g ( R L T R ~ L ) \Delta \phi_L=Log(q_L^* \otimes \tilde{q_L})=Log(R_L^T\tilde{R}_L) Δ ϕ L = L o g ( q L ∗ ⊗ q L ~ ) = L o g ( R L T R ~ L )
perturbation angle이 작은 경우 perturbation의 quaternion / rotation matrix form은 아래와 같이 근사할 수 있다.
Δ q L ≈ [ 1 1 2 Δ ϕ L ] \Delta q_L \approx \begin{bmatrix} 1 \\ \frac{1}{2}\Delta\phi_L \end{bmatrix} Δ q L ≈ [ 1 2 1 Δ ϕ L ] Δ R L ≈ I + [ Δ ϕ L ] × \Delta R_L \approx I + [\Delta\phi_L]_\times Δ R L ≈ I + [ Δ ϕ L ] ×
global perturbation
q ~ G = E x p ( Δ ϕ G ) ⊗ q G \tilde{q}_G=Exp(\Delta\phi_G)\otimes q_G q ~ G = E x p ( Δ ϕ G ) ⊗ q G R ~ G = E x p ( Δ ϕ G ) R G \tilde{R}_G=Exp(\Delta\phi_G)R_G R ~ G = E x p ( Δ ϕ G ) R G
Δ ϕ G = L o g ( q ~ G ⊗ q G ∗ ) = L o g ( R ~ G R G T ) \Delta\phi_G=Log(\tilde{q}_G\otimes q_G^*)=Log(\tilde{R}_GR^T_G) Δ ϕ G = L o g ( q ~ G ⊗ q G ∗ ) = L o g ( R ~ G R G T )
4.5. Time derivatives
w L ( t ) = d ϕ L ( t ) d t w_L(t)=\frac{d\phi_L(t)}{dt} w L ( t ) = d t d ϕ L ( t )
q ˙ = lim Δ t → 0 q ( t + Δ t ) − q ( t ) Δ t = 1 2 q ⊗ [ 0 w L ] \dot{q}=\lim\limits_{\Delta t \to 0}\frac{q(t+\Delta t)-q(t)}{\Delta t}=\frac{1}{2}q \otimes \begin{bmatrix}0 \\ w_L\end{bmatrix} q ˙ = Δ t → 0 lim Δ t q ( t + Δ t ) − q ( t ) = 2 1 q ⊗ [ 0 w L ]
q ˙ = 1 2 [ w L ] R ∗ q = 1 2 q ⊗ w L \dot{q}=\frac{1}{2}[w_L]_R*q=\frac{1}{2}q\otimes w_L q ˙ = 2 1 [ w L ] R ∗ q = 2 1 q ⊗ w L
R ˙ = R [ w L ] × \dot{R}=R[w_L]_\times R ˙ = R [ w L ] ×
global perturbation을 사용하면
q ˙ = 1 2 w G ⊗ q \dot{q}=\frac{1}{2}w_G\otimes q q ˙ = 2 1 w G ⊗ q
R ˙ = [ w G ] × R \dot{R}=[w_G]_\times R R ˙ = [ w G ] × R
4.6. Time integral of rotation rate(angular velocity)
angular velocity 가 변하지 않는다고 가정하면q n + 1 = q n ⊗ q { w n Δ t } q_{n+1}=q_n \otimes q\{w_n \Delta t\} q n + 1 = q n ⊗ q { w n Δ t }