내적
내적을 사용하는 이유
내적을 사용하면 여러가지를 할 수 있겠지만 근본적으로 두 벡터 사이의 사잇각을 구할 수 있다. 이렇게 되면 게임 개발을 할 때 시야각이나 회전각등 여러가지 기능 분야에서 사용할 수 있다. 이러한 내적을 활용하는 것이 게임 수학의 기본이며 내적을 할 줄 알아야 게임 수학을 어느정도 다룰 줄 안다고 할 수 있다.
내적 없어도 게임 개발 충분히 되는데? 그걸 왜 배워야 돼?
사실 저자는 유니티 개발을 하면서 내적을 사용한 경우는 많이 있는 것 같지는 않다. 내적을 사용하지 않고도 어느정도 개발이 가능하기 때문이다. 정확히 말하자면 내적을 활용해서 만든 내부 유니티 함수가 많기 때문이다.
ex)
Vector3 vec;
vec.magnitude;하지만 게임개발자가 내부적으로 돌아가는 방식도 모르고 이러한 함수를 사용하는 것은 옳지 않다고 말할 수 있다. 오류가 나도 어디서 오류가 나는지 알기 힘들며, 내적을 이용해 사용해야하는 다른 함수를 정의해야하는 경우가 생길 수 있기 때문에 알고 있어야 한다.
내적의 정의
내적은 두 벡터의 곱이다. 벡터값을 마치 수처럼 곱하는 것이다.
벡터에는 방향이 있으므로 방향이 일치하는 만큼 곱한다.
벡터는 스칼라 즉 방향이 없는 실수 값이 나오게된다.
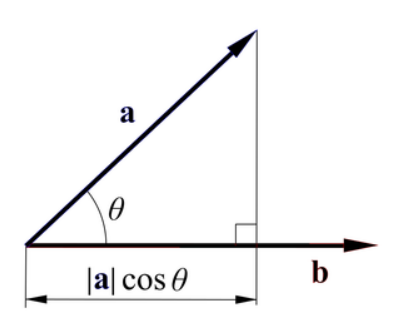
아래 식은 벡터의 공식이다.
절대값이 씌워진 a 와 b 벡터는 길이를 의미하며 cosθ에 있는 θ는 두 벡터의 사잇각을 의미한다.
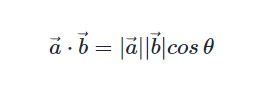
벡터를 구하는 방법은 x값과 y값을 곱해서 더하는 공식이 있다.
(x1,y1) • (x2,y2) 를 구하게 되면은 (x1 곱하기 x2) + (y1 곱하기 y2) 방식으로 구하면 된다.
ex)
(2,3) • (4,5) = 2*3 + 4*5 = 26이러한 방식으로 구하면 된다.
내적의 활용
이 식을 다시 가져와보자
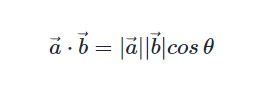
여기서 우리가 중요하게 여길 것이 있다. a벡터길이와 b벡터 길이가 곱해서 1이 되면 cosθ만 남게 된다. 이렇게 되면은 역 Cos함수에다 Cosθ를 넣게 되면은 θ값, 즉 사잇값을 구할 수 있게 된다.
아래는 유니티를 활용한 두 벡터의 내적 예시 코드이다.
ex)
Vector2 firstVec;
Vector2 secondVec;
float viewAngle = 30f;
firstVec.Normalize();
secondVec.Normalize();
float value = (firstVec.x * secondVec.x + secondVec.y * second.y);
float currentAngle = Acos(vlaue) * Mathf.Rad2Deg;
if(currentAngle < viewAngel)
{
return true;
}
아래 예시 코드는 두 벡터를 Normalize 정규화 하여, cosθ값을 구할 수 있다. 여기서 역Cos함수에 넣어주게되면 벌어진 정도를 구하고 만약 정해진 값보다 작으면 true를 리턴해주는 함수이다 시야각 함수를 구할 때 사용하는 방법이다.
느낀점
정말로 상용화 엔진을 사용하는 것이 이런 세세한 기능까지 다 구현되어있다는 것이 너무 편한 것 같다. 게임수학을 더 배워서 프로젝트를 할 때 활용하거나 유니티 내부 구현 함수를 사용할 때 내부적으로 어떻게 돌아가는지 계산하면서 활용하면은 게임개발을 할 때 좀 더 전문적인 개발을 할 수 있지 않을까 생각했다.
-추후에 투영벡터 내용 추가 예정-
