◉ 학습목표
1. Tree 자료구조를 이해하고 구현해낼 수 있다.
2. Graph 자료구조를 이해하고 구현해낼 수 있다.
3. BST(Binary Search Tree) 자료구조를 이해하고 구현해낼 수 있다.
- Tree (트리)
⦿ 학습내용
☞ Tree(트리) 구조
✔︎ 단방향 그래프, 하나의 뿌리에서 가지가 사방으로 뻗은 형태
✔︎ 데이터가 바로 아래 하나 이상의 데이터에 무방향으로 연결된 계층구조
✔︎ 데이터를 순차적으로 나열된 선형 구조가 아니라, 하나의 데이터 아래 여러 개의 데이터가 존재할 수 있는 비선형 구조
✔︎ 아래로만 뻗기 때문에 사이클 존재 ❌
☞ Tree 용어 정리
✔︎ 노드(Node) : 트리 구조를 이루는 모든 개별 데이터
✔︎ 루트(Root) : 트리 구조의 시작점이 되는 노드
✔︎ 부모 노드(Parent node) : 두 노드가 상하관계로 연결되어 있을 때, 상대적으로 루트에서 가까운 노드
✔︎ 자식 노드(Child node) : 두 노드가 상하관계에 연결되어 있을 때, 상대적으로 루트에서 먼 노드
✔︎ 리프(Leaf) : 트리 구조의 끝 지점, 자식 노드가 없는 노드
✔︎ 깊이(depth) : 루트 노드부터 하위 특정 노드까지의 깊이, 루트부터 깊이는 0
✔︎ 레벨(level) : 같은 깊이를 가지고 있는 노드를 묶어서 레벨, 루트부터 레벨은 1
✔︎ 높이(height) : 리프 노드 기준으로 루트 노드까지의 높이, 리프부터 높이 0
✔︎ 서브 트리(sub tree) : 루트부터 뻗어나오는 트리 내부에 트리 구조를 가진 작은 트리
- Graph (그래프)
⦿ 학습내용
☞ Graph(그래프) 구조
✔︎ 여러 개의 점들이 서로 복잡하게 연결되어 있는 관계를 표현한 자료구조
✔︎ 직접적인 관계 : 두 점 사이를 연결해주는 선이 있음
✔︎ 간접적인 관계 : 몇 개의 점과 선에 걸쳐 이어짐
✔︎ 인접 행렬 : 서로 다른 정점들이 인접한지 표현한 2차원 배열 형태의 행렬
✔︎ 인접 리스트 : 각 정점이 어떤 정점과 인접한지 리스트 형태로 표현
☞ Graph 용어 정리
✔︎ 정점(vertex) : 노드라고도 함, 데이터가 저장되는 그래프의 기본 원소
✔︎ 간선(edge) : 정점 간 관계, 정점을 이어주는 선
✔︎ 인접 정점(adjacent vertex) : 하나의 정점에서 간선에 의해 직접 연결된 정점
✔︎ 가중치 그래프(weighted graph) : 연결의 강도(추가적인 정보)가 얼마나 되는지 적혀있는 그래프
✔︎ 비가중치 그래프(unweighted graph) : 연결의 강도가 적혀있지 않는 그래프
✔︎ 무방향 그래프(undirected graph) : 방향이 정해져 있지 않아 양쪽에서 자유롭게 갈 수 있음
✔︎ 단방향 그래프(directed graph) : 한 방향으로만 갈 수 있음
✔︎ 진입차수(in-degree) / 진출차수(out-degree) : 한 정점에 진입(들어오는 간선)하고 진출(나가는 간선)하는 간선이 몇 개인지 나타낸 것
✔︎ 인접(adjacency) : 두 정점 간 간선이 직접 이어져 있는 것
✔︎ 자기 루프(self loop) : 정점에서 진출한 간선이 바로 자기 자신에게 진입하는 경우, 다른 정점이 거치지 않음
✔︎ 사이클(cycle) : 한 정점에서 출발해 다시 해당 정점으로 돌아오는 것
- Binary Search Tree(BST, 이진 탐색 트리)
⦿ 학습내용
☞ 이진 트리 (Binary Tree)
✔︎ 자식 노드가 최대 두 개인 노드들로 구성된 트리
✔︎ 왼쪽 자식 노드, 오른쪽 자식 노드로 나뉨
☞ 이진 트리의 종류
✔︎ 정 이진 트리(Full Binary Tree) : 각 노드가 0개 혹은 2개의 자식 노드를 가짐
✔︎ 포화 이진 트리(Perfect Binary Tree) : 정 이진 트리면서 완전 이진 트리인 경우. 모든 리프 노드 레벨이 동일하고, 모든 레벨이 가득 차있는 트리
✔︎ 완전 이진 트리(Complete Binary Tree) : 마지막 레벨을 제외한 모든 노드가 가득 차있어야 하고, 마지막 레벨의 노드 왼쪽은 채워져 있어야 함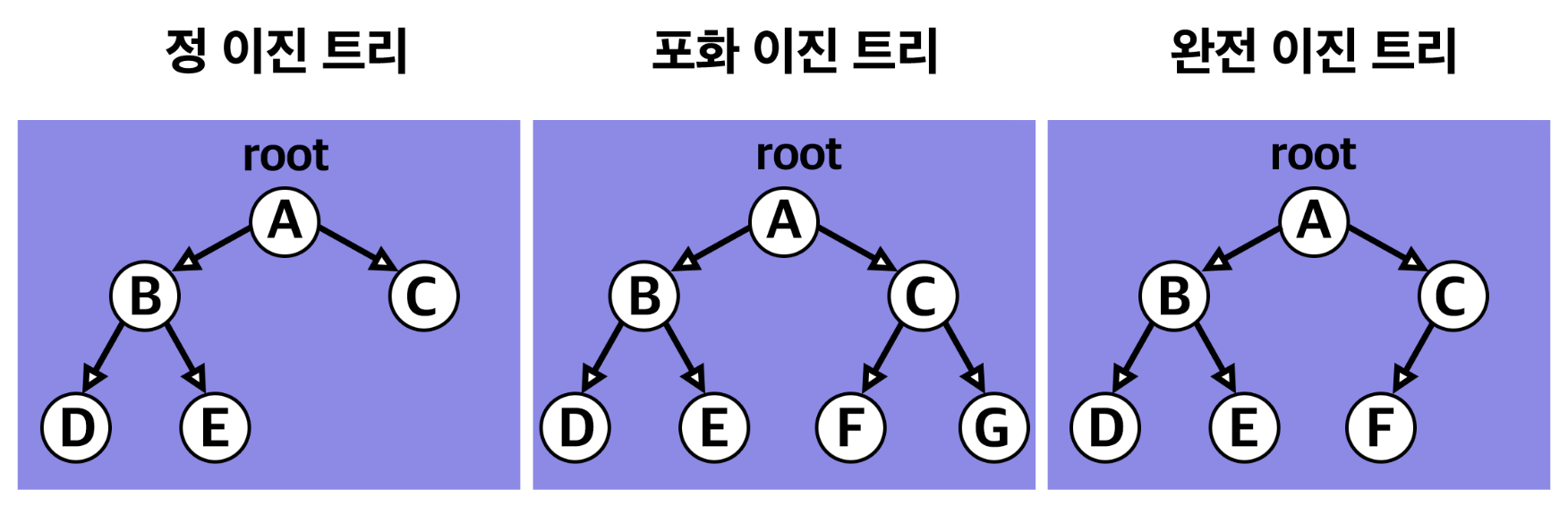
☞ 이진 탐색 트리 (Binary Search Tree)
✔︎ 모든 왼쪽 자식 노드의 값이 부모 노드의 값보다 작고, 모든 오른쪽 자식 노드의 값이 부모 노드의 값보다 큰 값을 가짐
◉ 느낀 점
☞ 자료구조는 이론적으로는 항상 큰 어려움은 없는데, 알고리즘 문제에 적용시키면 정말 까다로운 것 같다 😅 머리가 왜 이렇게 안굴러가지 ,,
한 문제, 한 문제 어떤 자료구조를 어떻게 적용시켜 풀어야할 지 수도코드를 짜는 것부터 연습해야겠다 ,,!! 항상 반복... 또 반복 ... ✍️ ✍️ ✍️
◉ 내일의 키워드
・ Search Algorithm
・ Tree, Graph, BST 문제 풀이 (Coplit) with Pair