Generative model(생성 모델)

• 생성모델: 학습 데이터가 주어졌을 때, 학습 데이터의 분포를 따르는 유사한 데이터를 생성하는 모델
  
• 위의 예시에서 왼쪽 학습 데이터 안에 각 샘플마다 픽셀의 분포를 알 수 있기에, 분포를 제대로 알아낸다면 오른쪽 그림처럼 유사한 데이터를 생성할 수 있음
• 학습 데이터의 분포와의 차이가 적을수록 실제 데이터와 비슷한 데이터를 생성할 수 있음

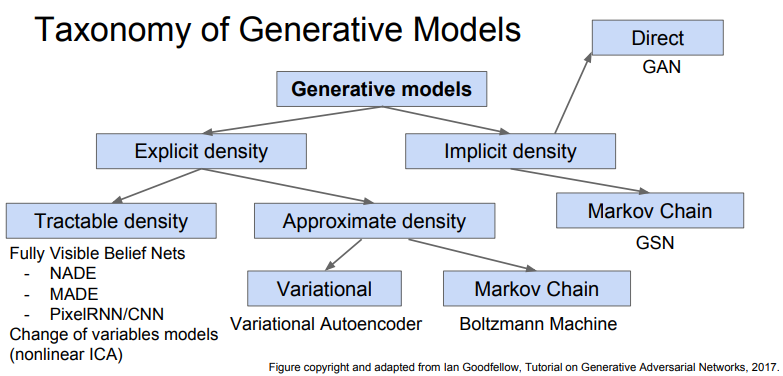
• Explicit density: 학습 데이터의 분포를 기반으로 생성
  • Tractable density: 학습 데이터의 분포를 직접적으로 구하는 방법(PixelRNN/CNN)
  • Approximate density: 분포를 단순히 추정하는 방법(VAE, DDPM)
• Implicit density: 그러한 분포를 몰라도 생성(GAN)

Explicit density

Tractable density

• 학습 데이터의 분포를 학습하기 위해서, 연쇄법칙(Chain rule)을 통해 구할 수 있음
• 이전 픽셀들 값을 통해 현재 픽셀의 값을 결정해서 이미지 전체에 대해 데이터를 생성할 수 있음
• 목표는 위의 함수를 최대화하는 것이며, 복잡한 분포는 Neural Network를 이용해서 표현하면 됨

PixelRNN

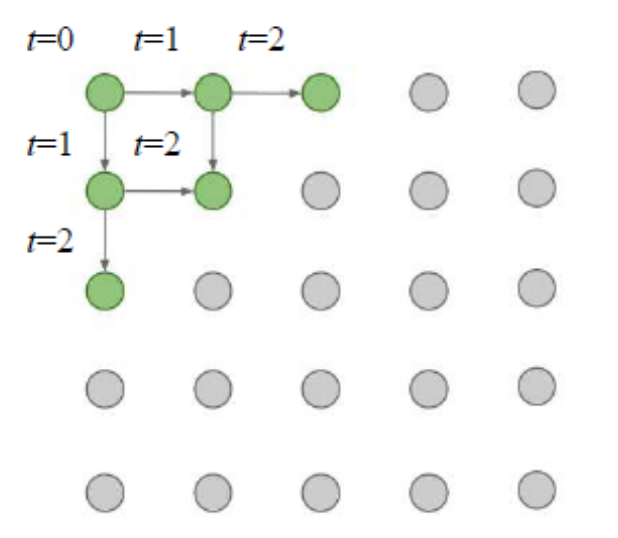
• PixelRNN은 이전 픽셀을 어떻게 정의하는가가 중요함
• 왼쪽 상단 코너의 픽셀부터 오른쪽 하단의 픽셀 방향으로 순서를 잡으면 이전 픽셀에 대한 정의를 할 수 있음
• 이미지의 순서를 정한다면 RNN/LSTM 모델을 사용해 생성할 수 있음
• 하지만 sequential한 생성은 느리다는 단점이 있음

PixelCNN

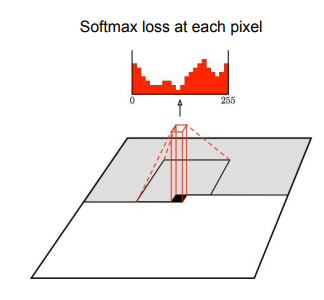
• RixelRNN와 같이 코너에서부터 시작하지만 CNN모델을 사용해 생성함
• PixelRNN보다 학습이 빠르나 여전히 순서 자체를 학습하기 때문에 느림

PixelRNN and PixelCNN

• 장점: 학습 데이터의 이미지 확률 분포 자체를 학습할 수 있고, 확률이 명확하기에 생성된 이미지도 뚜렷함
• 단점: 순서 자체를 학습하기 때문에 속도 측면에서 느림

Approximate density

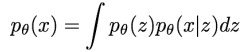
• VAE는 intractable한 latent vector $z$에 대한 density function을 알아내려 함
• 하지만 직접적으로 모델을 학습시킬 수 없고, likelihood의 lower bound를 derive하고 optimize해야 함

Auto Encoder(AE)

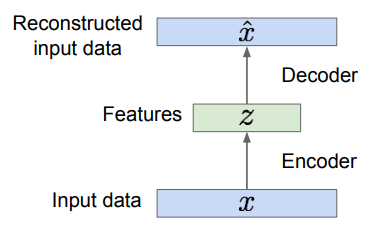
• 라벨링되지 않은 데이터로부터 저차원의 특징을 학습한 비지도학습임
• 오토 인코더는 입력($x$)을 기반으로 특징($z$)을 추출하고, 추출된 특징으로부터 다시 원본 데이터를 출력하는 네트워크임
• 원래의 인코더는 linear+nonlinearity를 통해서 설계되었고, 그 후에 Deep,fc 모델을 통해서, 그 후에는 ReLU, CNN을 통해서 설계됨
• $z$는 $x$로부터 뽑힌 가장 중요한 정보들만 담고 있어야 하기 때문에 $z$는 항상 $x$보다 dimensionality가 축소됨
• AE를 학습시키는 방법은 conv를 이용해서 $x$를 통해 $x$를 복원하며, 손실된 적은 양의 정보($z$) 를 통해서 원본을 복구하기 위해 의미있는 feature만 남음

Variational Auto Encoder(VAE)

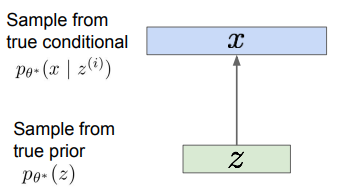
• 훈련 데이터가 관찰 불가능한(latent) $z$로부터 생성되었다고 가정(기존 아이디어를 거꾸로 뒤집음)
• $x$는 이미지, $z$는 벡터이고, 훈련 데이터의 다양한 feature를 나타내고 있다고 가정

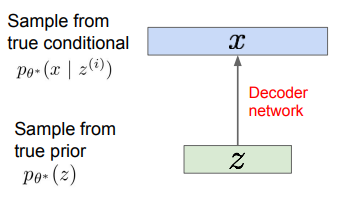
• $z$에 대한 prior $p(z)$는 가우시안이 될 수 있음
• 가우시안으로 된 $p(z)$를 통해 $p(x|z)$를 통해 이미지를 뉴럴 네트워크로 만들어내며, 디코더 네트워크라고 함
• 학습 목표: 훈련 데이터의 likelihood가 maximize되게끔 모델 파라미터를 학습하는 것(훈련 데이터가 복원이 잘 되게끔)

• $p(z)$는 가우시안으로 정했기에 얻어낼 수 있으며, $p(x|z)$는 디코더 네트워크이기 때문에 연산이 가능함. 다만, $\int$를 처리할 수 없음

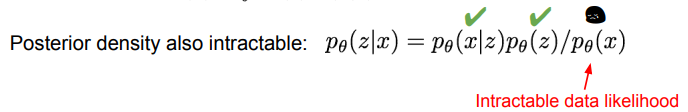
• 베이즈 룰을 적용한 posterior density 또한 구할 수 없음

Solution: Variational inference

• 복잡한 $p(x)$가 있을 때 단순한 $q(x)$로 근사시키는 방법
• 추가적인 인코딩 네트워크 $q(z|x)$를 정의해서 $p(z|x)$를 알아내도록 하는 것

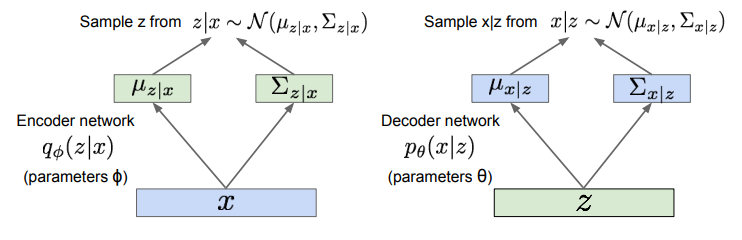
• 인코더 네트워크 $q(z|x)$는 $x$를 입력으로 받아서 $z|x$의 mean과 covariance를 구하고, 디코더 네트워크 $p(x|z)$는 $z$를 입력으로 받아서 $x|z$의 mean과 covariance를 구함
• 이상적인 $z$의 확률 분포를 모르기 때문에, $q$모델로 임의의 가우시안 분포에서 $z$를 샘플링해서 $q(z|x)$를 $p(z|x)$와 근사한 가우시안을 구하게 함. 그리고 $z$를 알게 되었다면 $x$는 $p(x|z)$를 수행하는 디코더 네트워크를 통해 샘플링 할 수 있게 됨

Preliminary

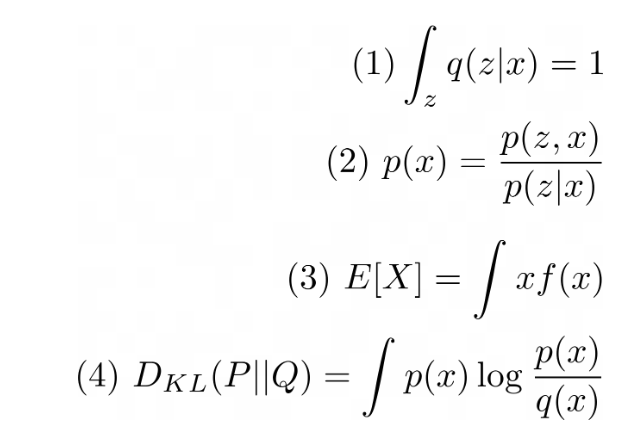
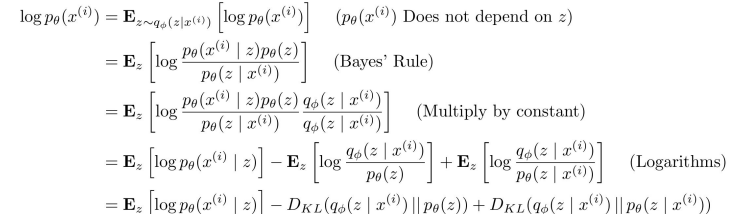
• 우리의 목표를 maximum likelihood estimation을 통해 최적화함

1. log likelihood를 $q_{\phi}(z|x)$로부터 sampling한 latent vector $z$에 대한 expectation식으로 바꿔줄 수 있음(=확률 $p$에 log를 취하고 $q$에 대한 적분 값을 곱해줌. $q$의 적분 값은 1이기에 상관 x)
2. Baye's Rule 적용
3. 분모와 분자에 $q_{\phi}(z|x)$을 곱함
4. log 수식 정리
5. 3개의 term으로 정리

• 첫 번째 term: Decoder Network Term

  • reconstruction: original input being reconstructed
  • $q_{\phi}(z|x)$로부터 sampling한 $z$를 가지고 $p_{\theta}(x_i|z)$가 $x_i$를 생성한 log likelihood

• 두 번째 term: KL term

  • prior $z$와 posterior $q_{\phi}(z|x)$ 사이의 KL-divergence
  • 근사된 posterior의 분포가 얼마나 normal distribution과 가까운지에 대한 척도(prior를 normal distribution으로 가정)

• 세 번째 term: KL term

  • $p_{\theta}(z|x_i)$는 intractable하기 때문에 계산하기 어려움
  • 하지만 KL의 성질에 의해 세 번째 항은 무조건 0보다 크거나 같음

• 첫 번째 term과 두 번째 term을 하나로 묶어주면 원래의 objective function에 대한 tractable한 lower bound(ELBO)를 정할 수 있음

• MLE를 풀기 위해서 objective function을 미분해서 gradient ascent를 해야하는데 lower bound가 정의된다면 lower bound를 최대화하는 문제로 바꿔서 gradient를 구할 수 있음