시간복잡도
알고리즘이 문제를 해결하기 위한 시간(연산)의 횟수
공간복잡도
메모리 사용량
최선/최악/평균의 연산횟수 중 최악의 경우로 알고리즘의 성능을 파악한다.
Big-O 표기법
| O(1) | 상수시간: 입력값 n이 주어졌을 때, 알고리즘이 문제를 해결하는데 오직 한 단계만 거친다. |
| O(log n) | 로그시간: 입력값 n이 주어졌을 때, 문제를 해결하는데 필요한 단계들이 연산마다 특정 요인에 의해 줄어든다. |
| O(n) | 직선적 시간: 문제를 해결하기 위한 단계의 수와 입력값 n이 1:1 관계를 가집니다. |
| O(n^2) | 2차 시간: 문제를 해결하기 위한 단계의 수는 입력값 n의 제곱 |
| O(n^3) | 3차 시간: 문제를 해결하기 위한 단계의 수는 입력값 n의 세제곱 |
| O(C^n) | 문제를 해결하기 위한 단계의 수는 주어진 상수값 C의 n제곱 |
각 자료 구조의 특정 작업(method)별 시간/공간 복잡도 이해하기
배열(Arrays)
배열은 메모리에 연속적으로 저장되기때문에 배열에 저장된 데이터들은 각 데이터들의 옆에 존재한다.
탐색: Lookup(position)
위치를 알고 있기때문에 한 번만 실행하는 것으로 원하는 값을 찾을 수 있다. ⇒ O(1)
지정: Assign
배열에서 값을 변경하고자 하는 경우에도 위치를 알고 있으면 한 번의 실행으로 값을 변경한다. ⇒ O(1)
삽입: Insert
이미 데이터가 저장된 배열 안에서 새로운 값을 특정 주소에 추가하고싶다면, 기존에 존재하는 데이터들을 밀어내서 새로운 공간을 만들어야한다. 밀어내야하는 데이터의 개수만큼 같은 작업을 반복한다. ⇒ O(n)
제거: Remove
삽입과 마찬가지로, 배열의 특정 값을 제거한다면 그 값 뒤에 있었던 데이터들이 모두 앞으로 재배치되어야한다. 재배치되어야하는 데이터의 개수만큼 같은 작업을 반복한다. ⇒ O(n)
검색: Find(value)
인덱스가 아니라 값으로 원하는 값이 어디에 있는 지 찾기 위해서, 배열 처음부터 value가 어디에 있는 지 찾아야한다.
⇒ O(n)
Linked Lists
연결리스트는 배열과 비슷해보이지만 비연속적으로 데이터가 저장되는 구조로, 각 노드는 다음 노드를 가리키는 주소값을 담고 있다. (head/tail)
Lookup(position)
다음 노드를 가리키는 주소값을 따라 연결 리스트를 순회하면서 값을 찾아야한다. ⇒ O(n)
Find(Value)
각 노드들이 가리키는 다음 노드 주소값을 따라 순회하면서 해당하는 값을 가진 노드를 찾아야한다. ⇒ O(n)
Assign
각 노드들이 가리키는 다음 노드 주소값을 따라 순회한 후에 변경해야한다. ⇒ O(n)
Insert
연결 리스트에서는 tail에 다음 노드의 주소값을 추가해서 새 노드와 연결시키는 작업 한 번만 하면 된다. ⇒ O(1)
Removal
head를 삭제할 경우 head 삭제 한 번만 실행 ⇒ O(1)
middle을 삭제할 경우 삭제하려는 노드를 찾을 때까지 계속 노드에 저장된 다음 노드의 주소를 따라 순회해야한다. ⇒ O(n)
Doubly-Linked Lists(이중 연결 리스트)
이중연결 리스트에서는, 각각의 노드는 값과 함께 이전/이후 노드의 주소값을 모두 가지고 있다.
Lookup ⇒ O(n)
Find ⇒ O(n)
Assign ⇒ O(n)
Insert ⇒ O(1)
Remove ⇒ 이미 삭제하려는 노드의 전후 노드를 알고 있기때문에 순회할 필요가 없다. 이전/이후 노드를 연결시켜주면 삭제하려는 노드의 연결이 끊어짐. ⇒ O(1)
Tree

Find
찾으려는 노드의 depth에 따라 시간 복잡도가 선형적으로 증가한다. ⇒ O(n)
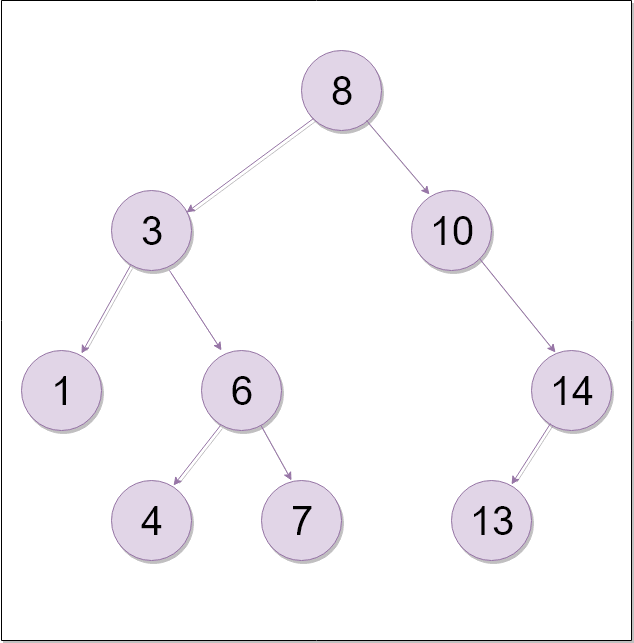
Binary Search Tree
탐색, 삽입, 삭제는 트리의 높이만큼 시간이 걸린다.
Find
ex) 왼쪽 or 오른쪽 노드만 있는 이진 탐색 트리(one long branch)일 경우 Find의 시간 복잡도는 O(n)이 된다.
해결방법? 왼쪽과 오른쪽의 레벨의 차이가 1을 넘지 않게 노드의 부모 자식 관계를 변경한다.
완전 이진트리에서는 루트에서 첫 번째 자식 노드로 가면 탐색해야 하는 노드의 수가 절반으로 줄어듦 (m개 => m/2개)
탐색을 해야하는 노드의 수가 2^n개일 때, 이진 트리는 n번의 탐색으로 값을 찾을 수 있다. n = log_2(2^n) ⇒ O(log n)
Insert
ex) one long branch일 경우, leaf까지 도달한 후에 노드를 추가해야한다. ⇒ O(n)
Delete
마찬가지로 삭제하려는 노드가 있는 층까지 도달해야하기때문에 순회하는 높이만큼 선형적으로 시간 복잡도가 증가한다. ⇒ O(n)
