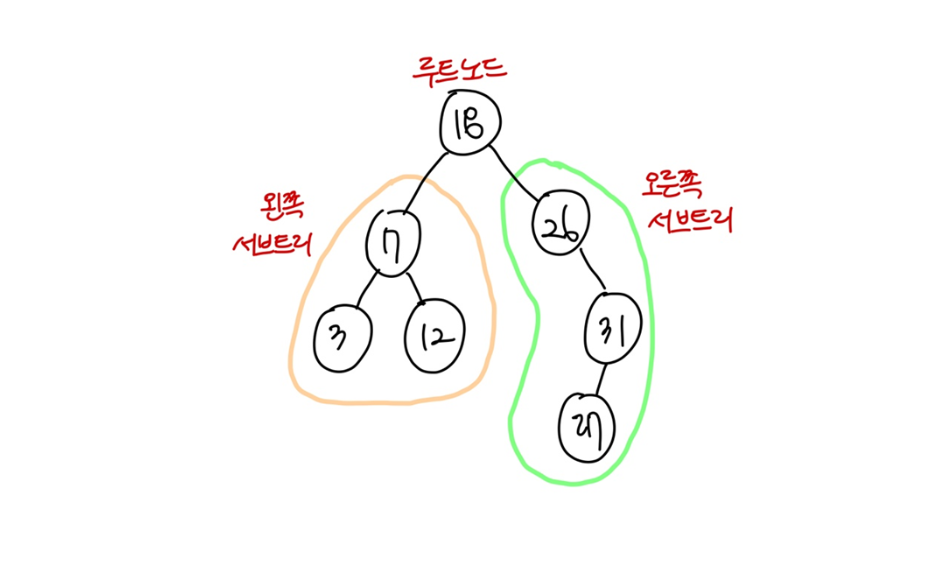
이진 탐색 트리(BST, Binary Search Tree)
key(왼쪽서브트리) < key(루트노드) < key(오른쪽서브트리)
- 모든 노드는 중복될 수 없다
- inorder traversal(중위 순회)하면 오름차순으로 정렬된 값을 얻을 수 있다
이진 탐색 트리 연산
탐색 연산(search)
search(key)
키 값이 key인 노드를 찾아 반환한다
-
비교한 결과가 같으면?
탐색이 끝난다 -
키 값이 루트보다 작으면?
왼쪽 서브트리 탐색한다 -
키 값이 루트보다 크면?
오른쪽 서브트리 탐색한다
삽입 연산(insert)
insert(n)
새 노드 n을 삽입하고도 이진 탐색 트리의 특징을 잘 유지해야 한다
- 먼저 탐색 수행을 시작한다
(=키 값이 루트보다 작으면 왼쪽 서브트리로, 키 값이 루트보다 크면 오른쪽 서브트리로 이동해서 탐색) - 탐색에 실패하면?
그 위치가 새 노드를 삽입할 위치가 된다
주의) 만약 삽입하려는 수가 이미 트리에 존재하는 수인 경우에는 트리에 삽입할 수 없다
삭제 연산(delete)
delete(n)
노드 n을 삭제하고도 이진 탐색 트리의 특징을 잘 유지해야 한다
삭제하려는 노드가 단말 노드일 경우
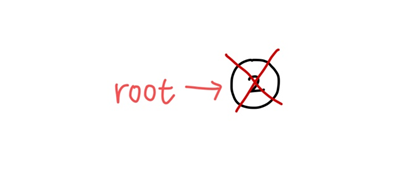
1. 제거 노드가 루트 노드인 경우
-> 루트를 NULL로 바꾼다
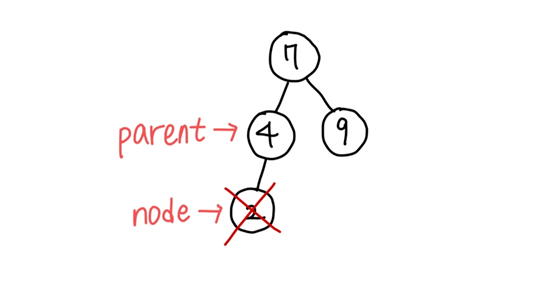
2. 제거 노드가 부모 노드의 왼쪽 자식인 경우
-> 부모 노드의 왼쪽 링크를 NULL로 바꾼다
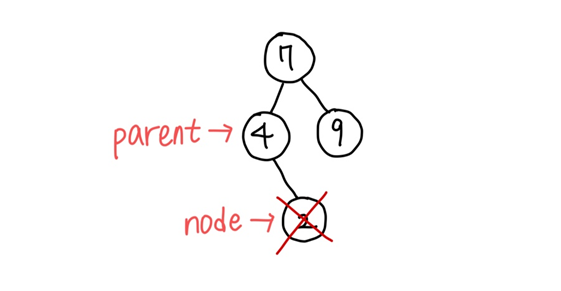
3. 제거 노드가 부모 노드의 오른쪽 자식인 경우
-> 부모 노드의 오른쪽 링크를 NULL로 바꾼다
삭제하려는 노드가 왼쪽이나 오른쪽 서브 트리 중 하나만 가지고 있는 경우
-
제거 노드가 루트 노드인 경우
-> 제거 노드의 child가 루트 노드가 된다
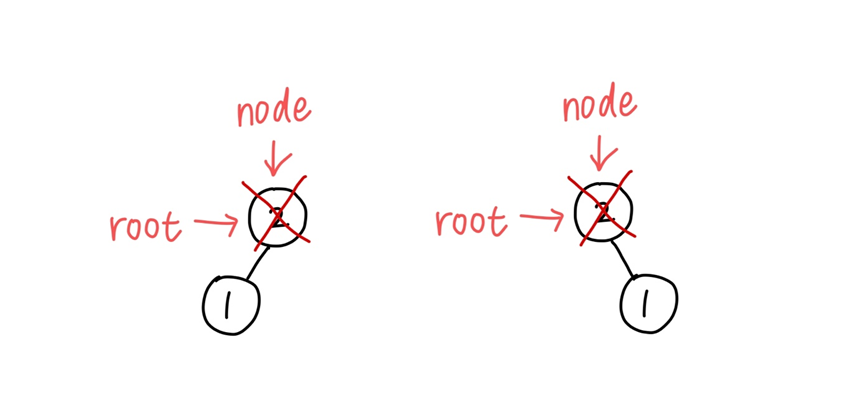
-
제거 노드가 부모 노드의 왼쪽 자식인 경우
-> 부모 노드의 왼쪽에 제거 노드의 child를 연결한다
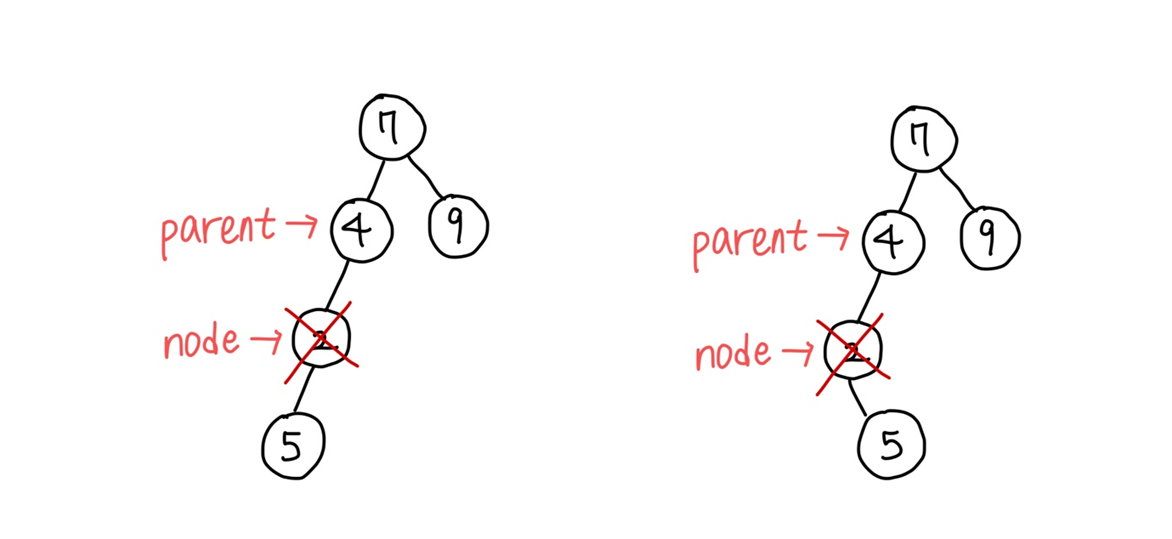
-
제거 노드가 부모 노드의 오른쪽 자식인 경우
-> 부모 노드의 오른쪽에 제거 노드의 child를 연결한다
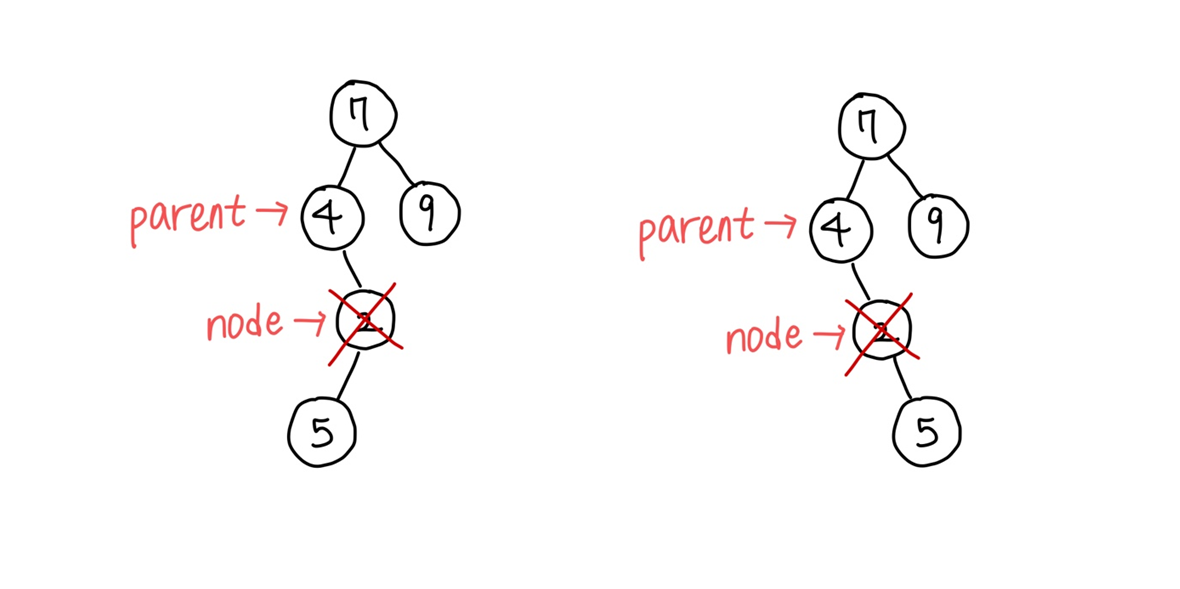
삭제하려는 노드가 두 개의 서브트리를 모두 가지고 있는 경우
삭제하려는 노드를 삭제한다 -> leftmost node와 rightmost node 둘 중 삭제한 노드와 차이가 더 적은 노드를 삭제 노드의 위치로 가져온다
- leftmost node : 오른쪽 서브 트리에서 제일 작은 값
- rightmost node : 왼쪽 서브 트리에서 제일 큰 값
이진 탐색 트리 클래스(BinSrchTree)
아래는 기존에 사용하던 BinaryNode 클래스와 BinaryTree 클래스 코드이다
기존의 BinaryNode 클래스
// BinaryNode 클래스
class BinaryNode {
public:
int data;
BinaryNode* left;
BinaryNode* right;
BinaryNode(int val = 0, BinaryNode* l = NULL, BinaryNode* r = NULL)
:data(val), left(l),right(r){}
~BinaryNode(){}
int setData(int val) {
data = val;
}
void setLeft(BinaryNode* l) {
left = l;
}
void setRight(BinaryNode* r) {
right = r;
}
int getData() {
return data;
}
BinaryNode* getLeft() {
return left;
}
BinaryNode* getRight() {
return right;
}
bool isLeaf() {
return left == NULL && right == NULL;
}
};기존의 BinaryTree 클래스
// BinaryTree 클래스
class BinaryTree {
BinaryNode* root;
public:
BinaryTree()
:root(NULL){}
~BinaryTree(){}
void setRoot(BinaryNode* node) {
root = node;
}
BinaryNode* getRoot() {
return root;
}
bool isEmpty() {
return root == NULL;
}
int getCount() {
return isEmpty() ? 0 : getCount(root);
}
int getCount(BinaryNode* node) {
if (node == NULL) {
return 0;
}
else {
return 1 + getCount(node->getLeft()) + getCount(node->getRight());
}
}
int getHeight() {
return isEmpty() ? 0 : getHeight(root);
}
int getHeight(BinaryNode* node) {
if (node == NULL) {
return 0;
}
int hLeft = getHeight(node->getLeft());
int hRight = getHeight(node->getRight());
return (hLeft > hRight) ? 1 + hLeft : 1 + hRight;
}
int getLeafCount() {
return isEmpty() ? 0 : getLeafCount(root);
}
int getLeafCount(BinaryNode* node) {
if (node == NULL) {
return 0;
}
if (node->isLeaf()) {
return 1;
}
else {
return getLeafCount(node->getLeft()) + getLeafCount(node->getRight());
}
}
bool isFull() {
return isEmpty() ? 0 : isFull(root);
}
bool isFull(BinaryNode* node) {
if (node == NULL) {
return 0;
}
if (node->left == NULL && node->right == NULL) {
return true;
}
if (node->left != NULL && node->right != NULL) {
return isFull(node->left) and isFull(node->right);
}
else return false;
}
int calcLevel(int n) {
return isEmpty() ? 0 : calcLevel(root, n, 1);
}
int calcLevel(BinaryNode* node, int n, int level) {
if (node == NULL) {
return 0;
}
if (node->data == n) {
return level;
}
int ll = calcLevel(node->left, n, level + 1);
if (ll != 0) {
return ll;
}
ll = calcLevel(node->right, n, level + 1);
return ll;
}
};하지만 이 코드에서 한 가지 수정해야 하는 부분이 있다 BinSrchTree 클래스에서 멤버 변수 root 노드에 접근할 수 있도록 해야하기 때문에 private에서 protected로 변경해야 한다
수정된 BinaryTree 클래스
// 기존 코드
private:
BinaryNode* root;
// 수정된 코드
protected:
BinaryNode* root;한 줄만 수정되었다
// 수정된 BinaryTree 클래스
class BinaryTree {
protected: // 수정된 부분
BinaryNode* root;
public:
BinaryTree()
:root(NULL){}
~BinaryTree(){}
void setRoot(BinaryNode* node) {
root = node;
}
BinaryNode* getRoot() {
return root;
}
bool isEmpty() {
return root == NULL;
}
int getCount() {
return isEmpty() ? 0 : getCount(root);
}
int getCount(BinaryNode* node) {
if (node == NULL) {
return 0;
}
else {
return 1 + getCount(node->getLeft()) + getCount(node->getRight());
}
}
int getHeight() {
return isEmpty() ? 0 : getHeight(root);
}
int getHeight(BinaryNode* node) {
if (node == NULL) {
return 0;
}
int hLeft = getHeight(node->getLeft());
int hRight = getHeight(node->getRight());
return (hLeft > hRight) ? 1 + hLeft : 1 + hRight;
}
int getLeafCount() {
return isEmpty() ? 0 : getLeafCount(root);
}
int getLeafCount(BinaryNode* node) {
if (node == NULL) {
return 0;
}
if (node->isLeaf()) {
return 1;
}
else {
return getLeafCount(node->getLeft()) + getLeafCount(node->getRight());
}
}
bool isFull() {
return isEmpty() ? 0 : isFull(root);
}
bool isFull(BinaryNode* node) {
if (node == NULL) {
return 0;
}
if (node->left == NULL && node->right == NULL) {
return true;
}
if (node->left != NULL && node->right != NULL) {
return isFull(node->left) and isFull(node->right);
}
else return false;
}
int calcLevel(int n) {
return isEmpty() ? 0 : calcLevel(root, n, 1);
}
int calcLevel(BinaryNode* node, int n, int level) {
if (node == NULL) {
return 0;
}
if (node->data == n) {
return level;
}
int ll = calcLevel(node->left, n, level + 1);
if (ll != 0) {
return ll;
}
ll = calcLevel(node->right, n, level + 1);
return ll;
}
};⭐BinSrchTree 클래스
// BinSrchTree 클래스
class BinSrchTree :public BinaryTree { // BinaryTree로부터 상속받는다
public:
BinaryNode* search(int key) {
BinaryNode* node = search(root, key);
return node;
}
BinaryNode* search(BinaryNode* n, int key) {
if (n == NULL) return NULL;
if (n->getData() == key) return n;
else if (n->getData() > key) {
search(n->getLeft(), key);
}
else {
search(n->getRight(), key);
}
}
void insert(BinaryNode* n) {
if (n == NULL) return;
if (isEmpty()) root = n; // 빈 트리라는 의미이므로 삽입하려는 노드가 루트 노드가 된다
else insert(root, n);
}
void insert(BinaryNode* r, BinaryNode* n) {
if (n->getData() == r->getData()) return; // 이미 존재하는 노드라면 삽입할 수 없다
else if (n->getData() < r->getData()) {
if (r->getLeft() == NULL) r->setLeft(n);
else insert(r->getLeft(), n);
}
else {
if (r->getRight() == NULL) r->setRight(n);
else insert(r->getRight(), n);
}
}
void remove(BinaryNode* parent, BinaryNode* node) {
// case1: 삭제하려는 노드가 단말 노드인 경우
if (node->isLeaf()) {
if (parent == NULL) root = NULL;
else if (parent->getLeft() == node) parent->setLeft(NULL);
else parent->setRight(NULL);
}
// case2: 삭제하려는 노드가 서브트리 중 하나만 가지고 있는 경우
else if (node->getLeft() == NULL || node->getRight() == NULL) {
BinaryNode* child = (node->getLeft() != NULL) ? node->getLeft() : node->getRight();
if (node == root) root = child;
else if (parent->getLeft() == node) parent->setLeft(child);
else parent->setRight(child);
}
// case3: 삭제하려는 노드가 두 개의 서브트리 모두 가지고 있는 경우
else {
// leftmost
BinaryNode* succp = node;
BinaryNode* succ = node->getRight();
while (succ->getLeft() != NULL) {
succp = succ;
succ = succ->getLeft();
}
// rightmost
BinaryNode* succp2 = node;
BinaryNode* succ2 = node->getLeft();
while (succ2->getRight() != NULL) {
succp2 = succ2;
succ2 = succ2->getRight();
}
//비교
int dL = abs(node->getData() - succ->getData());
int dR = abs(node->getData() - succ2->getData());
//차이 더 적은 것
if (dL < dR) {
// leftmost 선택
if (succp->getLeft() == succ) succp->setLeft(succ->getRight());
else succp->setRight(succ->getRight());
node->setData(succ->getData());
node = succ;
}
else {
// rightmost 선택
if (succp2->getLeft() == succ2) succp2->setLeft(succ2->getLeft());
else succp2->setRight(succ2->getLeft());
node->setData(succ2->getData());
node = succ2;
}
delete node;
}
}
};