Image Transformation

• spatial domain 신호는 frequency domain 신호로 변환된다
• frequency domain 신호도 spatial domain 신호로 변환될 수 있다
• 신호가 변환되는 과정에서 정보 손실은 없다
  
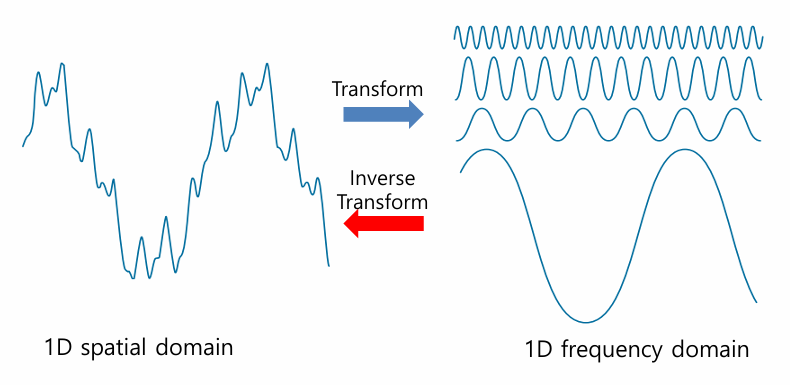
  <푸리에의 아이디어>
  주기 함수는 사인과 코사인의 가중치 합으로 표현할 수 있다
  -> 그렇다면 주기를 무한대로 설정하면 주기 함수는 어떤 함수라도 될 수 있다!

f(x)가 1차원 공간 영역의 신호라고 가정하고, 4개의 주기 함수는 cos(8θ), cos(4θ), cos(2θ), cos(θ)라고 가정하자

 f(x) = 0.2xcos(8θ) + 0.4xcos(4θ) + 0.3xcos(2θ) + 1xcos(θ)

변환의 결과는 주파수 성분이 얼마나 강한지를 나타내는 0.2, 0.4, 0.3, 1과 같은 계수를 찾아내는 것!

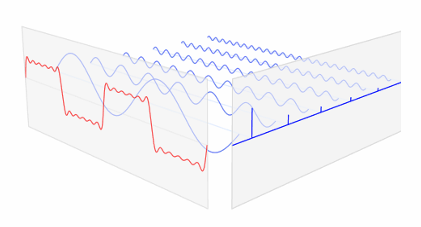빨간색 신호는 기저 함수로 정의된 파란색 신호(사인 및 코사인)의 가중 합이다

Basis Functions of Image

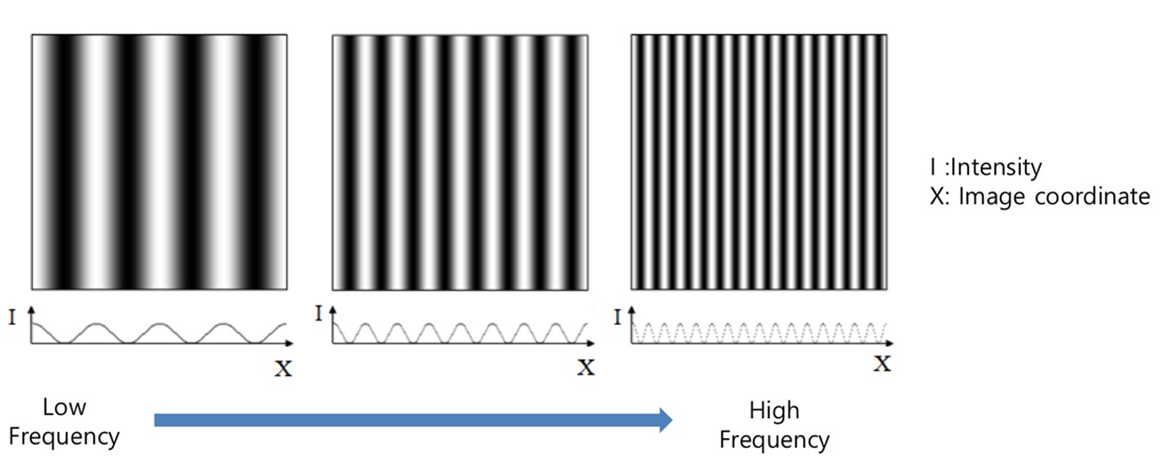
• Intensity는 pixel value이다
• RGB format을 사용한다면 R, G, B가 intensity
• YCbCr format을 사용한다면 Y, Cr, Cb가 intensity

Period

현재 peak와 다음 peak의 시간을 period라고 한다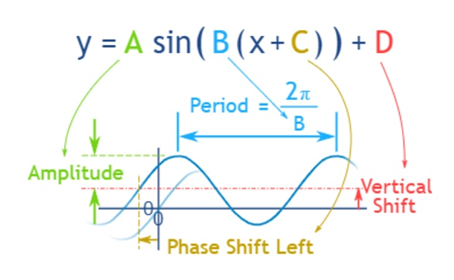

Discrete vs Continuous

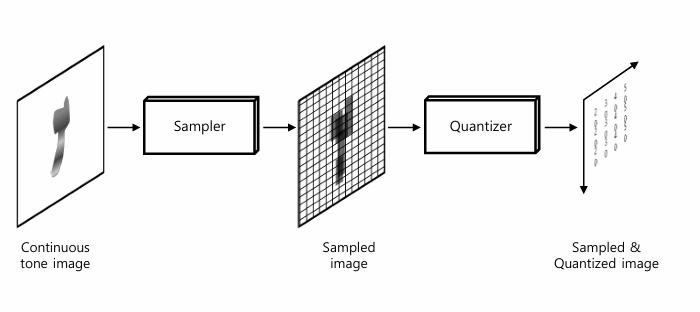
• Discrete = 이산
• sampling을 통해서 디지털 이미지를 얻는다

Discrete Fourier Transform

컴퓨터에서 다루는 신호는 이산 신호다 따라서 컴퓨터에서의 푸리에 변환은 모두 이산 푸리에 변화에 기반을 둔다

Discrete Fourier Transform(이산 푸리에 변환)은 이산 시간에 대한 신호와 이산 주파수 신호 간의 변환이다

Block based Discrete Cosine Transform (DCT)

• 계산 복잡성, 메모리 사용, 졍렬 처리에 강하다
• 이미지 및 비디오 압축에 잘 사용된다