Algorithm with Math
"어떤 방법을 사용해서 풀어 볼래?"라는 질문은 수학적 사고, 즉 "컴퓨팅 사고를 할 수 있어?"라고 물어보는 것
수학적 사고를 이용한 문제 해결 전략(컴퓨팅 사고)
GCD / LCM
약수: 어떤 수를 나누어떨어지게 하는 수
배수: 어떤 수의 1, 2, 3…. 배하여 얻는 수
공약수: 둘 이상의 수들의 공통인 약수
공배수: 둘 이상의 수들의 공통인 배수
최대 공약수(GCD. Greatest Common Divisor): 둘 이상의 공약수 중에서 최대인 수
최소 공배수(LCM. Least Common Multiple): 둘 이상의 공배수 중에서 최소인 수
순열 / 조합
문제: 카드 뽑기
[A, B, C, D, E] 5장의 카드를 갖고 있습니다. 이 5장의 카드 중 3장을 선택하여 나열
- 순서를 생각하며 3장을 선택
- 순서를 생각하지 않고 선택
순열 : n 개의 무언가 중 일부만을 선택하여 나열하는 것(순서를 생각하며 나열)
1번 조건- 1장씩 나열하면서 필요한 장수까지 도달하면 중지
1장째의 카드를 선택하는 방법에는 5가지
그 각각에 대해 2번째 카드를 선택하는 방법에는 4가지
그 각각에 대해 3번째 카드를 선택하는 방법에는 3가지
5 X 4 X 3 = 60
Permutation의 약자 P로 표현
5장에서 3장을 선택하는 모든 순열의 수 = 5P3 = (5 X 4 X 3 X 2 X 1) / (2 X 1) = 60
일반식 :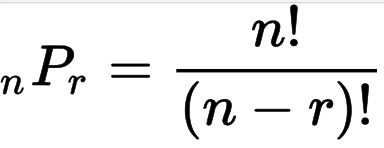 
! 팩토리얼(factorial): n! 은 n 보다 작거나 같은 모든 양의 정수의 곱
조합
2번 조건에서 모든 가짓수를 구할 때는 3장을 하나의 그룹으로 선택
- 순열과 마찬가지로 순서를 생각하며 셈(3장씩 중 중복된 종류도 일단 세봄)
- 중복해서 센 부분으로 나눗셈
순서를 생각하는 바람에 중복된 부분이 발생함으로 순열의 모든 가짓수를 중복되는 6가지로 나누면 조합의 모든 가짓수를 얻을 수 있다.
(5 X 4 X 3 X 2 X 1) / ((3 X 2 X 1) X (2 X 1)) = 10
Combination의 약자 C로 표현
5장에서 3장을 선택하는 모든 조합의 수 = 5C3 = 5! / (3! * 2!) = 10
일반식: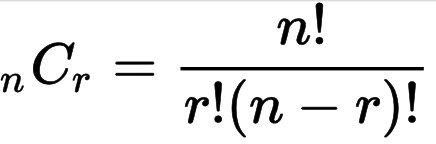 
n개 중 r개를 선택하는 경우의 수(순서x)
ex) 햄버거 가게에 기서 햄버거 5종류 중 2가지, 음료 3종류 중 1가지를 시키는 경우의 수
5C2 * 3C1 -> 5!/3!2! * 3!/2! ---> 10 * 3 = 30
멱집합
나열 방법에서 단계를 나누는 기준은 가장 앞 원소(혹은 임의의 집합 원소)가 있는지, 없는지
집합 {1, 2, 3}이 있다고 했을 때 집합 {1, 2, 3}의 모든 부분집합을 구하면 {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} 이렇게 나열할 수 있고 개수는 8개
트리와 비슷한 모양 - 순환 구조, 임의의 원소를 제외하면서 집합을 작은 단위로 줄여나가는 방법. 즉, 문제를 작은 단위로 줄여나가는 재귀의 응용으로 활용됨
