Tree

Tree?

• 트리는 그래프의 한 종류로, '최소 연결 트리'라고도 불린다.
• 비선형구조는 선형구조(데이터들을 순차적으로 나열시킨 형태)와 다르게 데이터가 계층적으로 구성되어 있다.
• linked list의 단점인 검색 시 노드의 처음부터 찾아가야하는 점을 보완하였다. 검색을 중간부터 시작하여 좌우 중 하나로 분기, 1/2씩 검색 대상을 줄여나감으로써 이진검색의 효과를 얻는다.

[linked list]

[tree]

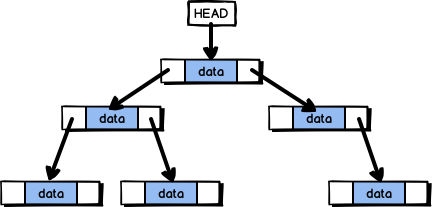
• 트리는 하나의 루트 노드를 갖는다.
• 트리는 DAG(Directed Acyclic Graphs, 방향성이 있는 비순환 그래프)의 한 종류로 사이클이 없다.
• 노드가 N개인 트리는 항상 N-1의 edge를 가진다.
• 트리는 이진 트리(Binary Tree), 이진 탐색 트리(Binary Search Tree, BST), 균형 트리(AVL 트리, red-black 트리), 이진 힙(최대힙, 최소힙) 등이 있다.

Tree 관련 용어

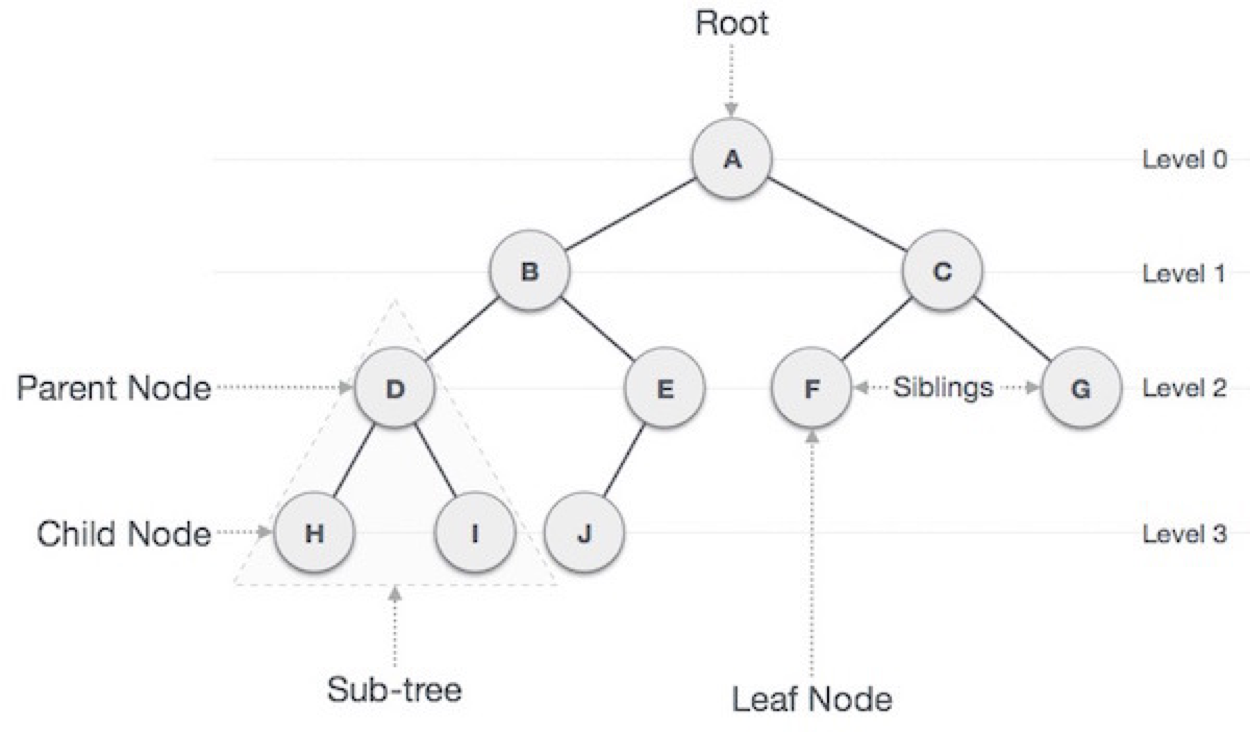
• Node : 트리의 구성요소에 해당하는 A,B,C,D,E,F,G,H,I,J와 같은 요소
• root node : 부모가 없는 노드, 트리에서 최상위에 존재하는 A와 같은 노드. 트리는 하나의 루트 노드만을 가진다.
• leaf node(terminal node) : 자식이 없는 노드, 밑으로 또 다른 노드가 연결되어 있지 않은 H,I,J,F,G와 같은 노드. ‘말단 노드’ 또는 ‘잎 노드’라고도 부른다.
• internal node(내부 노드) : 단말 노드가 아닌 노드
• edge(간선) : 노드를 연결하는 선 (link, branch 라고도 부름)
• sibling(형제): 같은 부모를 가지는 노드
• size(노드의 크기): 자신을 포함한 모든 자손 노드의 개수
• sub-tree : 큰 트리(전체)에 속하는 작은 트리
• level : 트리에서 각 층별로 숫자를 매김
• height : 트리의 최고 레벨 (그림상 3)
• depth(깊이) : root에서 어떤 노드에 도달하기 위해 거쳐야하는 edge의 수
• degree(차수) : 하위 트리 개수/간선 수

Tree 종류

이진 트리(Binary Tree)

각 노드가 최대 두개의 자식을 갖는 트리

정 이진 트리(Full Binary Tree)

• 모든 레벨이 꽉 찬 이진 트리
• 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리
  

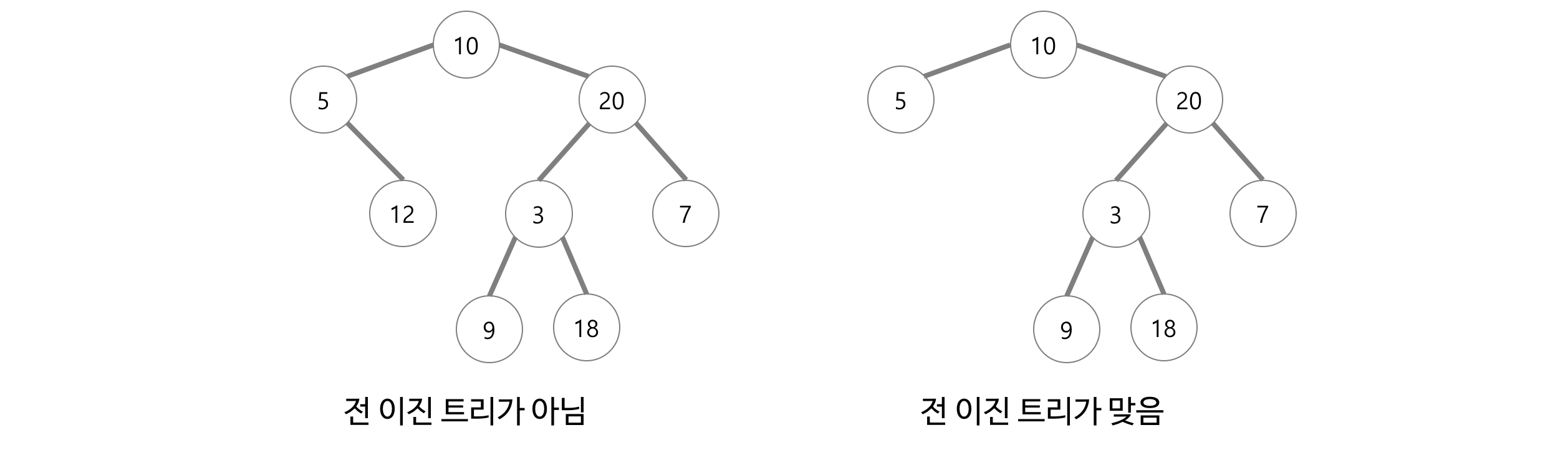
완전 이진 트리(Complete Binary Tree)

• 포화 이진 트리처럼 모든 레벨이 꽉 찬 상태는 아니지만, 자식 노드가 왼쪽에서부터 차례로 채워져있는 이진 트리.
• 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있다.
• 노드가 왼쪽에서 오른쪽으로 채워져야 한다.
  

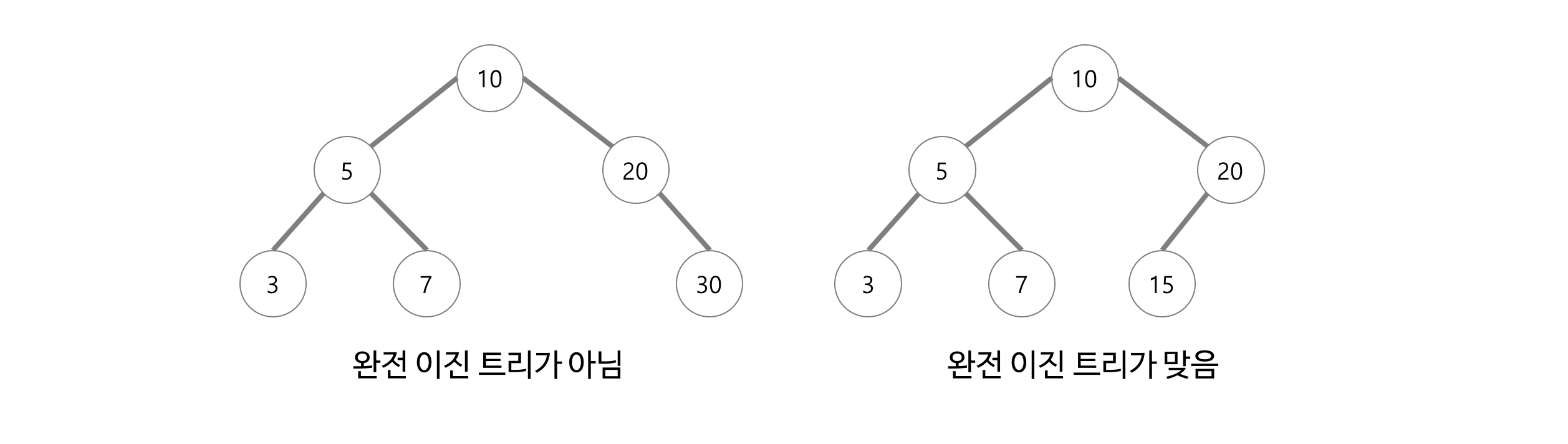
포화 이진 트리(Perfect Binary Tree)

• 모든 내부 노드가 두개의 자식 노드를 가진다.
• 모든 말단 노드는 같은 높이에 있어야 한다.
  

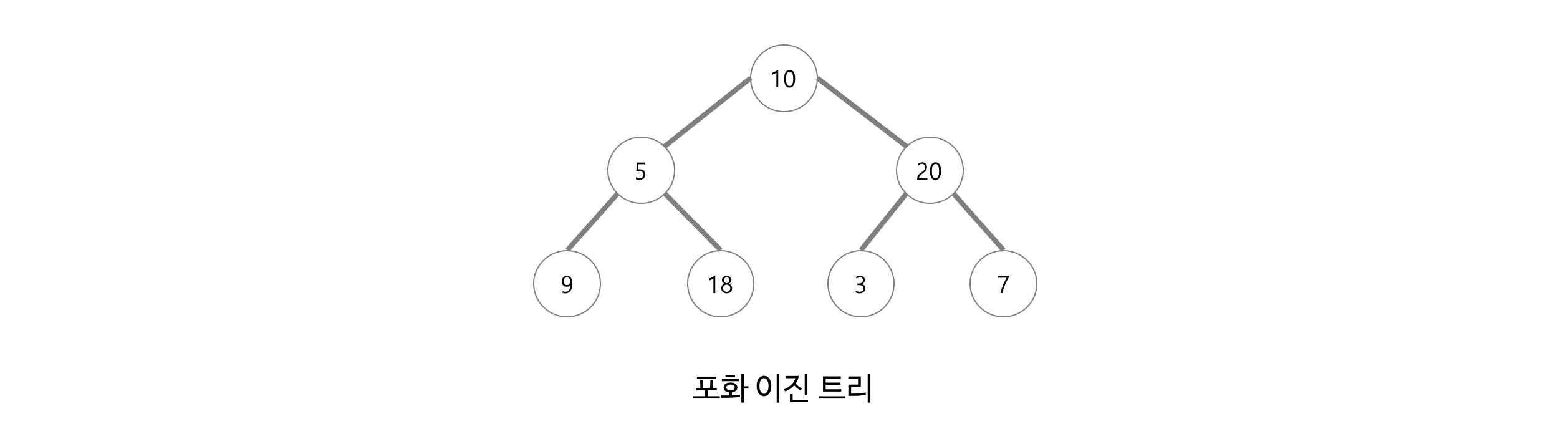
삼항 트리(Ternary Tree)

• 각 노드가 최대 3개의 자식을 갖는 트리

이진 검색 트리(Binary Search Tree)

• 기준이 되는 노드의 왼쪽 자식 노드는 기준 노드보다 크기가 작아야하고, 기준 노드의 오른쪽 자식 노드는 기준 노드보다 커야한다.
• 각 노드의 값은 중복되지 않는다.
• 위와 같은 이유로 일반 이진 트리보다 값을 찾기가 쉽다.
• 주요 연산 : 검색(retreive), 삽입(insert), 삭제(delete)

구현 - 이진 트리

class Tree(object):
    def __init__(self):
        self.left = None
        self.right = None
        self.data = None 

root = Tree()
root.data = "root"
root.left = Tree()
root.left.data = "left"
root.right = Tree()
root.right.data = "right"

참고 사이트
https://gmlwjd9405.github.io/2018/08/12/data-structure-tree.html
https://monsieursongsong.tistory.com/6