시계열 - Stationary 시계열

Nam Eun-Ji·2021년 2월 26일
2

Stationary 시계열

사실상 미래 예측은 불가능하다. 그럼에도 불구하고 미래를 예측하고자 한다면,

  • 과거의 데이터에 일정한 패턴이 존재하며,
  • 과거의 패턴은 미래에도 동일하게 반복될 것이다.

라는 2가지 전제하에 예측이 가능하다. 이 2가지 전제를 한마디로 말하자면 안정적(stationary) 데이터에 대해서만 미래예측이 가능하다는 것이다. 여기서 안정적이란, 시계열 데이터의 통계적 특성이 변하지 않는다는 뜻이다.


안정적 시계열 특징

  1. 시간의 추이와 관계 없이 평균이 불변
  2. 시간의 추이와 관계 없이 분산이 불변
  3. 두 시점 간의 공분산이 기준시점과 무관

공분산
공분산, 상관계수 개념 참고하기
X(t)와 X(t+h) 사이의 공분산과 X(t-h)와 X(t) 사이의 공분산은 X가 stationary한 시계열 변수라는 조건 하에서 일정하다. 즉, 안정적 시계열에 한해서 시차 h가 같다면 데이터의 상관성이 동일한 주기성이 나타난다.

예를들어 2022년의 판매량을 5년치의 데이터를 가지고 예측하고자 할 때,
t에 무관하게 X(t-4), X(t-3), X(t-2), X(t-1), X(t)의 평균과 분산이 일정 범위 안에 있어야하고, X(t-h)와 X(t)는 t에 무관하게 h에 대해서만 달라지는 일정한 상관도를 가져야 한다.


시계열 생성 및 분석

시계열 데이터는 인덱스가 날짜 혹은 시간인 데이터를 말한다.
아래 예제는 Daily Minimum Temperatures in Melbourne 데이터로 온도변화를 나타내는 데이터이다. 이 데이터를 시계열 데이터로 변환하고자 한다.

1. 시계열데이터로 변환

import os
import numpy as np
import pandas as pd

dataset_filepath = os.getenv('HOME') + '/aiffel/stock_prediction/data/daily-min-temperatures.csv'

# Date를 index_col로 지정, index_col: 해당 열을 index로 지정해준다.
df = pd.read_csv(dataset_filepath, index_col='Date', parse_dates=True)
print(type(df))  # <class 'pandas.core.frame.DataFrame'>

# 위 코드까지 했을 때 시간 컬럼이 index가 되었지만, 아직도 type은 dataframe으로 나온다.
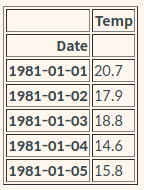
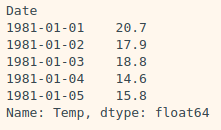
ts1 = df['Temp']
print(type(ts1))  # <class 'pandas.core.series.Serie'>
dfts1

2. 결측치 확인

참고 - Pandas에서 결측치 보간을 처리하는 메소드

from matplotlib.pylab import rcParams

rcParams['figure.figsize'] = 13, 6  # matlab 차트의 기본 크기를 13, 6으로 지정
plt.plot(ts1)  # 시계열(time series) 데이터를 차트로 그려보기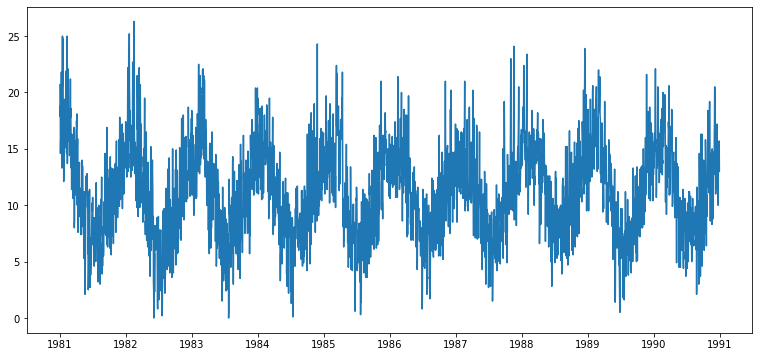

# 결측치 확인
print(ts1[ts1.isna()])

# 결측치가 있다면 보간해주기
ts1=ts1.interpolate(method='time')

# 보간 이후 결측치(NaN) 유무를 다시 확인
print(ts1[ts1.isna()])

3. 통계적 특성 분석

  • 일정 시간 내 구간 통계치(Rolling Statistics) 시각화
  • pandas.Series.rolling : 동일한 사이즈만큼 옆으로 이동하면서 연산
  • pandas.Series.rolling().mean() : 이동평균
  • pandas.Series.rolling().std() : 이동표준편차
# 일정 시간 내 구간 통계치(Rolling Statistics) 시각화하는 함수
def plot_rolling_statistics(timeseries, window=12):
    rolmean = timeseries.rolling(window=window).mean()  # 이동평균 시계열
    rolstd = timeseries.rolling(window=window).std()    # 이동표준편차 시계열

     # 원본시계열, 이동평균, 이동표준편차를 plot으로 시각화해 본다.
    orig = plt.plot(timeseries, color='blue',label='Original')    
    mean = plt.plot(rolmean, color='orange', label='Rolling Mean')
    std = plt.plot(rolstd, color='black', label = 'Rolling Std')
    plt.legend(loc='best')
    plt.title('Rolling Mean & Standard Deviation')
    plt.show(block=False)
    
    
plot_rolling_statistics(ts1, window=12)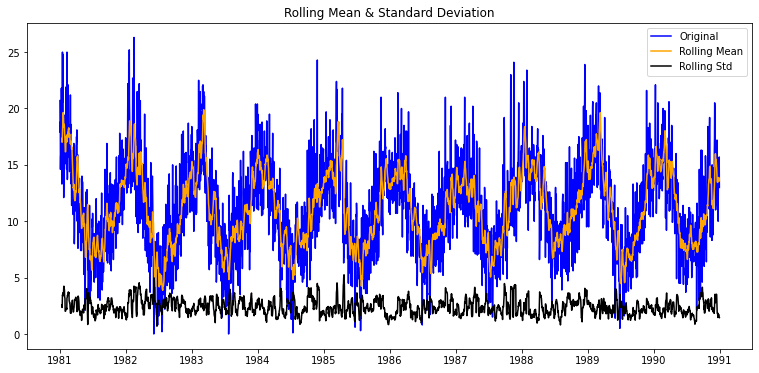


4. 불안정적 시계열 데이터 분석

아래는 International airline passengers 데이터셋으로 월별 항공 승객 수(천명 단위)의 시계열 데이터로 위의 기온변화 데이터와는 다른 패턴이 보인다. 시간의 추이에 따라 시계열의 평균과 분산이 지속적으로 커지는 패턴을 보이는데, 이러한 패턴을 보인다면 이 시계열 데이터는 적어도 안정적이진 않다고 정성적인 결론을 내려볼 수 있을 것 같다. 

dataset_filepath = os.getenv('HOME')+'/aiffel/stock_prediction/data/airline-passengers.csv' 
df = pd.read_csv(dataset_filepath, index_col='Month', parse_dates=True).fillna(0)  
ts2 = df['Passengers']
plot_rolling_statistics(ts2, window=12)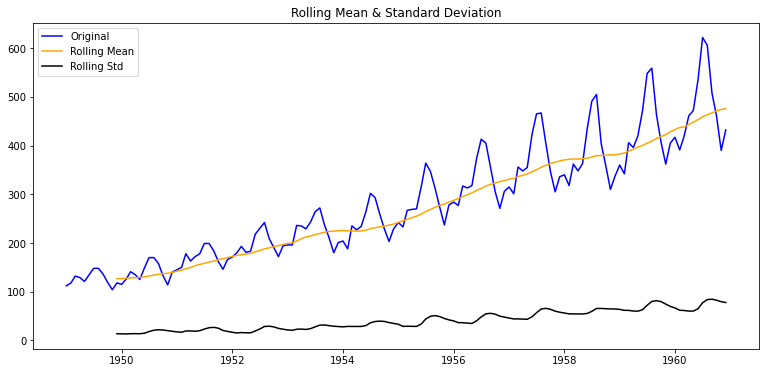

Augmented Dickey-Fuller Test(ADF Test)

  • 시계열 데이터의 안정성을 테스트하는 통계적 방법
  • 주어진 시계열데이터가 안정적이지 않다는 귀무가설을 세운 후 통계적 가설 검정 과정을 통해 이 귀무가설이 기각될 경우, 이 시계열 데이터가 안정적이다라는 대립가설을 채택한다.
  • statsmodels 패키지의 adfuller메소드 : ADF Test 결과
  • P-value : 유의확률
    • 귀무가설이 맞다는 전제 하에, 표본에서 실제로 관측된 통계치와 '같거나 더 극단적인' 통계치가 관측될 확률
    • 귀무가설의 가정이 틀렸다고 볼 수도 있는 확률이기도 하다.
    • 이 값이 0.05미만으로 매우 낮게 나온다면 p-value만큼의 오류 가능성 하에 귀무가설을 기각하고 대립가설을 채택할 수 있는 근거가 된다.
from statsmodels.tsa.stattools import adfuller

def augmented_dickey_fuller_test(timeseries):
    # statsmodels 패키지에서 제공하는 adfuller메소드를 호출
    dftest = adfuller(timeseries, autolag='AIC')
    
    # adfuller메소드가 리턴한 결과를 정리하여 출력
    print('Results of Dickey-Fuller Test : ')
    dfoutput = pd.Series(dftest[0:4], index=['Test Statistic', 'p-value', '#Lags Used', 'Number of Observations Used']
    for key, value in dftest[4].itmes():
    	dfoutput[f'Critical Value {key}'] = value
    
    print(dfoutput)
    

augmented_dickey_fuller_test(ts1)  # 기온 데이터
augmented_dickey_fuller_test(ts2)  # 월별 항공 승객 수 데이터
ts1(기온데이터)ts2(월별 항공 승객 수 데이터)

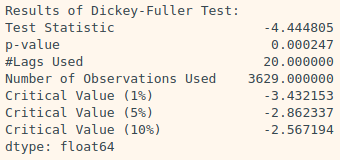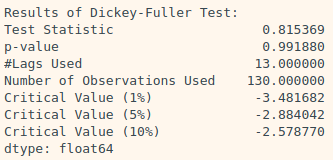→ ts1은 귀무가설은 기각되고, 이 시계열은 안정적 시계열이라는 대립가설이 채택된다.
→ ts2는 시계열이 안정적이지 않다는 귀무가설은 p-value가 거의 1에 가깝게 나타나, 이것이 바로 이 귀무가설이 옳다는 직접적인 증거가 되지는 않지만, 적어도 이 귀무가설을 기각할 수는 없게 되었으므로 이 시계열이 안정적인 시계열이라고 말할 수는 없다.


5. Stationary하게 만들기

안정적이지 않은 시계열데이터를 분석하려면 안정적인 시계열로 만들어줘야 한다.

  • 기존의 시계열데이터를 가공/변형하여 안정적인 특성을 가지도록 함
  • 시계열 분해(Time series decomposition) 기법 적용

로그함수 변환

시간 추이에 따라 분산이 점점 커지고 있다면, 로그함수로 변환을 해주는 것이 도움된다.

ts_log = np.log(ts2)
augmented_dickey_fuller_test(ts_log)

p-value가 0.42로 절반 이상 줄어들었다.


Moving average 제거 - 추세(Trend) 상쇄하기

추세(Trend) - 시계열 데이터에서 시간 추이에 따라 나타나는 평균값 변화
이 변화량을 제거해주려면 거꾸로 Moving Average(rolling mean)를 구해서 ts_log를 빼주면 된다.

moving_avg = ts_log.rolling(window=12).mean()  # moving average구하기
ts_log_moving_avg = ts_log - moving_avg  # 변화량 제거

# window size를 12로 해주었기 때문에 맨 앞의 11개 데이터는
# Moving Average가 계산되지 않으므로 ts_log_moving_avg에 결측치(NaN)가 발생한다.
ts_log_moving_avg.dropna(inplace=True)

plot_rolling_statistics(ts_log_moving_avg)
augmented_dickey_fuller_test(ts_log_moving_avg)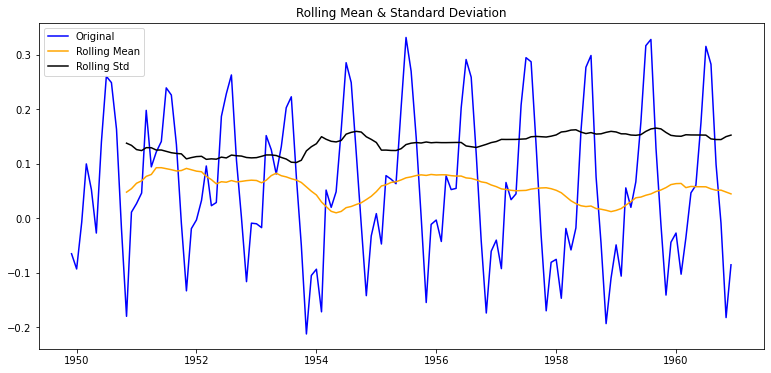

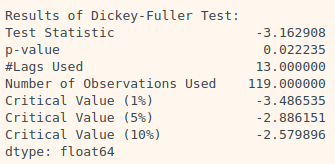
  • p-value가 0.02수준이 되어 이 시계열 데이터가 95% 이상의 신뢰도로 안정적이다라고 말할 수 있다.
  • Moving Average를 계산하는 window size를 6으로 한다면 p-value는 0.18정도가 나온다. 여기서 중요한 것은 주기성을 잘 판단하여 rolling mean의 window size를 넣어줘야 한다는 것이다.

차분(Differencing) - 계절성(Seasonality) 상쇄하기

계절성(Seasonality) - 계절적, 주기적 패턴
차분(Differencing)은 시계열을 한 스텝 앞으로 시프트한 시계열을 원래 시계열에 빼 주는 방법이다. 이렇게 되면 남은 것은 현재 스텝 값 - 직전 스텝 값이 되어 정확히 이번 스텝에서 발생한 변화량을 의미하게 된다. 

ts_log_moving_avg_shift = ts_log_moving_avg.shift()
plt.plot(ts_log_moving_avg, color='blue')
plt.plot(ts_log_moving_avg_shift, color='green')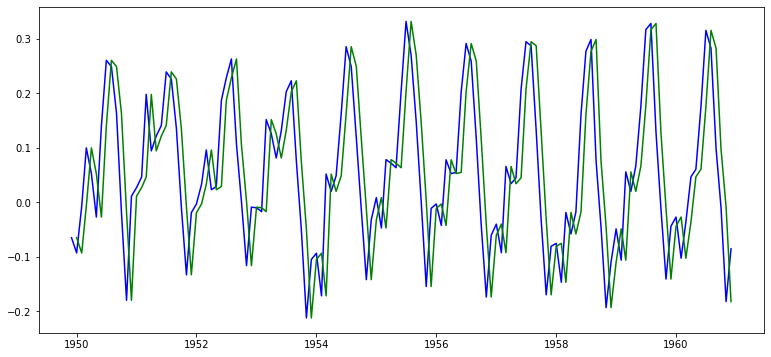

ts_log_moving_avg_diff = ts_log_moving_avg - ts_log_moving_avg_shift
ts_log_moving_avg_diff.dropna(inplace=True)
plt.plot(ts_log_moving_avg_diff)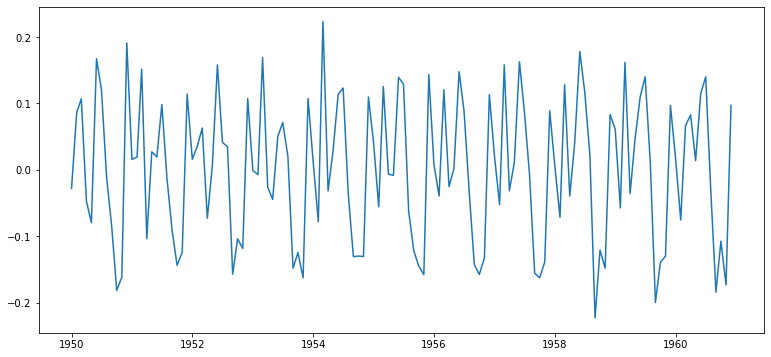

plot_rolling_statistics(ts_log_moving_avg_diff)
augmented_dickey_fuller_test(ts_log_moving_avg_diff)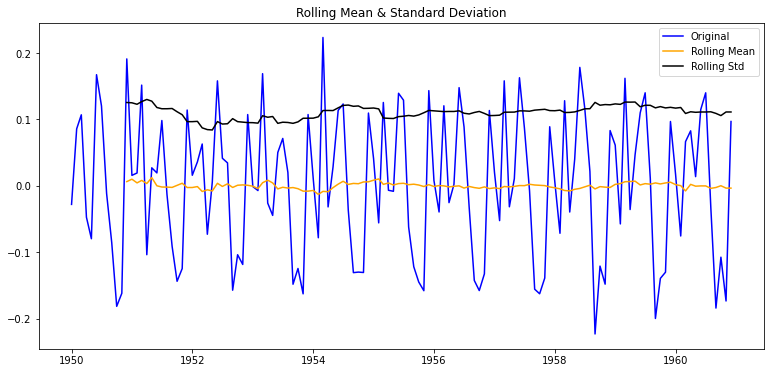

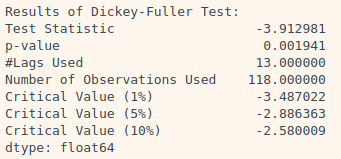
Trend를 제거하고 난 시계열에다가 1차 차분(1st order differencing)을 적용하여 Seasonality 효과를 다소 상쇄한 결과, p-value가 이전의 10% 정도까지로 줄어들었다. 데이터에 따라서는 2차 차분(2nd order differencing, 차분의 차분), 3차 차분(3rd order differencing, 2차 차분의 차분)을 적용하면 더욱 p-value를 낮출 수도 있다.


시계열 분해(Time series decomposition)

seasonal_decompose메소드를 통해 시계열 안에 존재하는 trend, seasonality를 쉽게 분리해낼 수 있다.
Original 시계열에서 Trend와 Seasonality를 제거하고 난 나머지를 Residual이라고 한다. 

from statsmodels.tsa.seasonal import seasonal_decompose
decomposition = seasonal_decompose(ts_log)

trend = decomposition.trend
seasonal = decomposition.seasonal
residual = decomposition.resid

plt.rcParams["figure.figsize"] = (11,6)
plt.subplot(411)
plt.plot(ts_log, label='Original')
plt.legend(loc='best')
plt.subplot(412)
plt.plot(trend, label='Trend')
plt.legend(loc='best')
plt.subplot(413)
plt.plot(seasonal,label='Seasonality')
plt.legend(loc='best')
plt.subplot(414)
plt.plot(residual, label='Residuals')
plt.legend(loc='best')
plt.tight_layout()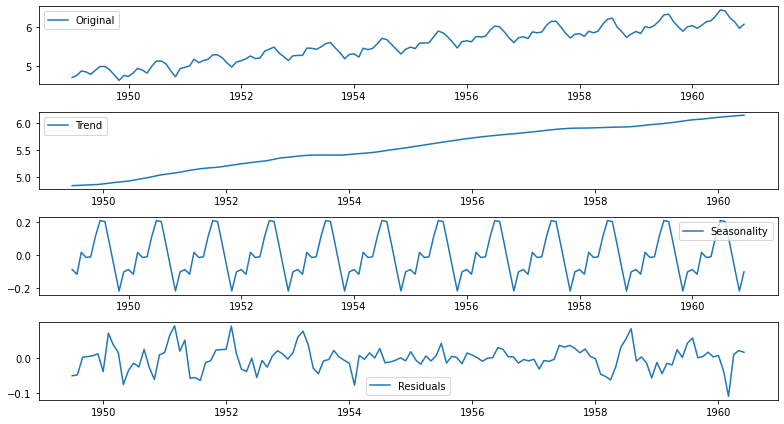

plt.rcParams["figure.figsize"] = (13,6)
plot_rolling_statistics(residual)

residual.dropna(inplace=True)
augmented_dickey_fuller_test(residual)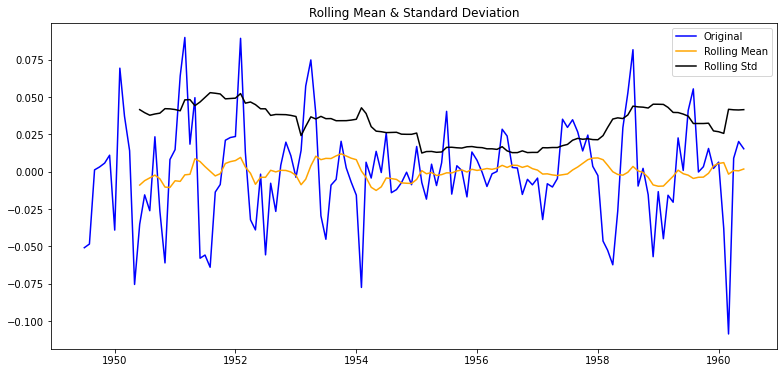

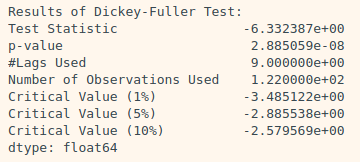
→ Decomposing을 통해 얻어진 Residual은 압도적으로 낮은 p-value를 보인다.





ARIMA

  • Autoregressive Integrated Moving Average
  • AR(Autoregressive) + I(Integrated) + MA(Moving Average)가 합쳐진 모델

모델 정의

AR(Autoregressive, 자기회귀)

  • YtY_t가 이전 p개의 데이터 Yt−1Y_{t-1}, Yt−2Y_{t-2}, ..., Yt−pY_{t-p}의 가중합으로 수렴하는 모델
  • 가중치의 크기가 1보다 작은 Yt−1Y_{t-1}, Yt−2Y_{t-2}, ..., Yt−pY_{t-p}의 가중합으로 수렴하는 자기회귀 모델과 안정적 시계열은 통계학적으로 동치이다.
  • AR은 일반적인 시계열에서 Trend와 Seasonality를 제거한 Residual에 해당하는 부분을 모델링한다고 볼 수 있다.
  • 주식값이 항상 일정한 균형 수준을 유지할 것이라고 예측하는 관점, 오늘은 주식이 올라서 균형을 맞추겠지?라는 기대.

MA(Moving Average, 이동평균)

  • 이동평균(MA)은 YtY_t가 이전 q개의 예측오차값 et−1e_{t-1}, et−2e_{t-2}, ..., et−pe_{t-p}의 가중합으로 수렴한다고 보는 모델
  • MA는 일반적인 시계열에서 Trend에 해당하는 부분을 모델링한다고 볼 수 있다.
  • 예측오차값 et−1e_{t-1}이 +라면 모델 예측보다 관측값이 더 높았다는 뜻이므로, 다음 YtY_t 예측 시에는 예측치를 올려잡게 된다.
  • 주식값은 항상 최근의 증감 패턴이 지속될 것이라고 예측하는 관점, 어제 떨어졌으니 추세적으로 계속 떨어지지 않을까?라는 우려.

I(Integrated, 차분누적)

  • YtY_t이 이전 데이터와 d차 차분의 누적(integration) 합이라고 보는 모델
  • I는 일반적인 시계열에서 Seasonality에 해당하는 부분을 모델링한다고 볼 수 있다.
  • 예를 들어서 d=1이라면 YtY_t는 Yt−1Y_{t-1}과 ΔYt−1\Delta Y_{t-1}의 합으로 보는 것이다.

모수 p, q, d

ARIMA를 활용해서 시계열데이터 예측을 하려면 ARIMA의 모수를 데이터에 맞게 잘 설정해줘야한다.

  • p : 자기회귀 모형(AR)의 시차
  • q : 이동평균 모형(MA)의 시차
  • d : 차분(diffdrence) 횟수

통상적으로 p + q < 2, p * q = 0 인 값들을 사용한다. 이는 p 나 q 중 하나의 값이 0이라는 뜻이다. 이렇게 하는 이유는 실제로 대부분의 시계열 데이터는 자기회귀 모형(AR)이나 이동평균 모형(MA) 중 하나의 경향만을 강하게 띠기 때문이다.

모수 설정 방법

p, q

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

plot_acf(ts_log)   # ACF : Autocorrelation 그래프 그리기
plot_pacf(ts_log)  # PACF : Partial Autocorrelation 그래프 그리기
plt.show()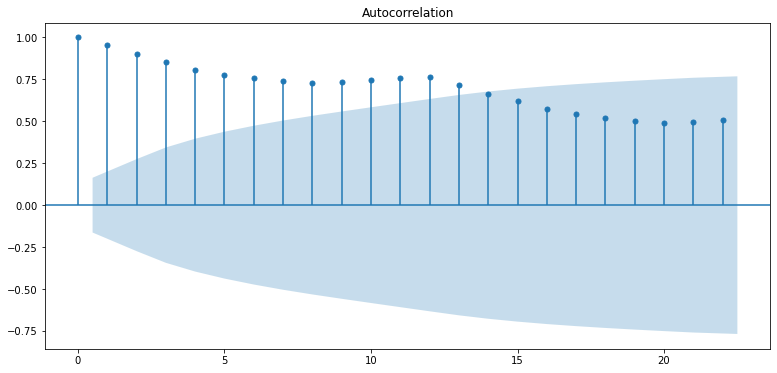

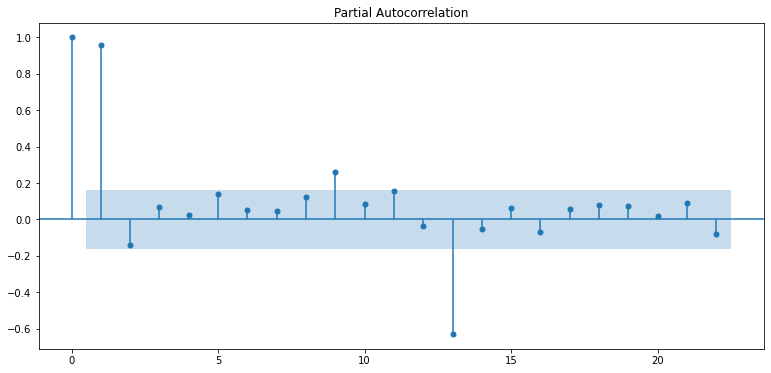
출처 : https://datascienceschool.net

위 그래프 결과로

  • PACF그래프를 보면 p=1이 적합한 것 같다. p가 2 이상인 구간에서 PACF는 거의 0에 가까워지고 있기 때문이다. PACF가 0이라는 의미는 현재 데이터와 p 시점 떨어진 이전의 데이터는 상관도가 0, 즉 아무 상관 없는 데이터이기 때문에 고려할 필요가 없다는 뜻이다.
  • ACF는 점차적으로 감소하고 있어서 AR(1) 모델에 유사한 형태를 보이고 있다. q에 대해서는 적합한 값이 없어 보인다. MA를 고려할 필요가 없다면 q=0으로 둘 수 있다. 하지만 q를 바꿔가면서 확인해보는 것도 좋다.

d

# 1차 차분 구하기
diff_1 = ts_log.diff(periods=1).iloc[1:]
diff_1.plot(title='Difference 1st')

augmented_dickey_fuller_test(diff_1)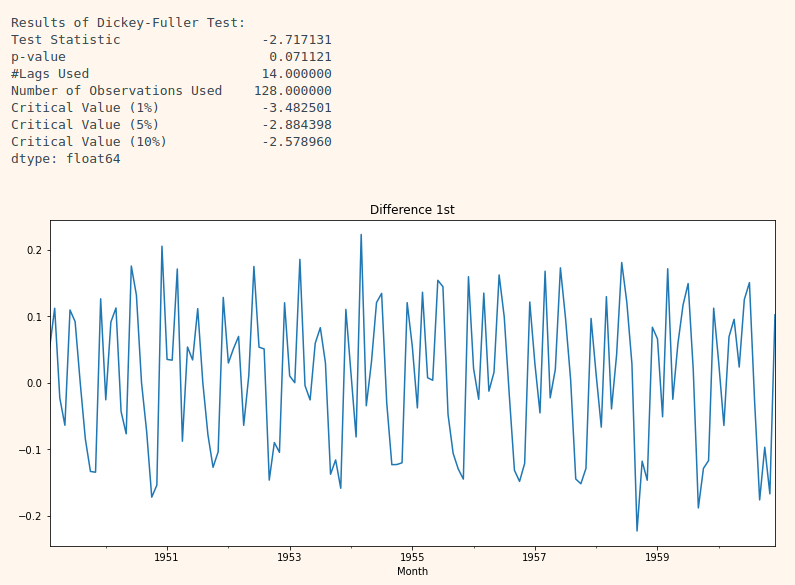

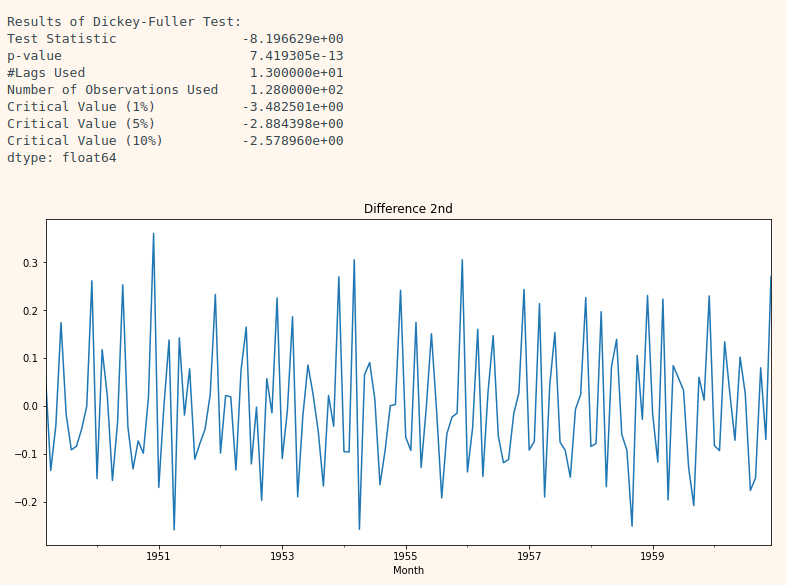
# 2차 차분 구하기
diff_2 = diff_1.diff(periods=1).iloc[1:]
diff_2.plot(title='Difference 2nd')

augmented_dickey_fuller_test(diff_2)

profile
Nam Eun-Ji
한 줄 소개가 자연스러워지는 그날까지
이전 포스트

Tensorflow2 API

다음 포스트

다음에 볼 영화 예측하기

0개의 댓글