Big-O표기법이란 알고리즘을 수행하기 위해 프로세스가 수행해야 하는 연산을 수치화한 것으로, 입력된 N의 크기에 따라 실행되는 조작의 수이다.
문제 해결 단계
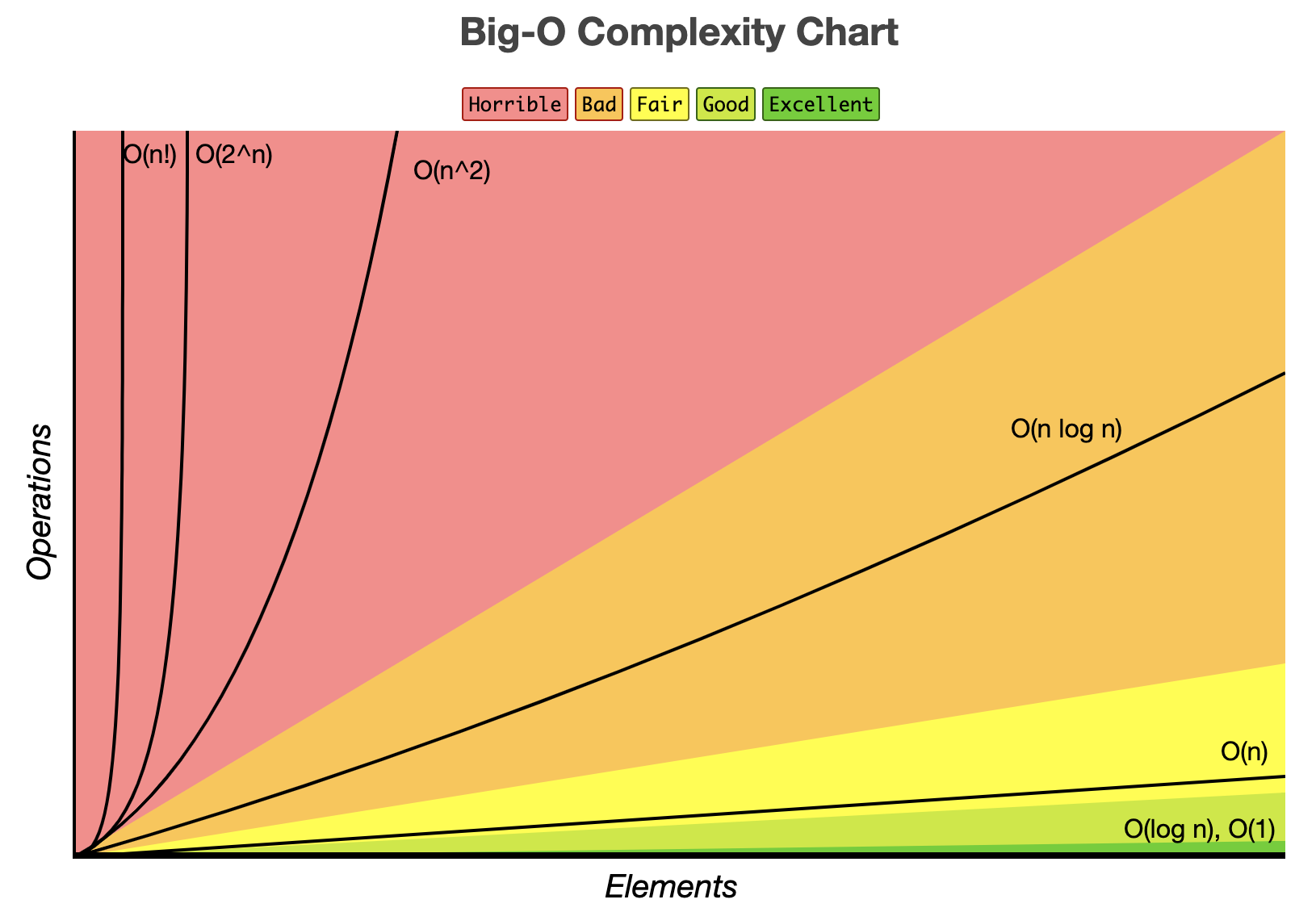
표 아래로 갈 수록 실행시간이 커진다.
| Big-O | 1 | 10 | 100 | |
|---|---|---|---|---|
O(1) | 1 | 1 | 1 | 문제 해결에 오직 한단계만 거친다 |
O(log n) | 0 | 2 | 5 | 문제 해결에 필요한 단계들이 연산마다 특정 요인에 의해 줄어든다 |
O(n) | 1 | 10 | 100 | 문제 해결을 위한 단계의 수와 입력값이 1:1 관계를 가진다 |
O(n log n) | 0 | 20 | 461 | 문제 해결을 위한 단계의 수가 N*(log2N)번만큼의 수행시간을 가진다 |
O(n²) | 1 | 100 | 10000 | 문제 해결을 위한 단계의 수는 입력값 n의 제곱이다 |
O(2ⁿ) | 1 | 1024 | 1267650600228229401496703205376 | |
O(n!) | 1 | 3628800 | 화면에 표현할 수 없음! |
자료구조 시간복잡도
| Data Structures | Search | Insert | Delete |
|---|---|---|---|
Array | O(n) | N/A | N/A |
Sorted Array | O(log n) | O(n) | O(n) |
Linked List | O(n) | O(1) | O(1) |
Doubly Linked List | O(n) | O(1) | O(1) |
Stack | O(n) | O(1) | O(1) |
Hash table | O(1) | O(1) | O(1) |
Binary Search Tree | O(log n) | O(log n) | O(log n) |
B-Tree | O(log n) | O(log n) | O(log n) |
Red-Black tree | O(log n) | O(log n) | O(log n) |
AVL Tree | O(log n) | O(log n) | O(log n) |
이미지 출처 : https://www.bigocheatsheet.com/
한 줄 소개가 자연스러워지는 그날까지