문제 설명
각 edge에 cost가 있는 무방향 그래프에서, 사이클이 없고 edge들의 cost 총합이 최소가 되는 tree를 구하는 문제이다.
그래프 예시

prim 알고리즘
맨 처음에는 아무 정점이나 골라서 MST의 원소로 넣는다. 그 다음 해당 원소의 간선 중 cost가 가장 작은 edge를 골라서 해당 edge, 그리고 이어진 node를 MST의 원소로 추가한다.
MST에 들어간 node들에 이어진 edge들 중에서 싸이클을 만들지 않으면서 최소 cost를 가지는 edge를 찾고, 해당 edge와 이어진 node를 MST의 원소로 추가하는 과정을 반복하면 된다.
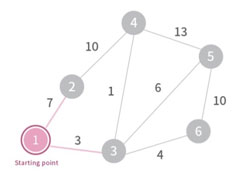
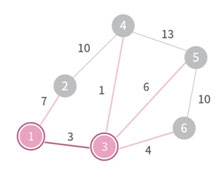
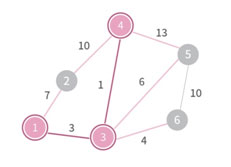
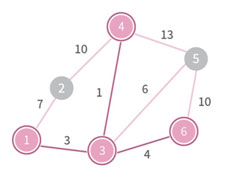
이후 과정은 생략
구현
- Edge.java
package com.company;
public class Edge implements Comparable<Edge>{
public int node1;
public int node2;
public int cost;
public Edge(int node1, int node2, int cost) {
this.node1 = node1;
this.node2 = node2;
this.cost = cost;
}
@Override
public int compareTo(Edge o) {
if(this.cost < o.cost) return -1;
if(this.cost > o.cost) return 1;
return 0;
}
}- Main.java
package com.company;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashSet;
import java.util.PriorityQueue;
public class Main {
public static void prim(Edge[] edges, int startNode, int numOfNodes){
HashSet<Integer> mstNodes = new HashSet<>();
ArrayList<Edge> mstEdges = new ArrayList<>();
PriorityQueue<Edge> candidateEdges = new PriorityQueue<>();
boolean[] edgeUsed = new boolean[edges.length];
Arrays.fill(edgeUsed, false);
mstNodes.add(startNode);
for(int i = 0;i< edges.length;i++){
if(edges[i].node1 == startNode || edges[i].node2 == startNode){
candidateEdges.add(edges[i]);
edgeUsed[i] = true;
}
}
while(mstNodes.size() != numOfNodes){
Edge candidate = candidateEdges.poll();
if(mstNodes.contains(candidate.node1) && mstNodes.contains(candidate.node2))
continue;
mstEdges.add(candidate);
mstNodes.add(candidate.node1);
mstNodes.add(candidate.node2);
for(int i = 0;i<edges.length;i++){
if(edgeUsed[i]) continue;
if(edges[i].node1 == candidate.node1 || edges[i].node1 == candidate.node2
|| edges[i].node2 == candidate.node1 || edges[i].node2 == candidate.node2){
candidateEdges.add(edges[i]);
edgeUsed[i] = true;
}
}
}
for(int i = 0;i<mstEdges.size();i++){
System.out.println(mstEdges.get(i).node1 + ", " + mstEdges.get(i).node2 + " -> " + mstEdges.get(i).cost);
// Edge들 출력
}
}
public static void main(String[] args) {
Edge[] edges = {
new Edge(1, 2, 7),
new Edge(1, 3, 3),
new Edge(2, 4, 10),
new Edge(3, 4, 1),
new Edge(3, 5, 6),
new Edge(3, 6, 4),
new Edge(4, 5, 13),
new Edge(5, 6, 10)
};
int numOfNodes = 6;
int startNode = 1;
prim(edges, startNode, numOfNodes);
}
}시간복잡도
while문이 O(n)번 실행되고, while문이 한 번 실행될 때마다 내부의 for문 실행 횟수도 O(n)이므로 O(n)*O(n) = O(n^2)이다.
Kruskal 알고리즘
모든 Edge들을 cost가 작은 순으로 오름차순 정렬한다. 그리고 각 정점에 번호를 부여한다. 그리고 싸이클을 만들지 않는 edge들 중에서 가장 짧은 edge를 골라 MST에 추가하고, 해당 edge의 각 node들이 속한 그룹들을 하나로 연결한다.(Disjoint Set 알고리즘의 link 함수 이용)
예시
우선 최소 길이인 (3, 4)를 MST에 추가하고 두 노드를 하나의 그룹으로 만든다.
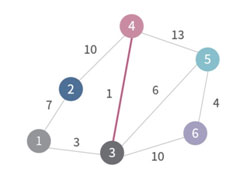
그 다음 최소 길이인 (1, 3)을 MST에 추가하고 1을 3이 속한 그룹에 연결한다.
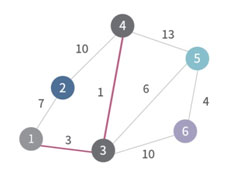
그 다음 최소 길이인 (5, 6)을 연결하고 노드 5와 6을 하나의 그룹으로 만든다.
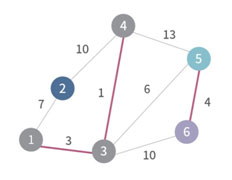
이렇게 싸이클을 만들지 않는 edge들 중에서 최소 cost를 가지는 edge를 MST에 추가하는 과정을 반복한다.
이후 과정은 생략
구현
- Edge.java
- prim 알고리즘에서의 코드와 같다.
- Main.java
package com.company;
import java.util.ArrayList;
import java.util.PriorityQueue;
public class Main {
public static int find(int[] par, int x){
if(par[x] == x) return x;
else return find(par, par[x]);
}
public static void link(int[] par, int x, int y){
par[find(par, y)] = find(par, x);
}
public static void kruskal(Edge[] edges, int startNode, int numOfNodes){
int[] par = new int[numOfNodes + 1];
for(int i = 1;i<=numOfNodes;i++){
par[i] = i;
}
PriorityQueue<Edge> candidateEdges = new PriorityQueue<>();
ArrayList<Edge> mstEdges = new ArrayList<>();
for(Edge e: edges){
candidateEdges.add(e);
}
while(mstEdges.size() < numOfNodes - 1){
Edge candidate = candidateEdges.poll();
if(find(par, candidate.node1) != find(par, candidate.node2)){
// 최고 조상이 같지 않으므로 연결되지 않은 것임
// 이미 연결된 node들을 edge로 연결하면 cycle 만들어짐
link(par, candidate.node1, candidate.node2);
mstEdges.add(candidate);
}
}
for(Edge e: mstEdges){
System.out.println(e.node1 + ", " + e.node2 + " -> " + e.cost);
}
}
public static void main(String[] args) {
Edge[] edges = {
new Edge(1, 2, 7),
new Edge(1, 3, 3),
new Edge(2, 4, 10),
new Edge(3, 4, 1),
new Edge(3, 5, 6),
new Edge(3, 6, 10),
new Edge(4, 5, 13),
new Edge(5, 6, 4)
};
int numOfNodes = 6;
int startNode = 1;
kruskal(edges, startNode, numOfNodes);
}
}