ElasticSearch에서 사용되는 suggest api 관련해서 리서치하다가 내부에서 어떤 알고리즘이 사용되는지 확인하게 되었고, 그 중 가장 기본으로 사용되는 것이 다미레우-레벤슈타인 알고리즘이라는 것을 알게되었다.
이에 대해서 해당 알고리즘이 어떻게 단어간의 편집거리를 구할 수 있게 되는건지 궁금하여 알아보았다.
레벤슈타인 알고리즘?
다미레우 레벤슈타인 알고리즘을 알기 전에 우선 레벤슈타인 알고리즘부터 알아보도록 하자.
레벤슈타인 알고리즘은 두 비교군 간의 삽입, 변경, 삭제에 대한 비용을 계산한다.
계산한 비용이 높을 수록 두 비교군간의 차이가 그만큼 난다는 것을 의미한다.
아주 간단하게 두 단어를 비교해보자.
- a cat
- a abct
1에서 2로 단어를 변경할 때 필요한 비용은 다음과 같이 계산한다.
- a -> a : 0
- -> : 0
- c -> a : 1 (변경)
- a -> b : 1 (변경)
- -> c : 1 (삽입)
- t -> t : 0
자 비용의 총합이 3이므로, 1번의 단어에서 2번의 단어로 변경시에는 3의 비용이 드는 것이다.
자 이걸 이제 계산해보자.
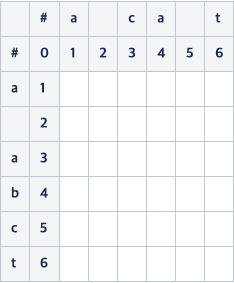
위의 연산을 표로 나타내 본다.
아래와 같은 식을 통해서 한 글자 씩 비교를 하며 연산을 진행한다..
- 비교하는 값이 같으면 왼쪽 대각선 윗 방향의 수를 그대로 가져온다.
- 뭔가 변경이 있었다면 삽입, 삭제, 변경의 값을 아래와 같이 구하여 그 중 최소값을 넣어준다.
- 왼쪽 값에 +1 을 하는 것은 삭제하는 비용
- 위쪽 값에 +1 을 하는 것은 삽입하는 비용
- 왼쪽 윗 대각선 방향에 + 1 하는 것은 변경하는 비용
(편하게 계산하려면 왼쪽, 윗쪽, 왼쪽 윗 대각선중의 최소값에 + 1 을 해주면 된다)
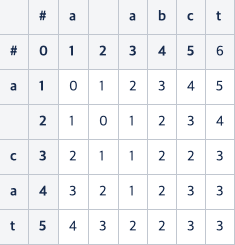
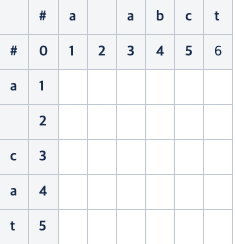
계산은 (a, a), (a, ), (a, a), (a, b), (a, c), (a, t), ( , a), ( , ), ( , a), ... 이렇게 순서대로 진행하면 된다.
계산하면 위와 같이 진행되는데, 가장 마지막 칸에 남은 값이 연산 비용이라고 보면 된다.
위와 같이 3이 나왔다.
알고리즘을 구현하면 아래와 같이 간단하게 구현할 수 있다.
public int levenshteinDistance(String s1, String s2) {
int m = s1.length();
int n = s2.length();
int[][] dp = new int[m + 1][n + 1];
IntStream.rangeClosed(0, s1.length()).forEach(i -> dp[i][0] = i);
IntStream.rangeClosed(0, s2.length()).forEach(j -> dp[0][j] = j);
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
int cost = (s1.charAt(i - 1) == s2.charAt(j - 1)) ? 0 : 1; // 변경의 경우 같은 값이면 0, 다른 값이면 1
dp[i][j] = Math.min(Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1), dp[i - 1][j - 1] + cost); // 위에서 이야기한 최솟값
}
}
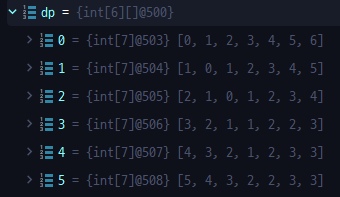
return dp[m][n];
}우리가 위에서 예시로 들었던 두 문자열을 넣으면 아래와 같이 2차원 배열에서 구현되는 것을 확인할 수 있다.
다미레우-레벤슈타인 알고리즘?
우리가 위에서 본 레벤슈타인 알고리즘에 한 가지 규칙을 더 추가한 것이다.
삽입, 변경, 삭제 에 전치(바꿈) 을 추가한 것이다.
아까 위에서 들었던 예시를 통해 다시 알아보면,
a cat이 a abct로 변하는 과정은 다미레우-레벤슈타인 알고리즘에서는 다음과 같다.
- a -> a : 0
- -> : 0
- a <-> c (전치) : 1
- -> b : 1
- t -> t : 0
전치를 통해 비용은 2로 계산된다.
위에서 계산한 것처럼 다미레우-레벤슈타인을 적용하면 다음과 같이 나온다.
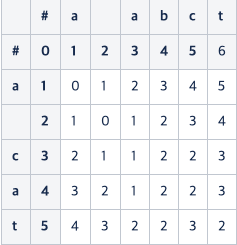
여기에서 전치가 일어나는 부분은 ca를 abc로 변경하는 부분이다.
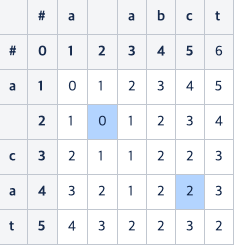
- 전치하기 전의 값 (2, 2) : 0
- a와 c 사이에 추가된 b 연산 : 1
- a와 c의 전치 비용 : 1 - (3, 3) 에서 계산, (4, 5)에서는 계산하지 않음
으로 해서 결국 (4, 5)에 2가 적힌 것을 알 수 있다.
다미레우-레벤슈타인 알고리즘을 구현하는 방법은 위키피디아에 2가지로 나타나있다.
한 가지는 Optimal String Alignment Distance, 다른 한 가지는 Distance with adjacent transpositions 이다.
두 알고리즘의 차이점은 OSA(Optimal String Alignment Distance) 알고리즘은 문자가 두 번 이상 편집되지 않는 조건에서 문자열을 동일하게 만드는 데 필요한 편집 작업 수를 계산하는 반면, Distance with adjacent transpositions 알고리즘은 그러한 제한이 없다는 점이다.
우리가 원하는 다미레우-레벤슈타인은 Distance with Adjacent transpositions 알고리즘이기에 위키피디아에 있는 슈도코드 기반으로 구현해보았다.
public int damerauLevenshteinDistance(String source, String target) {
int lengthOfSource = source.length();
int lengthOfTarget = target.length();
if (lengthOfSource == 0) {
return lengthOfTarget;
}
if (lengthOfTarget == 0) {
return lengthOfSource;
}
int maxLength = Math.max(lengthOfSource, lengthOfTarget);
int[][] distanceMatrix = new int[lengthOfSource + 2][lengthOfTarget + 2];
distanceMatrix[0][0] = maxLength;
// 2차원 배열의 첫번째 열과 행 초기화. 빈 문자열과 대상 문자간의 최대 가능 거리를 나타낸다.
// 첫번째 열 초기화
IntStream.rangeClosed(0, lengthOfSource).forEach(i -> {
distanceMatrix[i + 1][1] = i;
distanceMatrix[i + 1][0] = maxLength;
});
// 첫번째 행 초기화
IntStream.rangeClosed(0, lengthOfTarget).forEach(j -> {
distanceMatrix[1][j + 1] = j;
distanceMatrix[0][j + 1] = maxLength;
});
Map<Character, Integer> previousLocations = new HashMap<>();
for (int i = 0; i < lengthOfSource; ++i) {
previousLocations.put(source.charAt(i), 0);
}
for (int j = 0; j < lengthOfTarget; ++j) {
previousLocations.put(target.charAt(j), 0);
}
for (int i = 1; i <= lengthOfSource; ++i) {
int lastLocationInTarget = 0;
for (int j = 1; j <= lengthOfTarget; ++j) {
int previousLocationInSource = previousLocations.get(target.charAt(j - 1));
int previousLocationInTarget = lastLocationInTarget;
int cost = source.charAt(i - 1) == target.charAt(j - 1) ? 0 : 1;
if (cost == 0) lastLocationInTarget = j;
int substitutionCost = distanceMatrix[i][j] + cost; // 변경
int deletionCost = distanceMatrix[i + 1][j] + 1; // 삭제
int insertionCost = distanceMatrix[i][j + 1] + 1; // 삽입
int transpositionCost = distanceMatrix[previousLocationInSource][previousLocationInTarget] + (i - previousLocationInSource - 1) + 1 + (j - previousLocationInTarget - 1); // 전치
distanceMatrix[i + 1][j + 1] = min(insertionCost, deletionCost, substitutionCost, transpositionCost);
}
previousLocations.put(source.charAt(i - 1), i);
}
return distanceMatrix[lengthOfSource + 1][lengthOfTarget + 1];
}
private int min(int a, int b, int c, int d) {
return Math.min(a, Math.min(b, Math.min(c, d)));
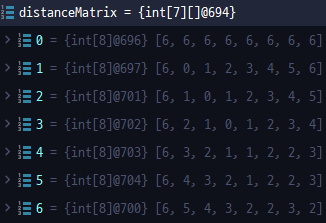
}우리가 위에 그렸던 표와 동일하게 나오는 것을 확인할 수 있다.
참고
https://renuevo.github.io/data-science/levenshtein-distance/
https://www.elastic.co/guide/en/elasticsearch/reference/7.8/search-suggesters.html
https://www.lemoda.net/text-fuzzy/damerau-levenshtein/
https://lovit.github.io/nlp/2018/08/28/levenshtein_hangle/
https://en.wikipedia.org/wiki/Damerau%E2%80%93Levenshtein_distance