소개
여러분이 그래프 관련 문제를 만드는 사람이라고 가정해보겠습니다. 여러분은 아래의 그래프 정보를 어떻게 주실 건가요?
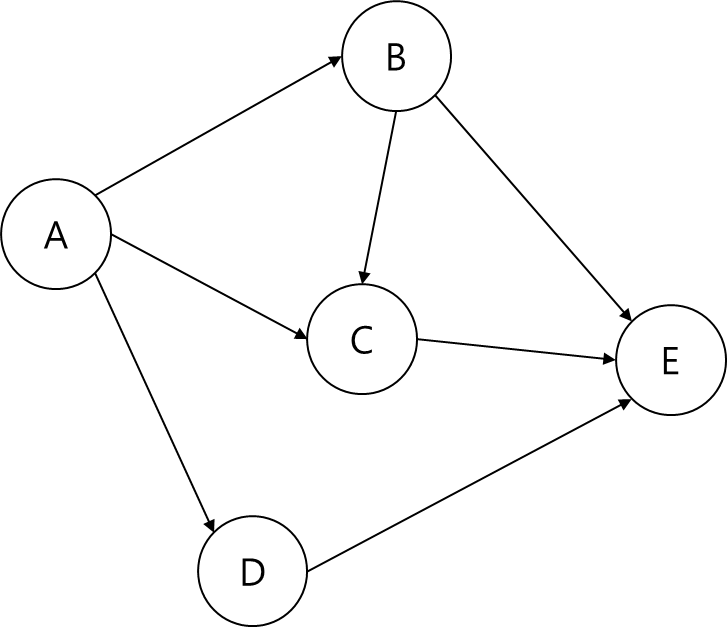
아래와 같은 방식으로 그래프 정보를 줄 수도 있겠지만
A B
A C
A D
B C
B E
C E
D E다음과 같이 줄 수도 있을 것 같습니다.

이렇게 그래프의 연결 관계를 이차원 배열로 나타낸 방식을 인접 행렬이라고 합니다.
특징
자 그러면 인접 행렬의 특징은 무엇이 있을까요?
첫 번째 무방향 그래프의 경우 인접 행렬이 대칭 구조를 이룹니다.
a에서 b로 간다면 b에서 a로 갈 수 있기 때문이죠
참고로 방향이 있는 그래프는 인접 행렬이 비대칭을 이룹니다.
둘. 인접 행렬의 모든 성분의 합은 그래프의 간선 개수와 같습니다.
응? 무방향은 아니지 않아? 하실 수 있지만 무방향 그래프는 a -> b, b -> a가 합쳐져 있어서 실질적으론 2개가 있습니다.
셋. 무방향 그래프인 경우 인접 행렬을 n 승 하면 a에서 b까지 가는 길이 n인 경로의 개수를 알 수 있다.
이건 증명할 여백이 부족하니 생략하겠습니다

장점
자 그럼 인접 행렬의 장점이 무엇이 있을까요?
먼저 두 정점을 연결하는 간선을 조회할 때 O(1)의 시간 복잡도로 찾는 것이 가능하다는 것입니다.
인접 행렬로 정점 A에서 D 사이의 간선을 찾을 때는 [A][D]로 바로 접근해서 찾으면 되기 때문이죠.
단점
그래서 그게 단점이 됩니다.
간선의 수와 무관하게 항상 n^2의 메모리 공간을 차지하고 있기 때문이죠.
그뿐만 아니라 그래프의 모든 간선의 수를 알아내려면 O(n^2)의 시간이 필요합니다.
참고
https://justicehui.github.io/hard-algorithm/2019/06/08/Adj-Matrix-pow/
https://sarah950716.tistory.com/12
https://suyeon96.tistory.com/32
