
오늘은 최소 공통 조상에 대해 알아보겠습니다.
최소 공통 조상이란
최소 공통 조상은 공통 조상 중에 가장 빨리 발견되는 조상입니다.
아래의 그래프로 자세히 알아보겠습니다.
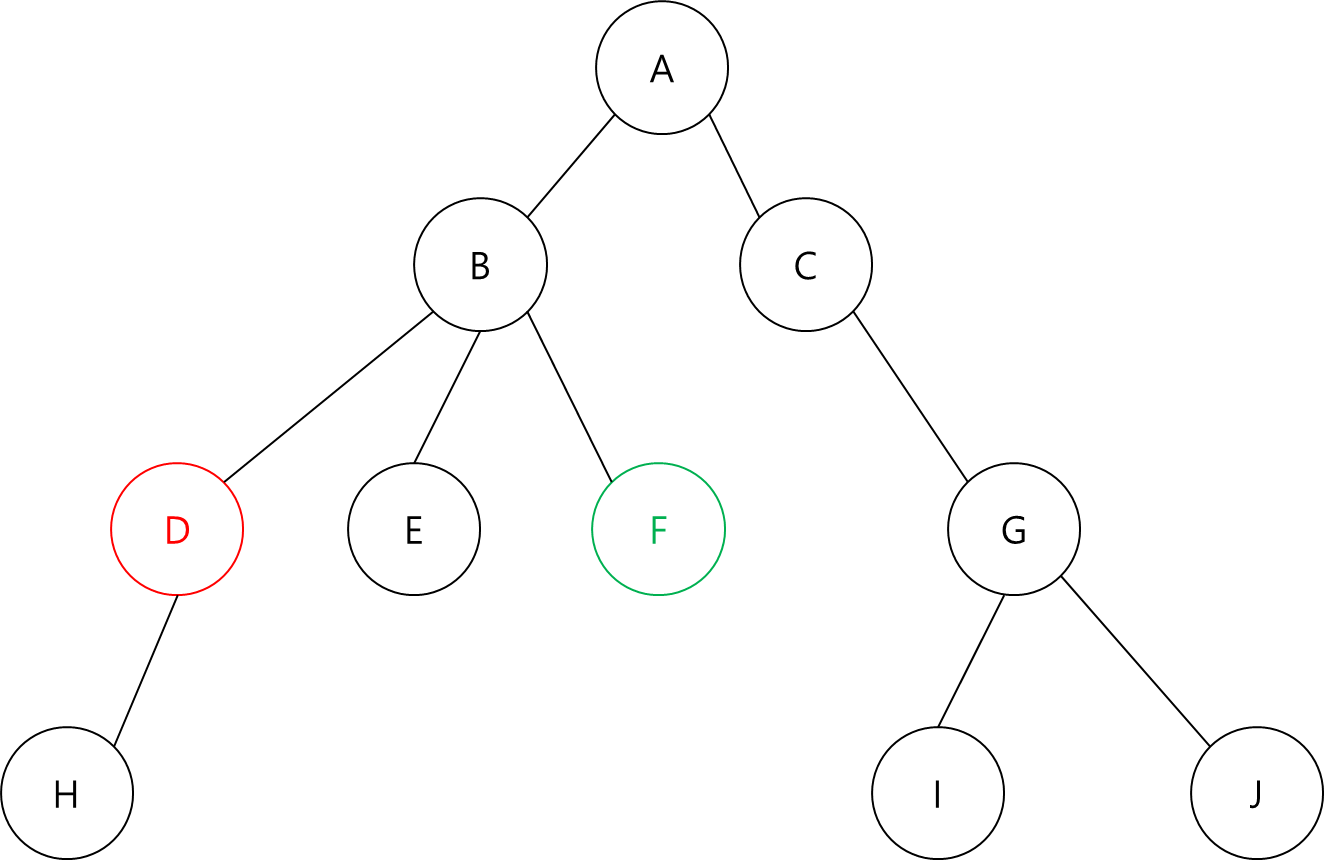
D와 F의 조상이 보이십니까?
D는 B와 A를 조상으로 가지고 있고, F도 B와 A를 조상으로 가지고 있네요.
따라서 D와 F는 B와 A를 공통 조상으로 갖습니다.
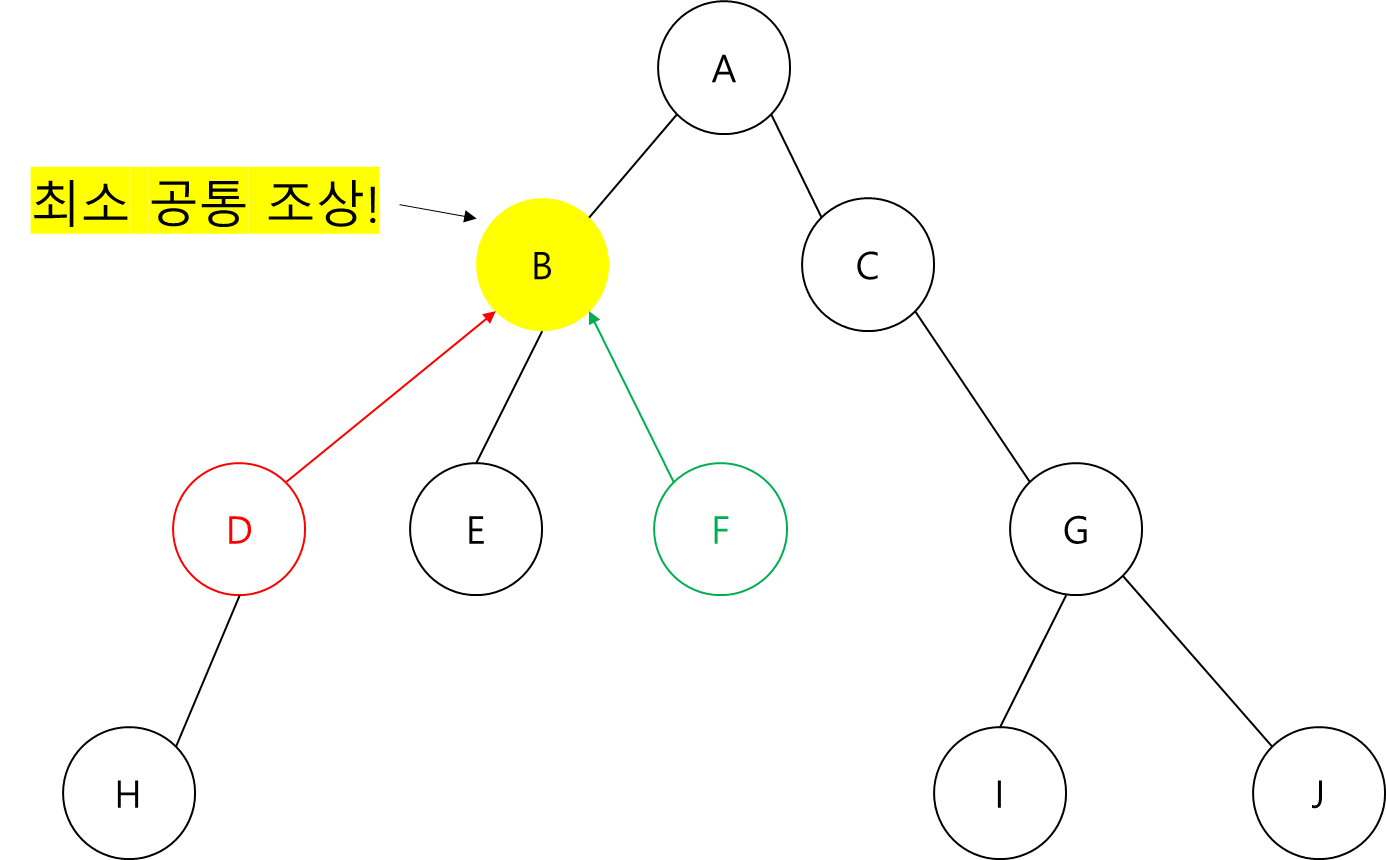
이 중 가장 먼저 발견되는 조상인 B가 최소 공통 조상입니다.
개념은 알겠어. 어떻게 구해?
여러분도 아시는 것처럼 한쪽 정점과 다른 쪽 정점에서 각각 부모로 한 칸씩 올라가며 부모 정점이 같은지 찾으면 됩니다.
아래의 그래프를 통해 자세히 말씀드리겠습니다.
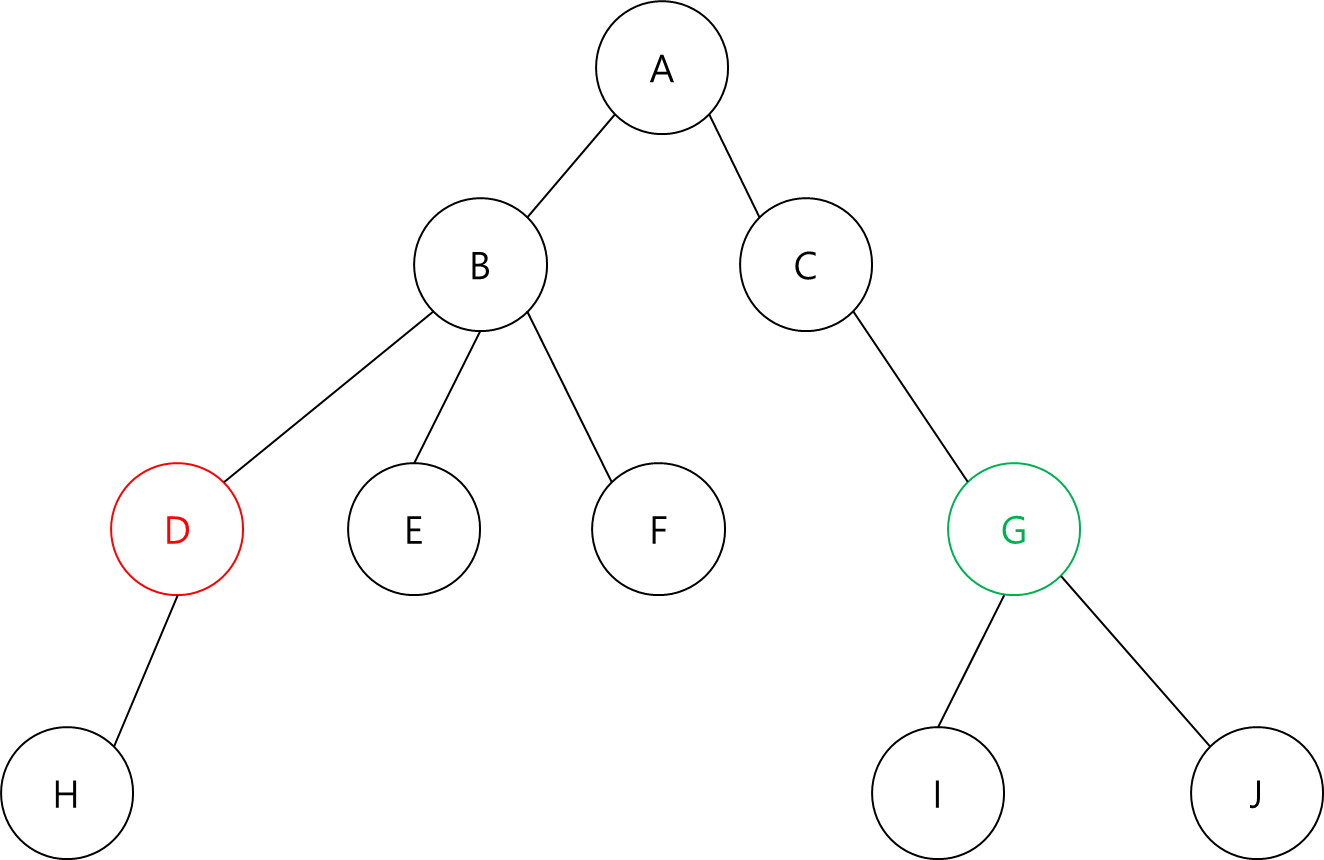
D의 부모(B)와 G의 부모(C)가 같지 않습니다.
따라서 D의 부모인 B와 G의 부모인 C에서 최소 공통 조상을 찾습니다.
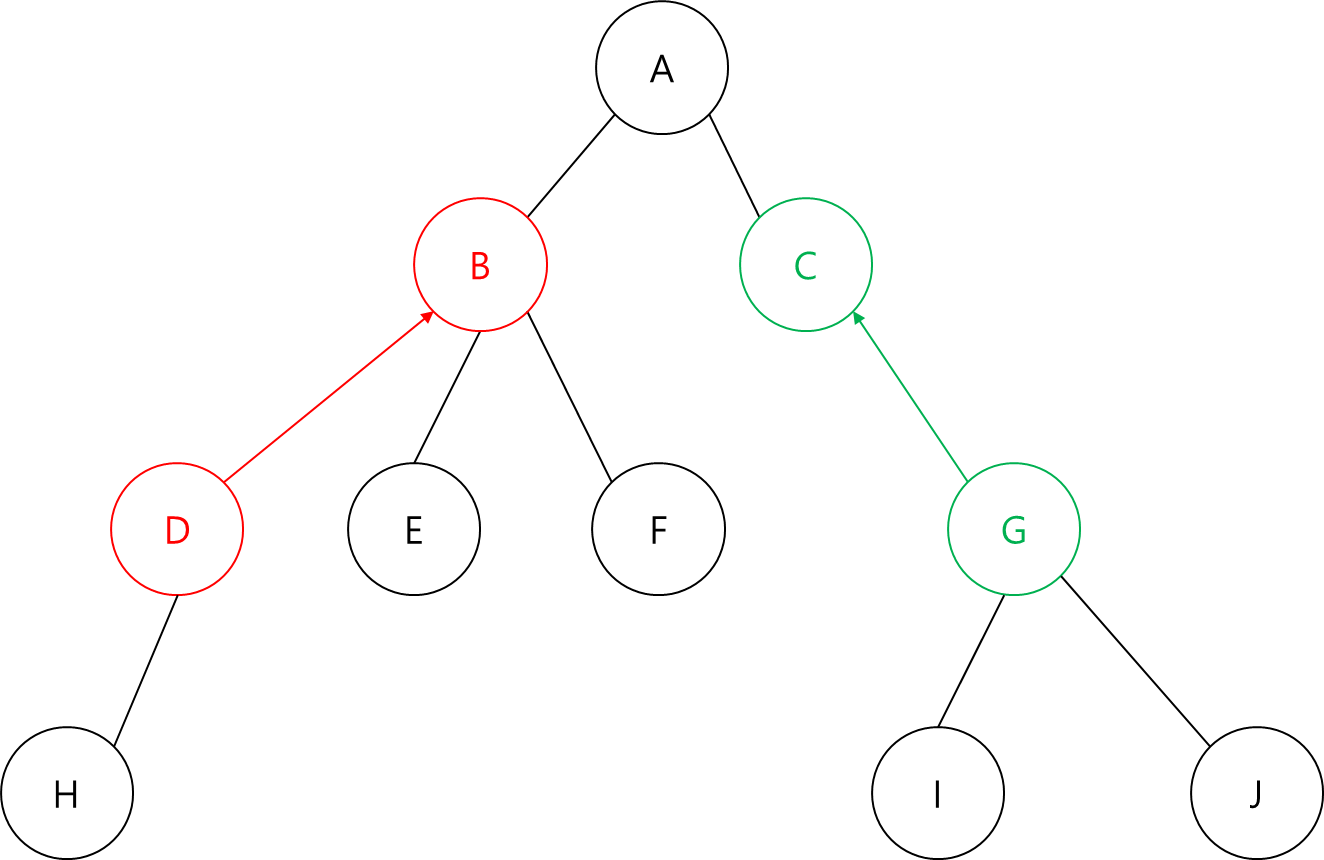
B의 부모(A)와 C의 부모(A)가 같네요.
따라서 D와 G는 A를 최소 공통 조상으로 갖습니다.
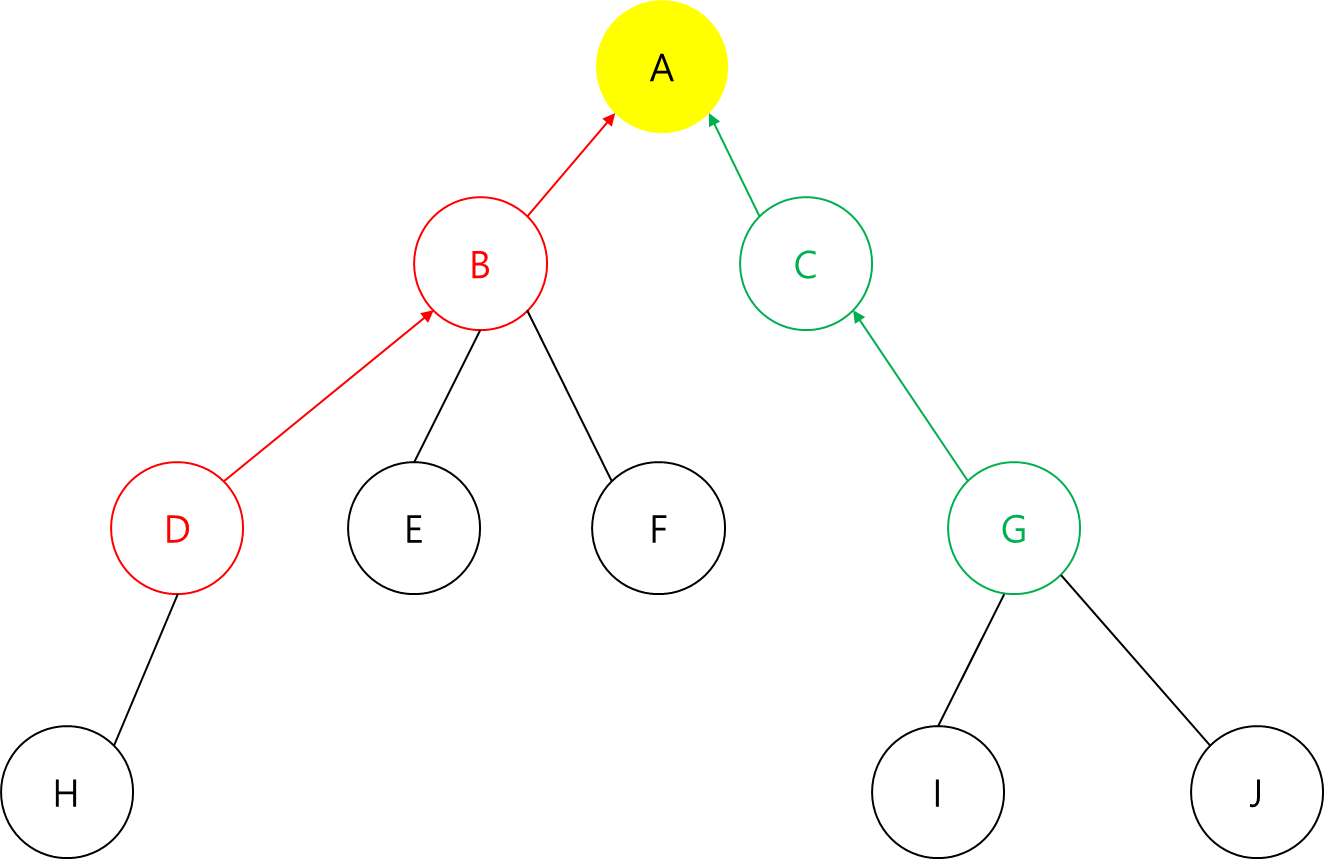
하지만 위의 로직으로 구현하게 된다면 다음과 같은 상황에선 오류를 범합니다.

H와 F의 최소 공통 조상을 찾아보도록 하겠습니다.
H의 부모인 D와 F의 부모인 B가 같지 않습니다.
따라서 D와 B에서 최소 공통 조상을 찾습니다.
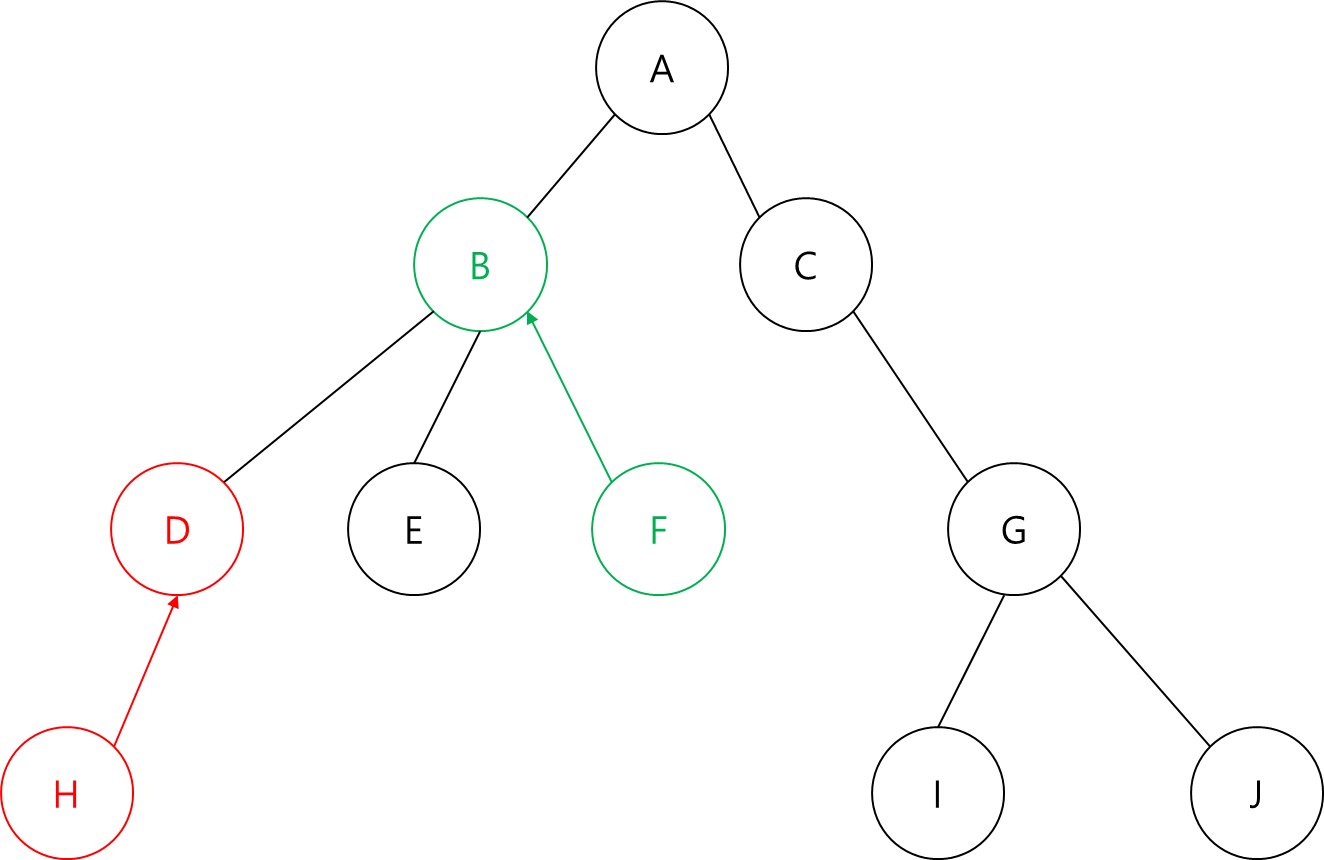
D의 부모인 B와 B의 부모인 A가 같지 않습니다.
따라서 B의 부모와 A의 부모...?
뭔가 이상하지 않나요?
뻔히 H와 F의 최소 공통 조상이 B라는 것을 알지만 위 로직대로라면 B가 나오지 않습니다.
그래서 저희는 사전에 더 깊이 있는 정점을 부모 정점으로 올려 서로 깊이를 맞춰야 합니다.
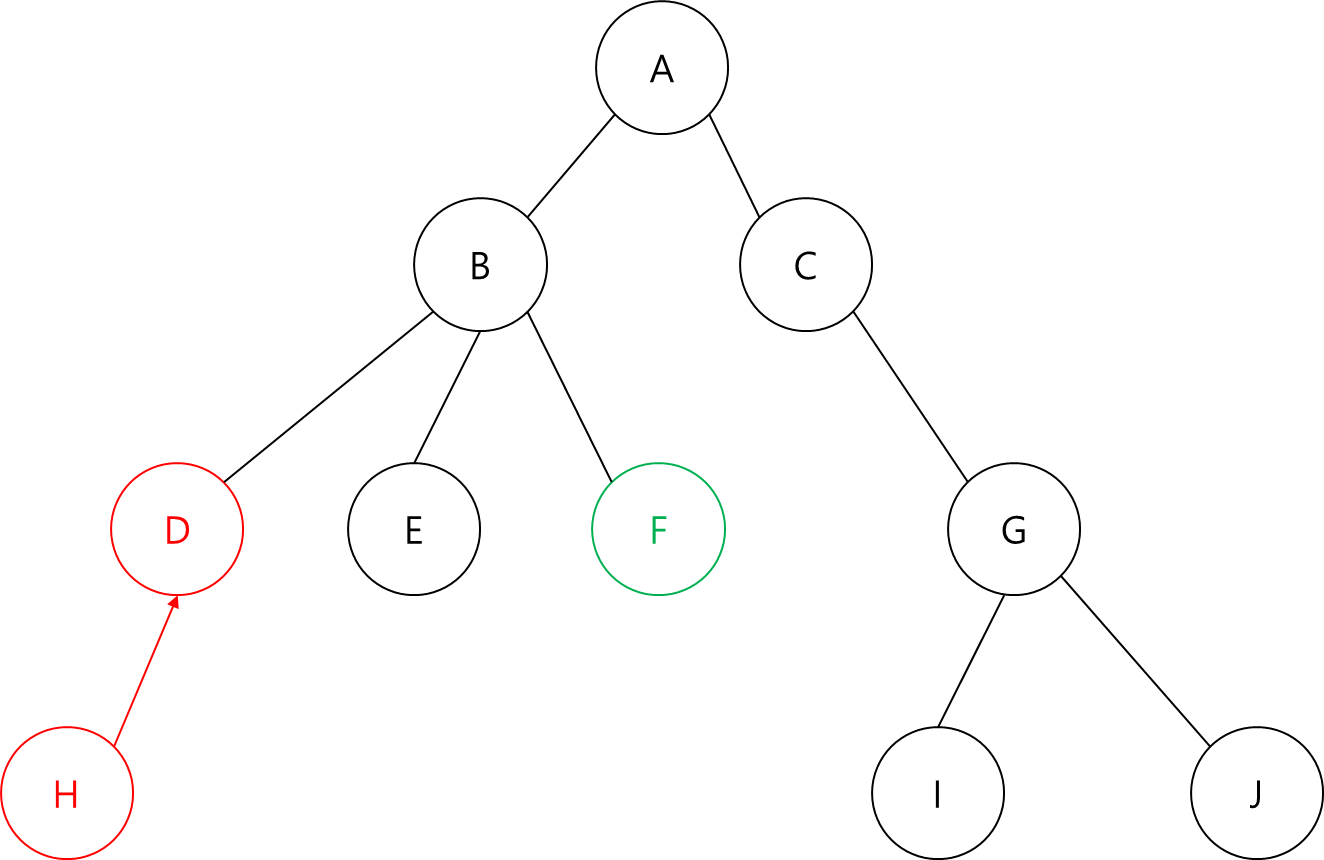
이렇게 더 깊이 있는 정점을 다른 정점의 깊이까지 올라와 같은 깊이에서 탐색해야 올바른 결과를 얻을 수 있습니다.
수도 코드
// 두 정점의 깊이를 같게 만들기
while (depth(deepNode) != depth(notDeepNode)) {
deepNode = parent[deepNode]
}
// 가리키는 정점이 같아질 때까지 거슬러 올라가기
while (deepNode != notDeepNode) {
deepNode = parent[deepNode]
notDeepNode = parent[notDeepNode]
}