그리디 알고리즘
현재 상황에서 지금 당장 좋은 것만 고르는 방법
-
일반적인 그리디 알고리즘은 문제를 풀기 위한 최소한의 아이디어를 떠올릴 수 있는 능력 요구
-
정당성 분석이 중요!
단순히 가장 좋아 보이는 것을 반복적으로 선택해도 최적의 해를 구할 수 있는지 검토
예시
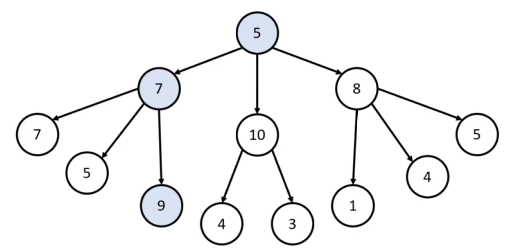
루트 노드부터 시작하여 거쳐 가는 노드 값을 최대 합으로 만들고 싶을 때 최적의 해는?

그리디 알고리즘은 매 상황에서 가장 큰 값만 고른다.
일반적으로 그리디 알고리즘은 최적의 해를 보장할 수 없을 때가 많다.
하지만 코테에서 대부분 그리디는 탐욕법으로 얻은 해가 최적의 해가 되는 상황에서 이를 추론할 수 있어야 풀리도록 출제
대표 문제
카운터에 거스름돈으로 사용할 500원, 100원, 50원, 10원 동전이 무한히 존재한다고 가정한다. 손님에게 거슬러 주어야 할 돈이 N원 일 때 거슬러 주어야 할 동전의 최소 개수를 구하세요. 단, N은 항상 10의 배수.
문제 해결 아이디어
단순히 가장 큰 화폐 단위부터 거슬러 준다.
정당성 분석
큰 단위가 항상 작은 단위의 배수이므로 작은 단위 동전들을 종합해 다른 해가 나올 수 없기 때문
만약 화폐 단위가 500원, 400원, 100원이라면 800원을 거슬러줘야할 때 그리디로는 500원 1개, 100원 3개가 나오지만 사실은 400원 2개가 최적의 해다.
이처럼 그리디 알고리즘에서는 최소한의 아이디어를 떠올리고 정당한지 검토할 수 있어야 한다.
시간 복잡도 분석
화폐의 종류가 K라고 할 때, 화폐의 종류만큼 반복하므로 시간복잡도는 이다.
그리디 유형 문제 풀이
문제 1) 1이 될 때까지
문제

어떠한 수 N이 1이 될 때까지 다음의 두 과정 중 하나를 반복적으로 선택하여 수행. 단, 두번째 연산은 N이 K로 나누어 떨어질 때만 선택 가능.
- N에서 1을 뺀다.
- N을 K로 나눈다.
N이 1이 될 때까지 1번 혹은 2번의 과정을 수행해야하는 최소 횟수는?
N(1 <= N <= 100000), K(2 <= K <= 100000)
예시
N = 17, K = 4
1번 과정을 한 번 수행하면 N은 16
이후에 2번 과정 두 번 수행하면 N은 1
✅ 전체 과정 실행 횟수: 3
문제 해결 아이디어
주어진 N에 대해 최대한 많이 나누기를 수행하면 된다.
N의 값을 줄일 때 2 이상의 수로 나누는 작업이 1을 빼는 작업보다 수를 훨씬 많이 줄일 수 있기 때문.
정당성 분석
가능하면 최대한 많이 나누는 작업이 최적의 해를 보장할 수 있을까?
N이 아무리 큰 수여도, K가 2 이상이기 때문에 나누는 것이 기하급수적으로 빠르게 줄일 수 있다.
또한 N은 항상 1에 도달하게 된다.
풀이
if문으로 나누어 떨어지면 나누고 그렇지 않으면 1을 빼는 방법도 있지만 한번에 나누어 떨어지는 값을 만든다음에 나눠주는 방법이 더 효율적이다.
n, k = map(int, input().split())
count = 0
while True:
# n이 k로 나누어 떨어지는 수가 될 때까지 빼기
target = (n // k) * k
count += (n - target)
n = target
# n이 k로 더 이상 나눌 수 없을 때 탈출
if n < k:
break
# k로 나누기
n //= k
count += 1
# 남은 수에서 1씩 빼기
count += (n - 1)
print(count)✅ 시간 복잡도:

