정규화
정규화란 함수적 종속성 등의 이론을 이용하여
잘못된 스키마를 더 작은 속성의 세트로 쪼개어 바람직한 스키마로 만들어 가는 과정
- 하나의 종속성이 하나의 릴레이션에 표현될 수 있도록 분해해가는 과정이라 할 수 있다.
- 정규형의 차수가 높아질 수록 만족시켜야할 제약조건이 늘어간다.
목적
- 불필요한 데이터(redundancy) 즉 중복된 데이터를 제거.
- 삽입/갱신/삭제 시 발생할 수 있는 각종 이상현상(Anamolies)들을 방지.
- "논리적"로 데이터를 저장 - 데이터 테이블의 구성이 논리적이고 직관적
이상현상(Anamlies)
정규화를 거치지 않으면 데이터베이스 내에 데이터들이 불필요하게 중복되어
릴레이션 조작시 예기치 못한 현상이 발생한다.
삽입이상릴레이션에 데이터를 삽입살때 의도와는 상관없이 원하지 않은 값들도 함께 삽입된다.
예)
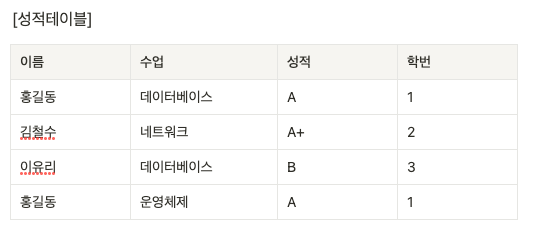
학생과 과목에 대한 성적테이블이 있는데 새로운 학생이 아직 수업을 등록하지 못해 성적이 없다면
이 학생에 대한 정보를 추가할 수 없다.
갱신이상릴레이션에서 튜플에 있는 속성값을 갱신할 때 일부 튜플의 정보만 갱신되어 모순이 생기는 현상
예)
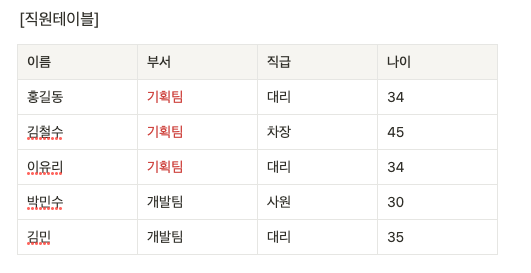
직원 테이블이 있고 각 지원이 속한 부서 정보가 포함된 경우,
하나의 부서 이름을 변경하려면 그 해당 부서에 속한 모든 직원의 행을 수정해야한다.
하나만 변경하면 모순이 생긴다.
삭제이상릴레이션에서 한 튜플을 삭제할 때 의도와 상관없은 값들도 함께 삭제되는
연쇄가 일어나는 현상예)
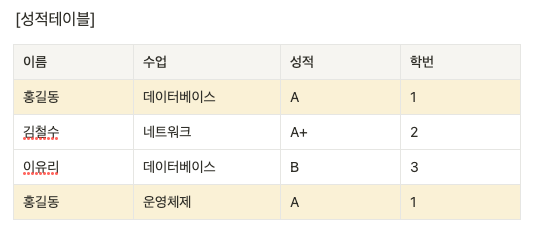
성적 테이블에서 특정학생이 수강한 모든 과목의 데이터를 삭제하면
해당 학생에 대한 정보(학번)까지 모두 사라진다.
성능
정규화 수준이 높을 수록 유연한 데이터 구축이 가능하고 데이터 정확성이 높아지지만
물리적 접근이 복잡하고 너무 많은 조인으로 이해 조회 성능이 저하된다.
제1정규형
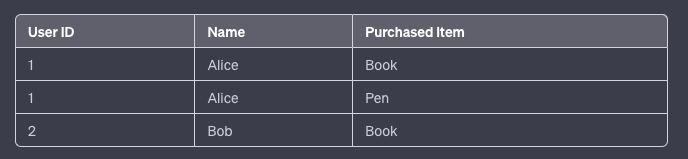
릴레이션에 속한 모든
도메인은 원자값으로만 되어있는 정규형
각각의 행은 유일한 식별자(기본키)를 가져야한다.
같은 테이블 내애서 중복된 행이 없어야 한다.
제2정규형
릴레이션 R이 제1정규형이고
기본키가 아닌 모든 속성이
기본키에 대하여완전 함수적 종속을 만족하는 정규형
완전 함수적 종속이란 기본키의 부분집합이 결정자가 되어선 안된다는 것을 의미한다.
즉, 기본키 중에 특정 컬럼에만 종속된 컬럼이 없어야 된다.<수강> 릴레이션이 (학번,과목명,성적)으로 되어있고
(학번, 과목명) 이 기본키 일때,
성적은 (학번, 과목명) 이 같은 경우에만 항상 같은 성적이 나온다.
이 경우를완전 함수적 종속이라고 한다.부분 함수적 종속은
기본 키의 일부에 의해서 결정이 되는 속성을 말한다.
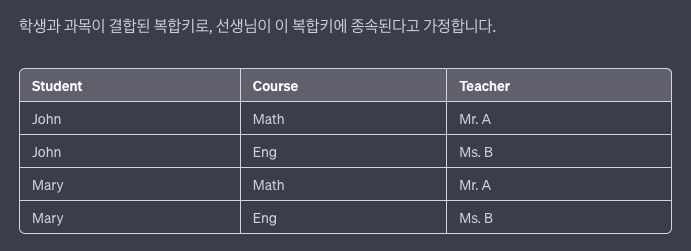
예를 들어 '학년'은 '학번' 속성만으로 알 수 있다.위 테이블에서 복합키는 (Student, Course)이며, Teacher는 복합키에 함수적 종속이다.
즉, 학생과 과목을 알면 선생님을 알 수 있습니다.그러나, 이 테이블은 2NF를 만족하지 않는다.
Teacher(선생님)은 Course(과목)에만 부분적으로 종속되기 때문이다.
결정자란 속성간의 종속성을 규명할때 기준이 되는 값이다.
종속자란결정자에 의해 값이 정해지는 값을 의미한다.예)
'학번' 에 따라 '이름' 이 정해질때
'학번' 은 결정자가 되고 '이름'은 종속자가 된다.
제3정규형
릴레이션 R이 제2정규형이고
기본키가 아닌 모든 속성이
기본키에 대하여이행적 종속을 만족하는 정규형
이행적 종속
A->B, B->C 일때 A->C가 성립되는 것을 의미한다.
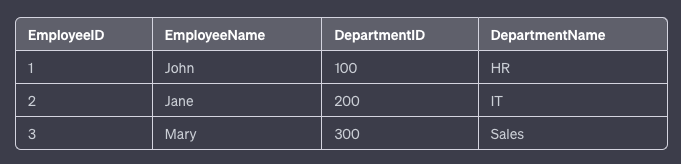
즉, 기본키 이외의 다른 컬럼을 결정할 수 없다는 것을 의미한다.위 테이블에서
DepartmentName은DepartmentID에 이행적으로 종속적이다.
즉,EmployeeID->DepartmentID->DepartmentName의 관계가 성립하므로,
이는 제3정규형을 만족하지 않는다.
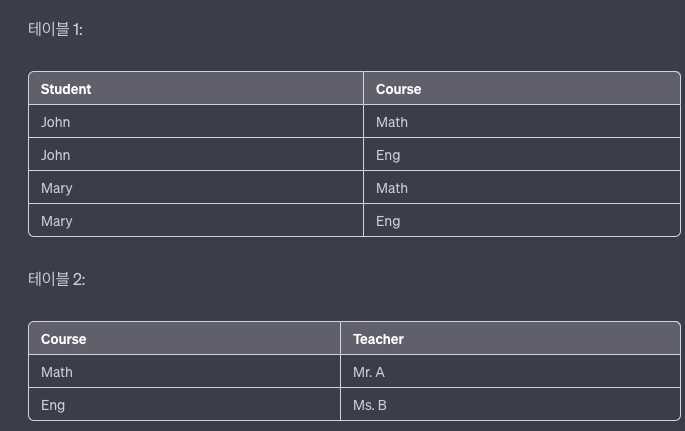
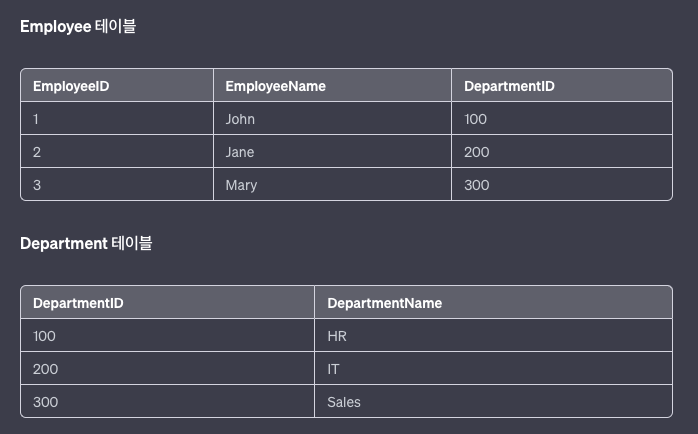
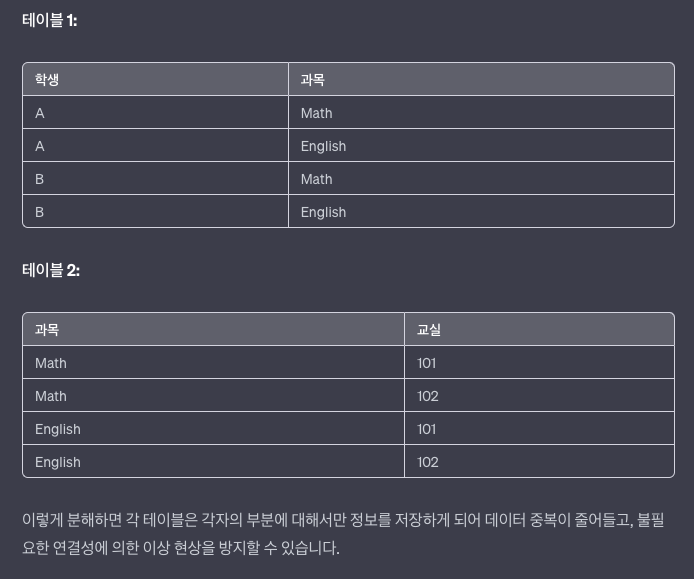
이를 제3정규형에 맞게 조정하기 위해 두 개의 테이블로 분리할 수 있습니다.
BCNF(Boyce-Codd) 정규형
릴레이션 R이 제3정규형이고
결정자(함수 종속성에서 왼쪽)가 모두
후보키가 되어 테이블을 분리하는 것
즉결정자이면서 후보키가 아닌 것을 제거하는 것이다.
후보키란 기본키가 될 수 있는 속성을 말한다.
- 유일성: 중복된 값을 가질 수 없다. 각 행을 유일하게 식별할 수 있어야 한다.
- 최소성 : 후보키를 구성하는 속성은 반드시 최소여야한다.
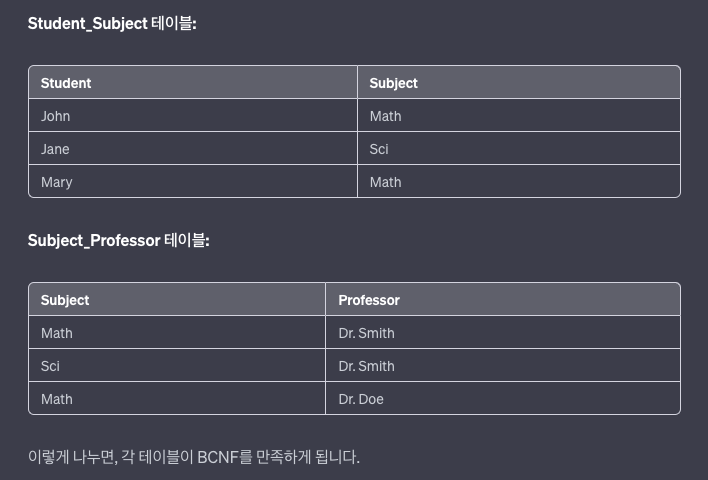
위의 테이블에서 기본키는(Student, Subject)이다.
이 기본키(Student, Subject)은 'Professor'을 결정짓고,
'Subject'은 'Professor'을 결정짓는다.하지만 여기서 'Subject'은 결정자지만 후보키가 아니다는 문제가 있다.
이 경우, 만약 'Subject'이 변경되면, 'Professor'도 변경해야 갱신 문제가 발생할 수 있다.이런 문제점을 해결하기 위해서 BCNF 정규화를 한다.
BCNF 제약 조건
- 키가 아닌 속성은 각 키에 대하여 완전 종속해야한다.
- 키가 아닌 속성은 그 자신이 부분적으로 들어가 있지 않은 모든 키에 대해여 완전 종속해야한다.
- 어떤 속성도 키가 아닌 속성에 대해서는 완전 종속할 수 없다.
제4정규형
릴레이션 R에 다치 종속 A->>B 가 성립하는 경우
모든 속성이 A에 함수적 종속 관계를 만족하는 정규형
다치 종속
A,B,C 3개의 속성을 가진 릴레이션 R 에서
어떤 복합 속성(A,C)에 대응하는 B값의 집합이 A 값에만 종속되고
C 값에는 무관하면 B는 A에 다치 종속이라고 하고 A->>B 라고 표현한다.즉, 한 특성이 다른 특성에 의해 종속되어 있는데,
이런 종속관계가 기본키에만 의존하지 않고 다른 특성에도 의존하는 관계를 말한다.
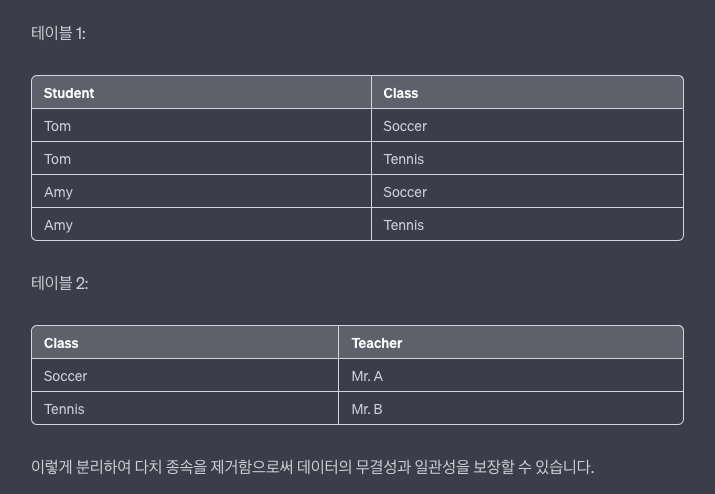
위 테이블에서 기본키는 "Student"와 "Class" 이며
"Student"와 "Class", "Student"와 "Teacher" 사이에 다치 종속이 있다.
예를 들어, Tom 학생이 Soccer를 선택하면 그의 선생님은 반드시 Mr. A가 되고,
Tennis를 선택하면 그의 선생님이 Mr. B가 됩니다.
제5정규형
릴레이션 R이 모든 조인 종속이 R의 후보키를 통해서만 성립되는 정규형이다.
조인 종속
어떤 릴레이션의 R의 속성에 대한 부분집합 A,B, ... C 가 있다고 가정하자
이때 만약 릴레이션 R이 자신의 프로젝션 A,B, ..., C를 모두 조인한 결과가
자신과 동일한 경우 조인 종속을 만족한다고 한다.