[백준] 1261번: 알고스팟

문제

알고스팟 운영진이 모두 미로에 갇혔다. 미로는 NM 크기이며, 총 11크기의 방으로 이루어져 있다. 미로는 빈 방 또는 벽으로 이루어져 있고, 빈 방은 자유롭게 다닐 수 있지만, 벽은 부수지 않으면 이동할 수 없다.

알고스팟 운영진은 여러명이지만, 항상 모두 같은 방에 있어야 한다. 즉, 여러 명이 다른 방에 있을 수는 없다. 어떤 방에서 이동할 수 있는 방은 상하좌우로 인접한 빈 방이다. 즉, 현재 운영진이 (x, y)에 있을 때, 이동할 수 있는 방은 (x+1, y), (x, y+1), (x-1, y), (x, y-1) 이다. 단, 미로의 밖으로 이동 할 수는 없다.

벽은 평소에는 이동할 수 없지만, 알고스팟의 무기 AOJ를 이용해 벽을 부수어 버릴 수 있다. 벽을 부수면, 빈 방과 동일한 방으로 변한다.

만약 이 문제가 알고스팟에 있다면, 운영진들은 궁극의 무기 sudo를 이용해 벽을 한 번에 다 없애버릴 수 있지만, 안타깝게도 이 문제는 Baekjoon Online Judge에 수록되어 있기 때문에, sudo를 사용할 수 없다.

현재 (1, 1)에 있는 알고스팟 운영진이 (N, M)으로 이동하려면 벽을 최소 몇 개 부수어야 하는지 구하는 프로그램을 작성하시오.

입력

첫째 줄에 미로의 크기를 나타내는 가로 크기 M, 세로 크기 N (1 ≤ N, M ≤ 100)이 주어진다. 다음 N개의 줄에는 미로의 상태를 나타내는 숫자 0과 1이 주어진다. 0은 빈 방을 의미하고, 1은 벽을 의미한다.

(1, 1)과 (N, M)은 항상 뚫려있다.

출력

첫째 줄에 알고스팟 운영진이 (N, M)으로 이동하기 위해 벽을 최소 몇 개 부수어야 하는지 출력한다.

입출력 예제

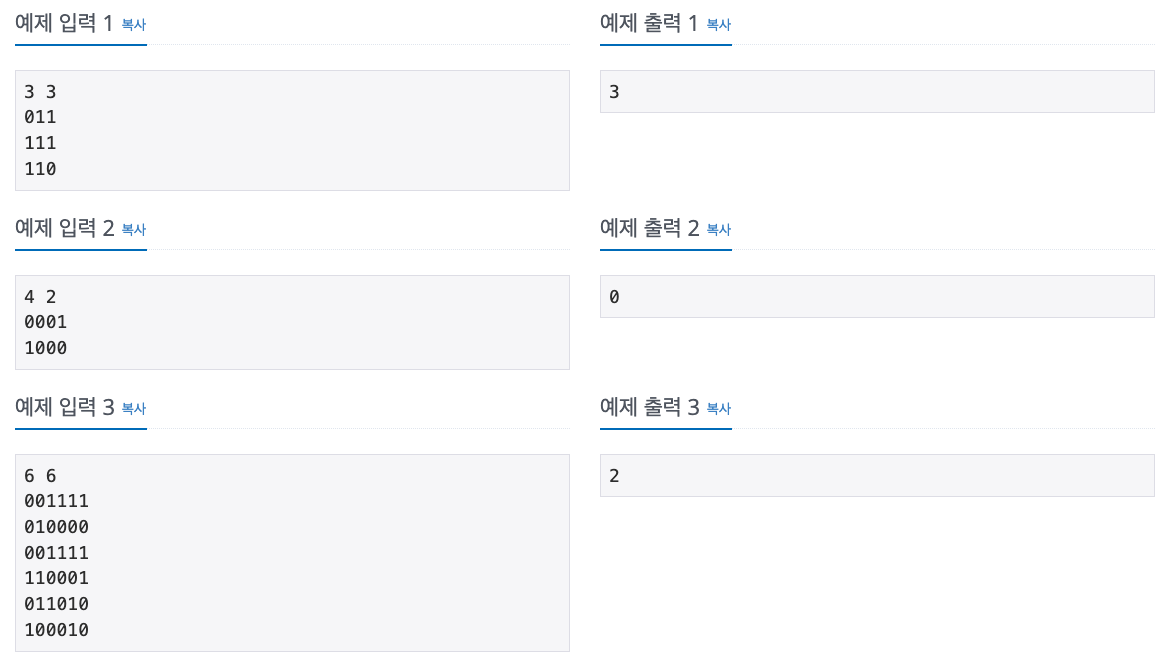
풀이

heap 다익스트라를 활용한 풀이
방문한 칸을 heap(방문 예정 저장공간)에 넣는다.
heap을 사용하는 이유는 벽의 부순 개수가 최소가 되어야하기 때문에
현재 칸은 이전에 방문한 칸들에서 부순 벽의 개수보다 같거나 커야한다.
그렇게 때문에 방문 예정 저장공간에서 부순 벽의 개수가 작은 것부터 꺼내야한다.

import sys
import heapq  # heapq 모듈은 우선순위 큐를 제공

# 테스트 데이터를 읽기 위한 설정
sys.stdin = open("data.txt", 'r')
input = sys.stdin.readline

# N은 열의 수, M은 행의 수, 입력 받기
N, M = map(int, input().split(" "))
# 2차원 배열로 미로 구조를 저장
graph = [list(map(int, input().rstrip())) for _ in range(M)]

def solution(N, M, graph):
    # 미로 내 각 위치의 방문 여부를 저장할 2차원 배열
    visited = [[False] * N for _ in range(M)]
    # 우선순위 큐에 시작점과 비용을 넣는다 (부순 벽의 개수, y좌표, x좌표)
    heap = [(0, 0, 0)]
    # 시작점 방문 처리
    visited[0][0] = True

    # 상하좌우 이동을 위한 좌표 설정
    dy = [-1, 1, 0, 0]
    dx = [0, 0, -1, 1]
   
    # 우선순위 큐가 빌 때까지 탐색
    while heap:
        # 부순 벽의 개수와 현재 좌표를 가져온다
        count, y, x = heapq.heappop(heap)

        # (N, M)에 도달하면 부순 벽의 개수를 출력하고 함수 종료
        if y == M - 1 and x == N - 1:
            print(count)
            return

        # 4방향으로 이동
        for i in range(4):
            ny = y + dy[i]
            nx = x + dx[i]

            # 미로 범위 안에 있고 방문하지 않았다면
            if 0 <= ny < M and 0 <= nx < N and not visited[ny][nx]:
                # 벽이면 부수고 이동, 부순 벽의 개수를 1 증가
                if graph[ny][nx] == 1:
                    heapq.heappush(heap, (count + 1, ny, nx))
                # 빈 방이면 부수지 않고 이동, 부순 벽의 개수는 그대로
                else:
                    heapq.heappush(heap, (count, ny, nx))
                # 해당 위치 방문 처리
                visited[ny][nx] = True

# 함수 호출
solution(N, M, graph)