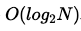[백준] 1654번: 랜선 자르기

문제

https://www.acmicpc.net/problem/1654

풀이

이분 탐색을 활용한 풀이

랜선의 길이는 2^31-1 == 21억 보다 작거나 같은 자연수이기 때문에
완전 탐색으로 풀면 약 21초 이상으로(python 에서는 8000번 당 1초) 시간 제한인 2초를 넘는다.
이러한 이유로 이분탐색을 사용했다.

이분 탐색의 시간복잡도는

이다.

따라서 최대 31번 연산을 수행한다.

이분 탐색 전 start 값은 1, end는 최대 랜선 길이, mid는 최대 랜선 길이 // 2 로 설정한다.

주어진 랜선들을 각각 mid 값으로 나눈 몫을 더한 값이 목표 랜선 개수보다 작으면
나누는 값(mid)을 감소시켜야 나눈 몫의 합이 커지므로
이분 탐색의 범위 왼쪽 범위로 변경한다.

목표 랜선 개수보다 크거나 혹은 같을 때가 나오는데 이때 이분탐색을 멈춰선 안된다.
이 값이 최대 랜선의 길이가 아닐 수 있기 때문이다.

따라서 나누는 값을 증가시켜서 나눈 몫의 합이 작아지므로
이분 탐색의 범위를 오른쪽 범위로 변경한다.

이 작업을 start > end 일때 까지 반복한다.

import sys

data = sys.stdin.read().strip().split("\n")

def solution(data):
    K, N = map(int, data[0].split(" "))
    lines = []
    min_line, max_line = 1000001, 0
    for i in range(1, K + 1):
        data[i] = int(data[i])
        lines.append(data[i])
        min_line = min(min_line, data[i])
        max_line = max(max_line, data[i])

    start = 1
    end = max_line
    mid = end // 2 if end != 1 else 1
    answer = 0

    while start <= end:
        count = 0
        for line in lines:
            count += line // mid

        if count < N:  # 왼쪽 범위
            end = mid - 1
        else:  # 오른쪽 범위
            answer = max(answer,mid)
            start = mid + 1

        mid = (start + end) // 2

    print(answer)


solution(data)