[자료구조] Binary heap

Binary heap

최대값 또는 최소 값을 빠르게 찾기 위해 고안된
배열 기반의 완전 이진 트리 (마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있는 이진트리)

우선 순위 큐를 구현할때 가장 효율이 좋은 자료구조이다.

종류

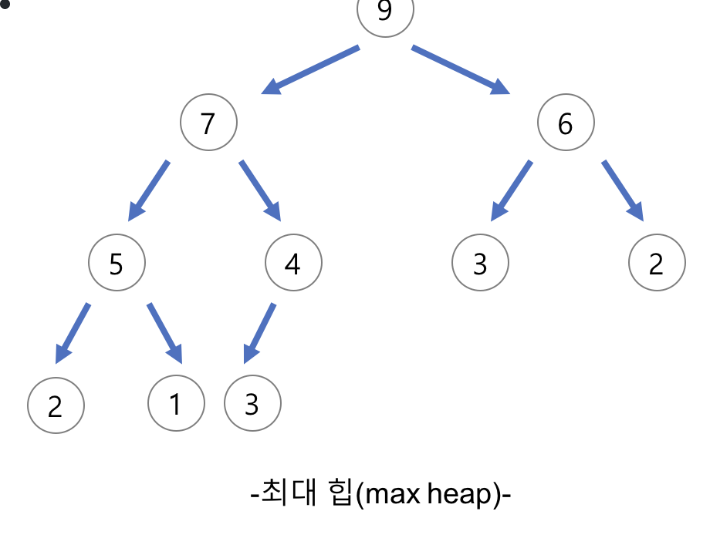
Max Heap

본인 노드의 값이 자식 노드의 값보다 크거나 같은 완전 이진 트리

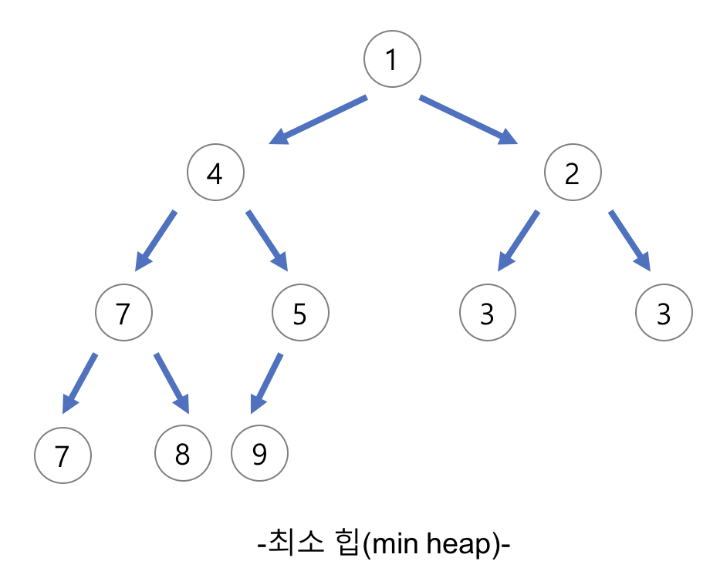
Min Heap

본인 노드의 값이 자식 노드의 값보다 작거나 같은 완전 이진 트리

구현

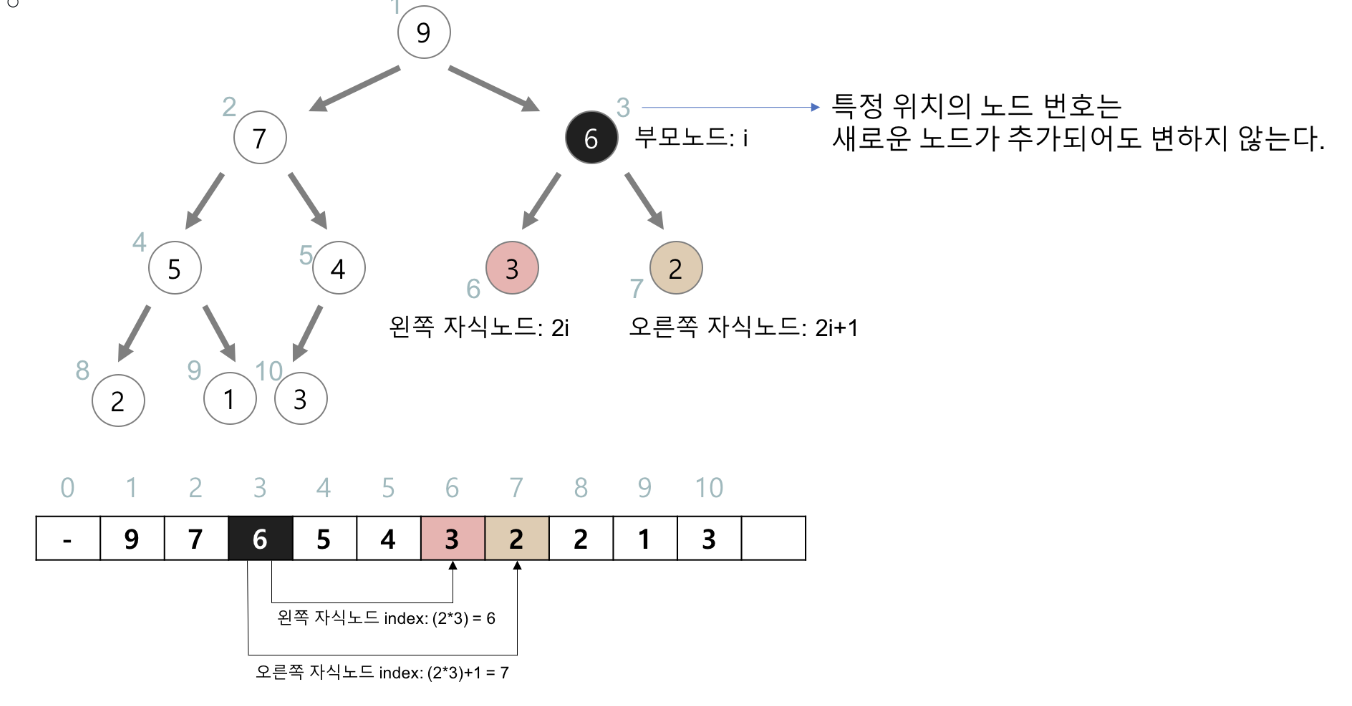
힙을 저장하는 표준적인 자료구조는 배열이다.

• 구현을 쉽게하기 위해서 인덱스 0번은 사용하지 않는다.
• 특정 위치의 노드 번호는 새로운 노드가 추가되어도 변하지 않는다.
  • 예를 들어 루트 노드의 오른쪽 노드의 번호는 항상 3이다.
• 본인 노드와 자식 노드의 관계
  • 왼쪽 자식의 인덱스 -> (본인 노드의 인덱스) * 2
  • 오른쪽 자식의 인덱스 -> (본인 노드의 인덱스) * 2 + 1
  • 본인 노드의 인덱스 -> (자식 노드의 인덱스) / 2
    

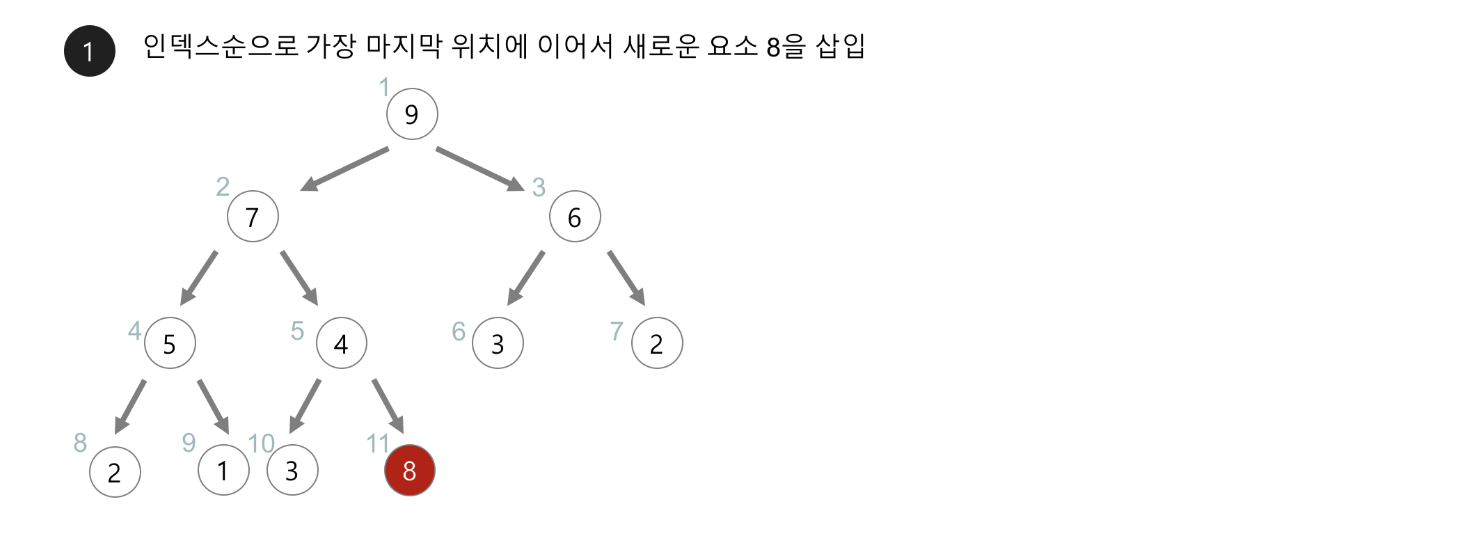
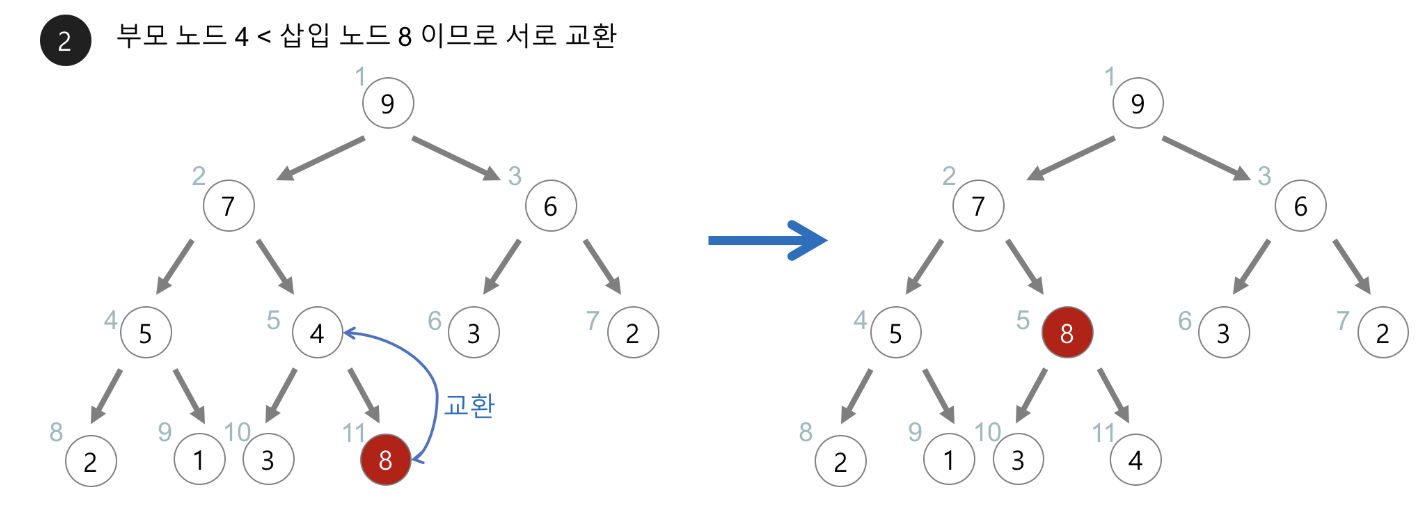
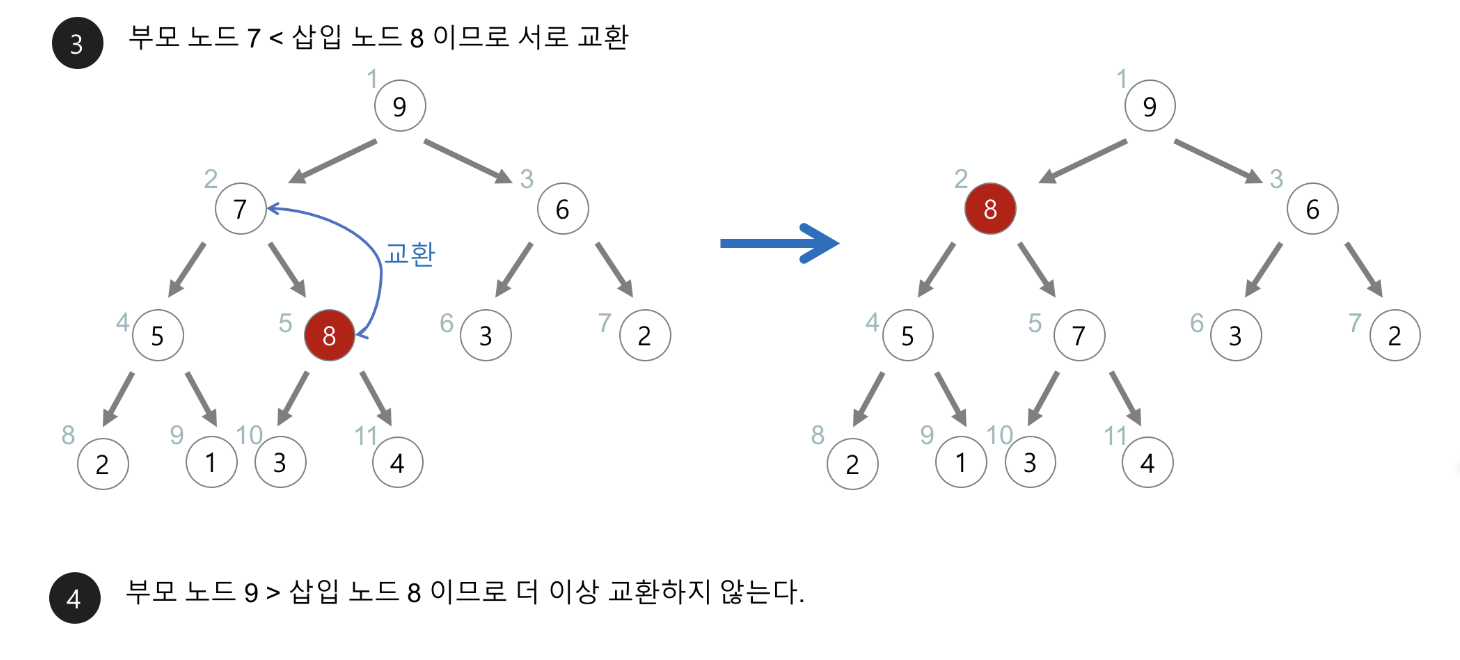
삽입

1. 트리의 마지막 레벨의 가장 오른쪽에 노드를 추가한다.
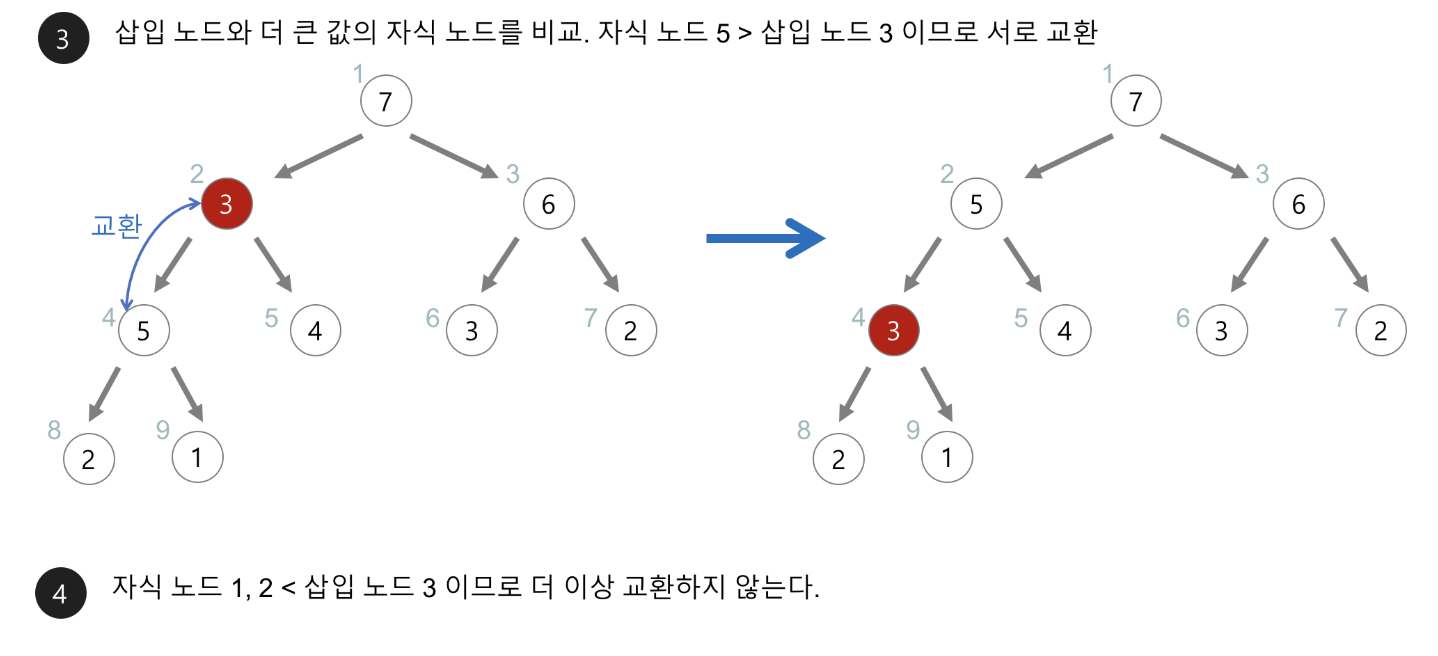
2. 이후 새로 추가된 노드는 부모 노드와 비교하여 자식 노드가 작으면(min)/크면(max)위치를 바꾼다.
3. 이 과정을 루트 노드까지 반복한다.
   

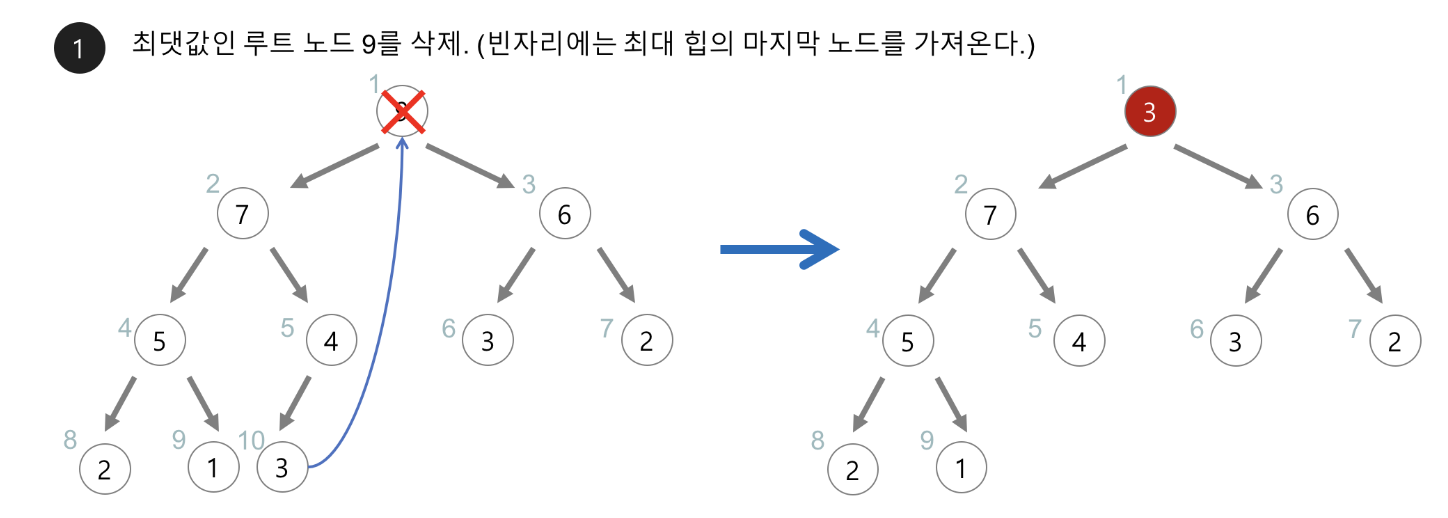
삭제

삭제는 루트 노드를 삭제한다.
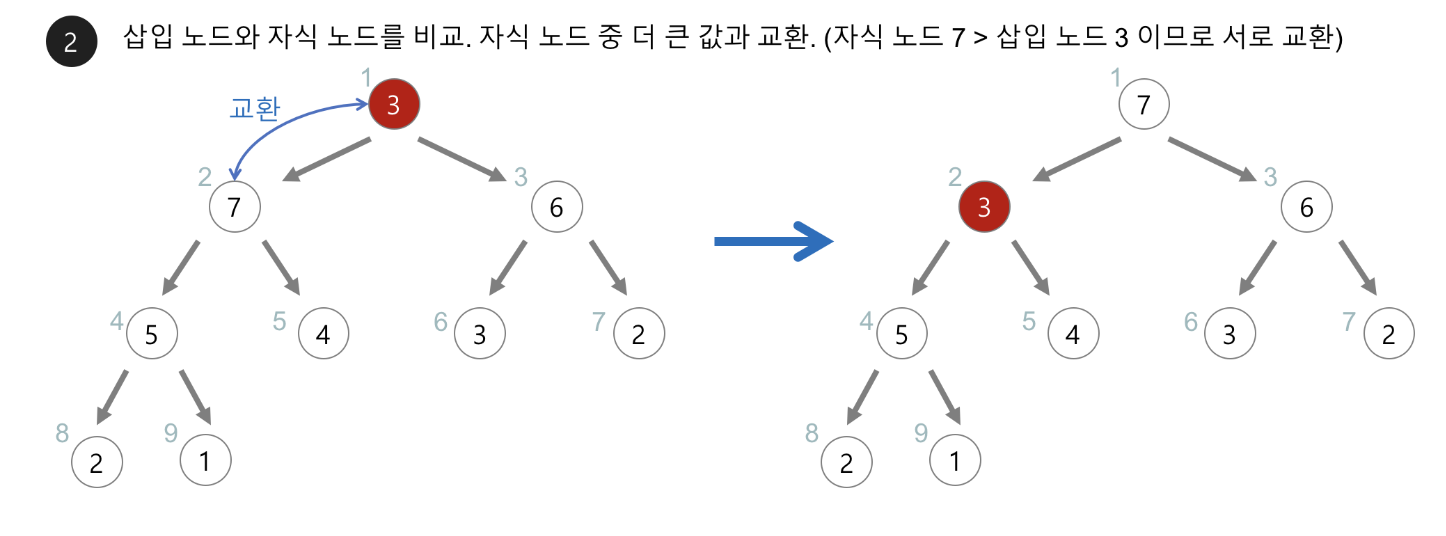
1. 루트 노드를 삭제하고 그 자리는 마지막 노드로 대체한다.
2. 새로운 루트 노드와 자식 노드와 비교하고 자식노드가 더 작으면(min)/크면(max) 위치를 바꾼다.
3. min/max heap의 성질을 만족할 때까지 반복한다.