Tree
계층적 관계를 표현하는 비선형적 자료구조
구조
- 노드 : 트리를 구성하고 있는 각각의 요소
- 엣지 : 노드와 노드를 연결하는 선
- 루트 노드: 최상위 노드
- 단말 노드(leaf node) : 하위에 노드가 연결되어 있지 않은 노드
- 비 단말 노드 : 단말 노드를 제외한 나머지 노드
트리의 종류
이진 트리(Binary tree)
각 노드가 최대 두개의 자식을 갖는 트리
이진 트리 순회법
전위 순회
현재 노드-> 왼쪽 노드 -> 오른쪽 자식 노드
void preOrderTraversal(TreeNode node) {
if(node != null) {
visit(node);
preOrderTraversal(node.left);
preOrderTraversal(node.right);
}
}중위 순회
왼쪽 자식 노드 -> 현재 노드 -> 오른쪽 자식 노드
void preOrderTraversal(TreeNode node) {
if(node != null) {
preOrderTraversal(node.left);
visit(node);
preOrderTraversal(node.right);
}
}후위 순회
왼쪽 자식 노드 -> 오른쪽 자식 노드 -> 현재 노드
void preOrderTraversal(TreeNode node) {
if(node != null) {
preOrderTraversal(node.left);
preOrderTraversal(node.right);
visit(node);
}
}이진 탐색 트리(Binary Search Tree)
모든 노드가 다음과 같은 특정 순서를 따르는 이진 트리
일반적으로 중복 값을 허용하지 않는다.
검색 목적 자료 구조이므로 중복이 많은 경우 트리를 사용하여 속도를 느리게할 필요가 없기 때문
중복이 많다면 다른 자료구조를 사용하던가 노드에 count값을 가지게 하여 처리하는 것이 효율적왼쪽 자손 노드들 <= 본인 노드 < 오른쪽 자손 노드들
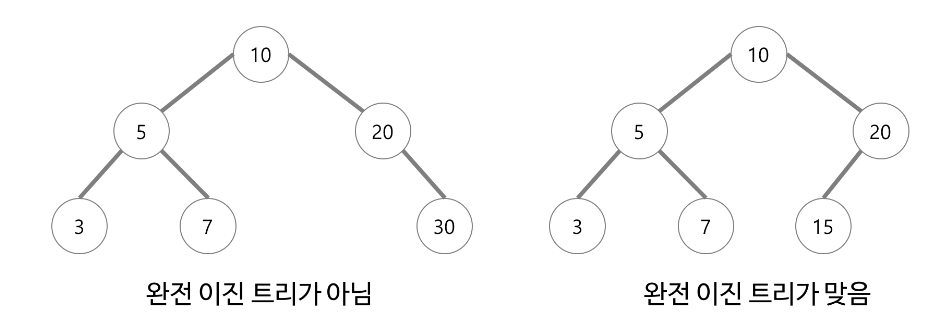
완전 이진 트리(Complete Binary Tree)
마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있는 이진트리
마지막 레벨 h에서는
1 ~ 2h-1개의 노드를 가질 수 있다.
완전 이진 트리는 배열을 사용해 효율적으로 표현이 가능하다.완전 이진 트리는 왼쪽 부터 채워져야한다.
이진 탐색 트리의 평균 시간복잡도는 0(logN) 인데
정렬된 데이터가 들어가면 깊이가 계속 커지기 때문에 O(N)이 된다.이를 발전시킨 트리가 balanced tree 이다.
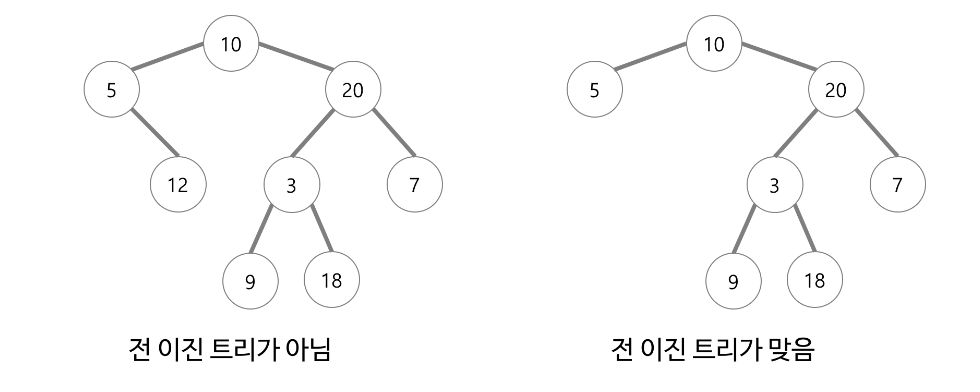
전 이진 트리(Full Binary Tree 또는 Strictly Binary Tree)
모든 노드가 0개 또는 2개의 자식을 같는 이진 트리
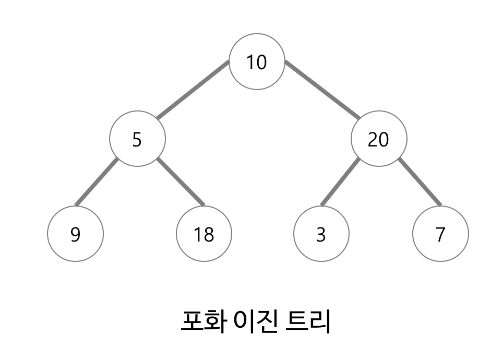
포화 이진 트리(Perfect Binary Tree)
모든 노드가 2개의 자식을 갖는 이진 트리
모든 말단 노드는 같은 높이에 있어야한다.
마지막 단계에서 노드의 개수가 최대가 되어야한다.
노드의 개수는 반드시 2^h - 1 이어야 한다.(h: 트리의 높이)
스패닝 트리
모든 정점을 포함하며 최소한의 간선으로 이뤄진 트리
최소 스패닝 트리
가중치의 합이 최소인 스패닝 트리
최소 스패닝 트리를 구현하는 방법
Kruskal 알고리즘
그래프 간선들을
가중치의 오름차순으로 정렬해 놓은 뒤,
사이클을 형성하지 않는 선에서 정렬된 순서대로 간선을 선택합니다.
prim 알고리즘
임의의 정점을 시작으로 집합에 있는 모든 정점으로부터 뻗어나가는 간선들 중
사이클을 형성하지 않고 가장 가중치가 작은 간선을 선택합니다.
Union-Find 알고리즘
임의의 엣지에서 연결된 엣지들 중 가장 값이 작은 값을 기억하여
서로소인지 판별하는 알고리즘
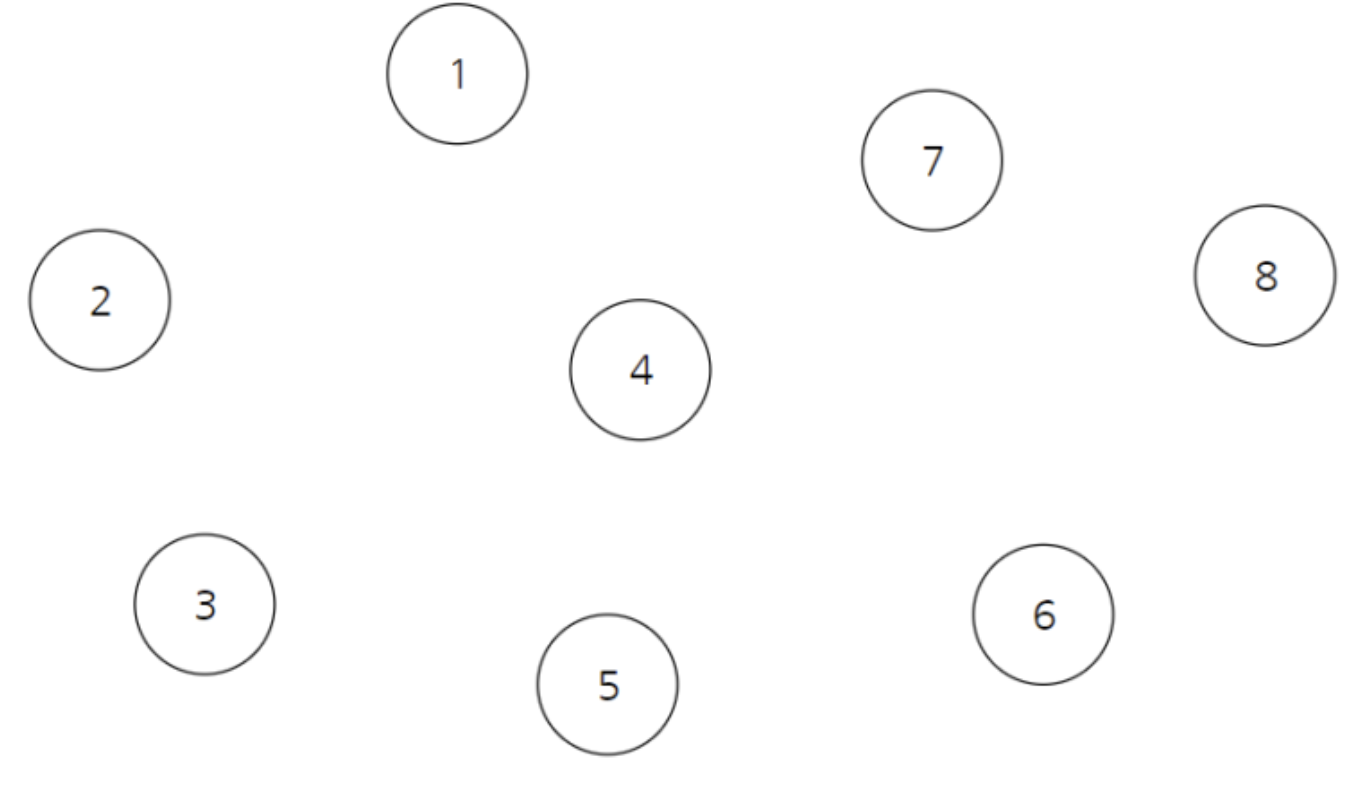
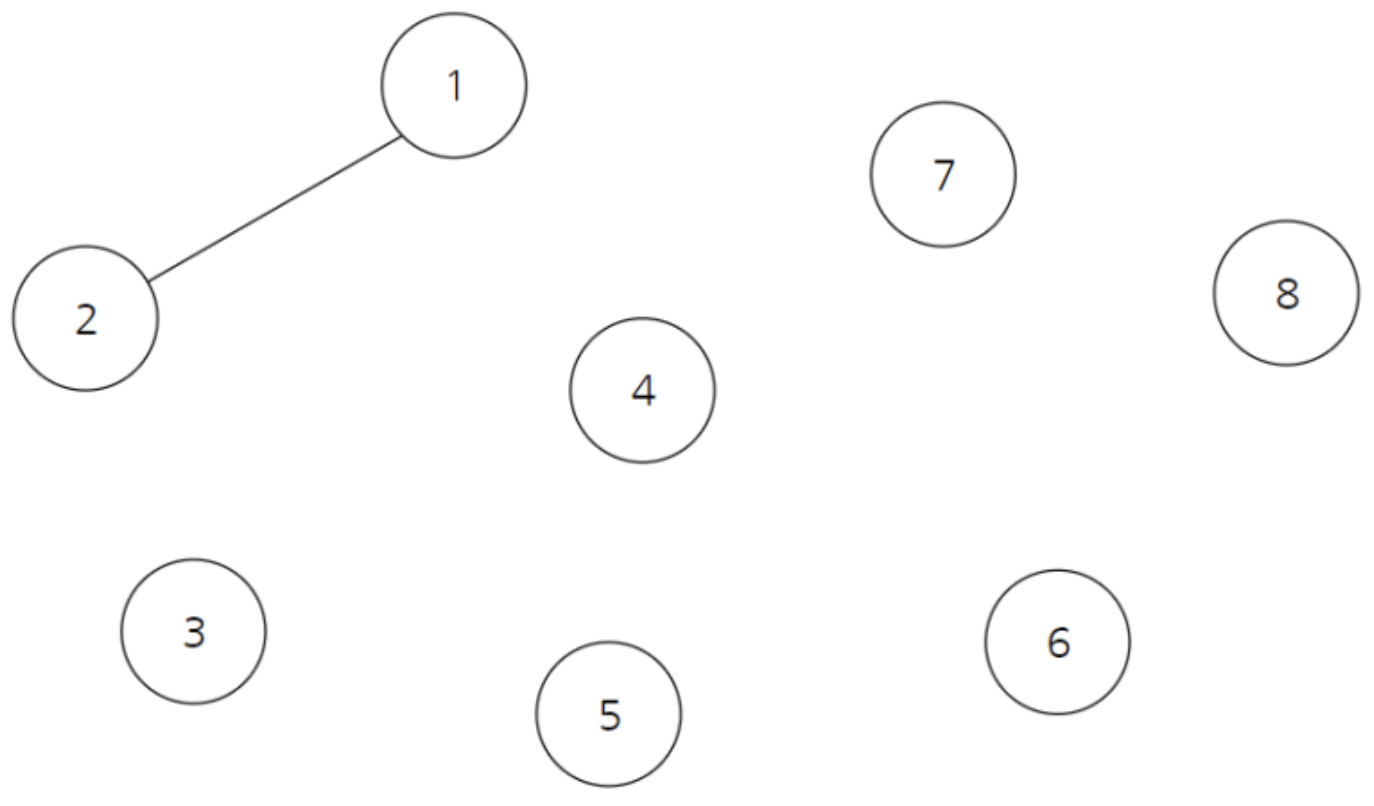
위와 같이 여러개의 노드가 존재하고 있다고 가정하자
현재는 모두 연결되어 있지않고 각자 자신만을 집합의 원소로 가지고 있을 때
모든 값은 자기 자신을 가리키게 한다.
이 때 위와 같이 1과 2가 연결되었다고 가정하면 표는 다음과 같이변경된다.
부모를 재할당할때는 일반적으로 더 작은 값으로 지정한다.
이를Union이라고 한다.
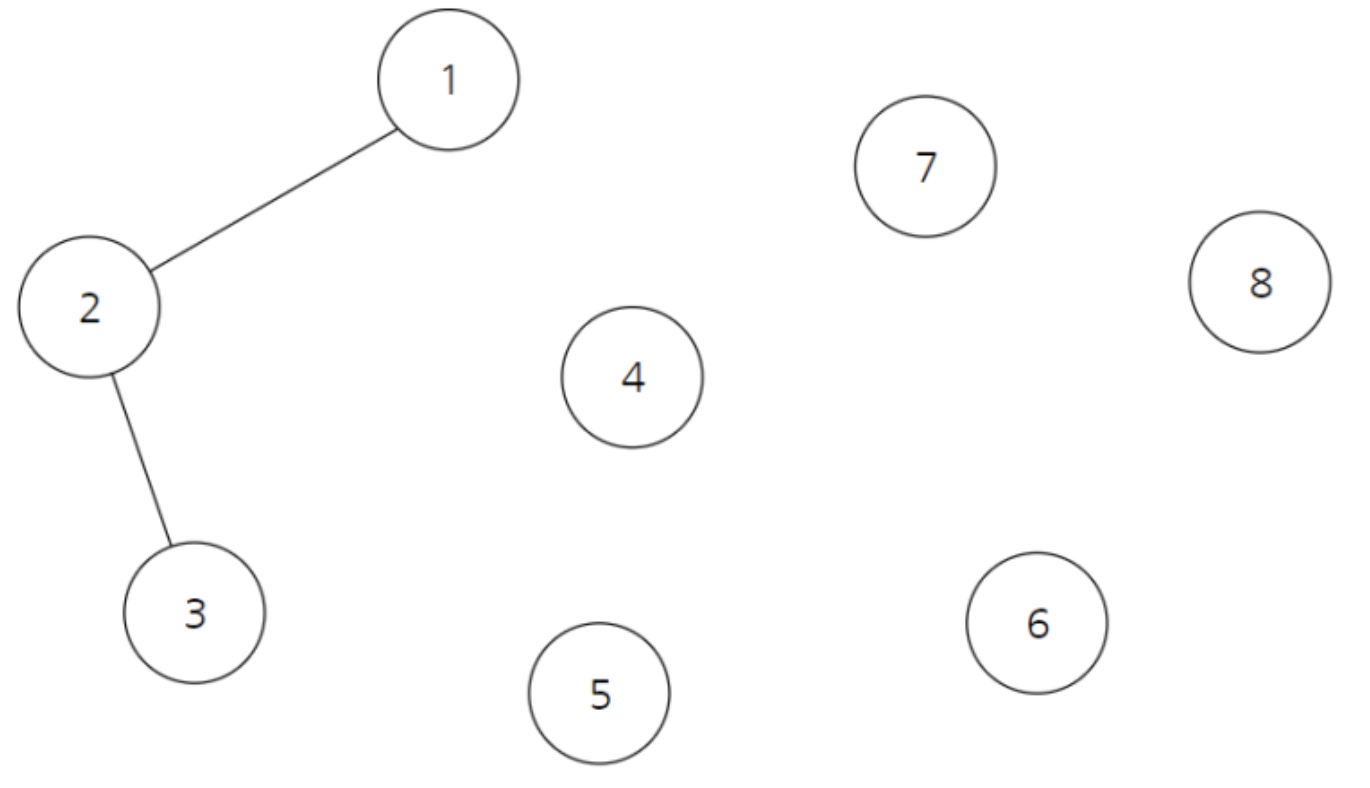
2와 3이 연결된 경우 표는 다음과 같이 변경된다.이때 1과 3이 연결되어있는지 파악하려면 재귀 함수를 사용하면 된다.
해당 노드에서 부모 노드를 탐색하는 작업을 해당노드와 부모노드와 같아질때 까지 진행한다.
이러한 작업을Find라고 한다.
#include <stdio.h>
int getParent(int parent[], int x) {
if(parent[x] == x) return x;
return parent[x] = getParent(parent, parent[x]);
}
// 각 부모 노드를 합칩니다.
void unionParent(int parent[], int a, int b) {
a = getParent(parent, a);
b = getParent(parent, b);
if(a < b) parent[b] = a;
else parent[a] = b;
}
// 같은 부모 노드를 가지는지 확인합니다.
int findParent(int parent[], int a, int b) {
a = getParent(parent, a);
b = getParent(parent, b);
if(a == b) return 1;
else return 0;
}